
| Citation: | Xin He, Changrong Liang, Yang Yang, Guiying Chen, Xiaodong Shang, Xiaozhou He, Penger Tong. Vertical multiple-layer structure of temperature and turbulent diffusivity in the South China Sea[J]. Acta Oceanologica Sinica, 2022, 41(10): 14-21. doi: 10.1007/s13131-022-2005-5 |
The South China Sea (SCS) covers a region from the equator to 23°N and from 99°E to 121°E with an average depth about 1 212 m. It is one of the largest tropical marginal seas on earth. It has a deep basin surrounded by a steep continental slope and connects to the East China Sea via the Taiwan Strait, to the western Pacific Ocean via the Luzon Strait, to the Sulu Sea via the Mindoro Strait, and to the Java Sea via the Karimata Strait.
A widely accepted notion is that the SCS has a unique, three-layer cyclonic-anticyclonic-cyclonic (CAC) circulation pattern. Upper-layer circulation in the SCS has been widely studied since the first report by Wyrtki (1961). The results of the Princeton Ocean Model suggests that seasonal upper-layer circulation patterns and upwelling phenomena are determined and forced by the wind, while the lateral boundary forcing plays a secondary role in determining the magnitude of circulation velocities (Chu et al., 1999). Principal component analysis of altimeter data shows that sea-level variation consists mainly of two modes, corresponding well to the first two modes of the wind stress curl. Mode 1 represents oscillation in the southern basin and shows little inter-annual variation, and Mode 2 represents weak oscillation in the southern basin and strong oscillation off the coast of central Vietnam (Shaw et al., 1999). It is thus concluded that, as a result of the seasonally reversed monsoon, upper circulation exhibits distinct seasonal variability with cyclonic circulation over the whole SCS basin in winter, cyclonic circulation in the northern half of the basin, and anticyclonic circulation in the southern half of the basin in summer (Hu et al., 2000; Liu et al., 2001; Su, 2004).
By contrast, middle- and deep-layer SCS circulation follows anticyclonic and cyclonic patterns, respectively (Lan et al., 2013). The results of a numerical experiment show that the basin circulation of the SCS is cyclonic gyres at the surface and in the abyss, but an anti-cyclonic gyre at intermediate depths (Yuan, 2002). This suggests that the SCS plays the role of a “mixing mill” that mixes the surface and deep waters to return them to the Luzon Strait at intermediate depths. An analysis of updated monthly climatology of observed temperature and salinity from the U.S. Navy Generalized Digital Environment Model revealed that basin-scale cyclonic circulation lies over the deep SCS, and that the boundary current transport of the cyclonic circulation is around 3.0×106 m3/s, supporting speculation that the overflow of the Luzon Strait provides a source for the basin-scale deep SCS cyclonic gyre (Wang et al., 2011). Based on these studies, CAC circulation patterns in the upper, middle, and deep layers of the SCS have been suggested, although the depth range of each layer differs among studies (Gan et al., 2016).
A critical issue for understanding the vertical structure of circulation is the physical mechanism for maintaining the structure. Vertical motion induced by mixing is considered as the primary driving mechanism of the transformation of deep water in the deep SCS (Xie et al., 2013; Lan et al., 2013). By analyzing the potential density, potential vorticity, dissolved oxygen, and sediment distribution in the deep SCS, previous studies found that deep water in the SCS has similar characteristics to Pacific water at ~2000 m depth which implies that SCS deep water comes from deep northwestern Pacific via the Luzon Strait (Li and Qu, 2006; Qu et al., 2006). The enhanced diapycnal diffusivity in the SCS is about O(10−3 m2/s) below 1000 m and reaches O(10−2 m2/s) in the Luzon Strait below 500 m (Tian et al., 2009). This suggests that intensified diapycnal mixing might be responsible for the transformation of deep water. Strong diffusivity in the SCS also enhances SCS water transformation by itself in the vertical direction (Shu et al., 2014). However, we still do not clearly understand the overall vertical structure of circulation and the physical mechanism for maintaining this vertical structure.
In this study, we revealed the vertical turbulence structure of the SCS and identify the depth range of each layer using the observed turbulent diffusivity
The rest of the paper is organized as follows. In-situ data are introduced in Section 2. The depths of the water layers are presented in Section 3. Section 4 provides discussion of each water layer, and Section 5 offers conclusions.
Figure 1 shows a sketch of the SCS landscape, together with the locations of the observation stations. The field data were measured using three different instruments: the Sea-Bird Electronic 911 Plus CTD, the Turbulence Ocean Microstructure Acquisition Profiler (TurboMAP, Wolk et al., 2002), and the Vertical Microstructure Profiler-Expendable (VMP-X, Shang et al., 2017b).

At Stas c1–c9, we used VMP-X to measure the whole profile of turbulent velocity shear (
| $$ \varepsilon =7.5\nu \left\langle{{\left(\partial u/\partial z\right)}^{2}}\right\rangle , $$ | (1) |
where
| $$ {\kappa }_{\rho }=\varGamma \varepsilon /{N}^{2} , $$ | (2) |
where
In addition to measurements of (
Figure 3a shows the obtained

Figure 3b shows the evolution of the probability density function (PDF)
In order to improve the accuracy, we calculated the weighted average value of
| $$ {\rm{\delta}} {\kappa }_{\rho }=\left({{\rm{log}}}_{10}{\kappa }_{\rho }-{{\rm{log}}}_{10}{\kappa }_{\min}\right)/\left({{\rm{log}}}_{10}{\kappa }_{\max}-{{\rm{log}}}_{10}{\kappa }_{\min}\right) , $$ | (3) |
where
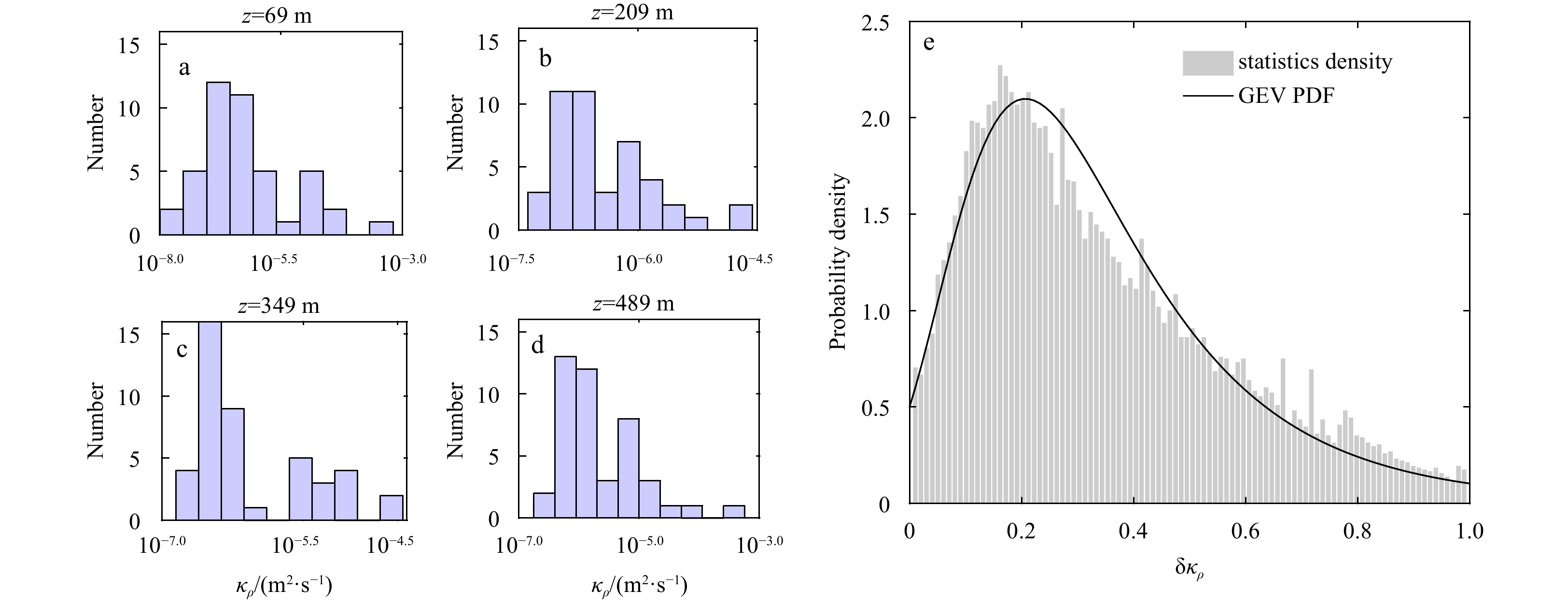
| $$ \begin{split}P\left({\rm{\delta}} {\kappa }_{\rho }\right)=&\frac{1}{\sigma }\exp\left\{-{\left[1+\frac{\text{γ} \left({\rm{\delta}} {\kappa }_{\rho }-\mu \right)}{\sigma }\right]}^{-\frac{1}{\text{γ} }}\right\}\times\\ &{\left\{{\left[1+\frac{\text{γ} \left(\delta {\kappa }_{\rho }-\mu \right)}{\sigma }\right]}^{-\frac{1}{\text{γ} }}\right\}}^{-1-\frac{1}{\text{γ} }} ,\end{split} $$ | (4) |
where
The GEV distribution is often used to model the smallest or largest value among a large set of independent, identically distributed random values representing measurements or observations. It indicates that each value of
Figure 5a shows the probability density function (PDF)
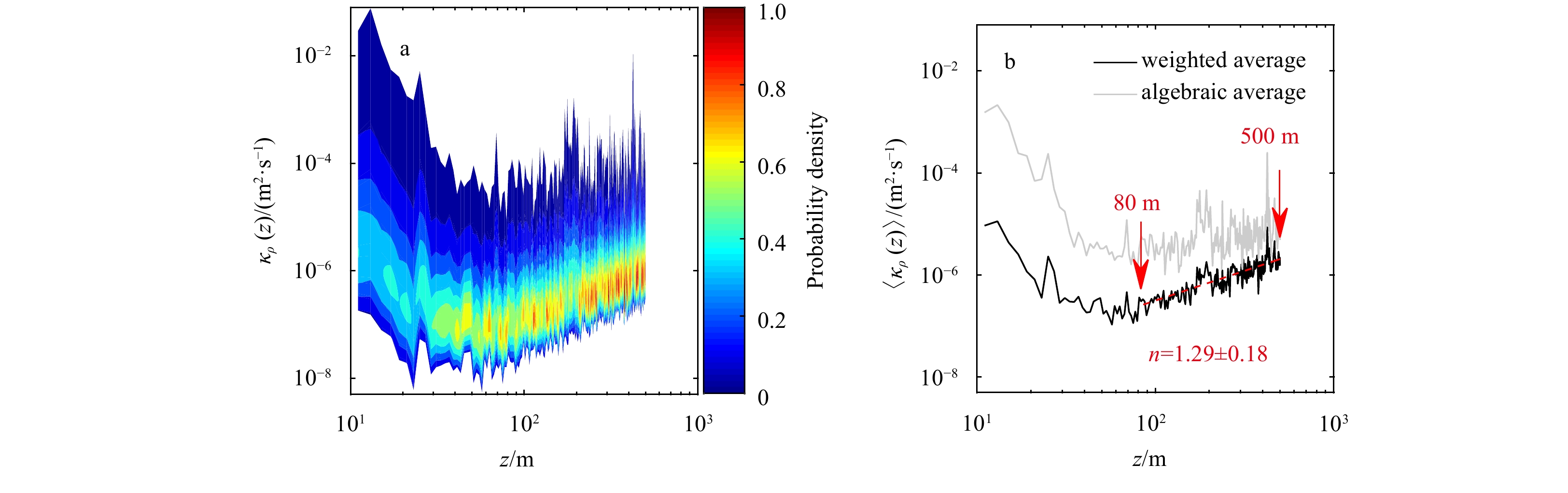
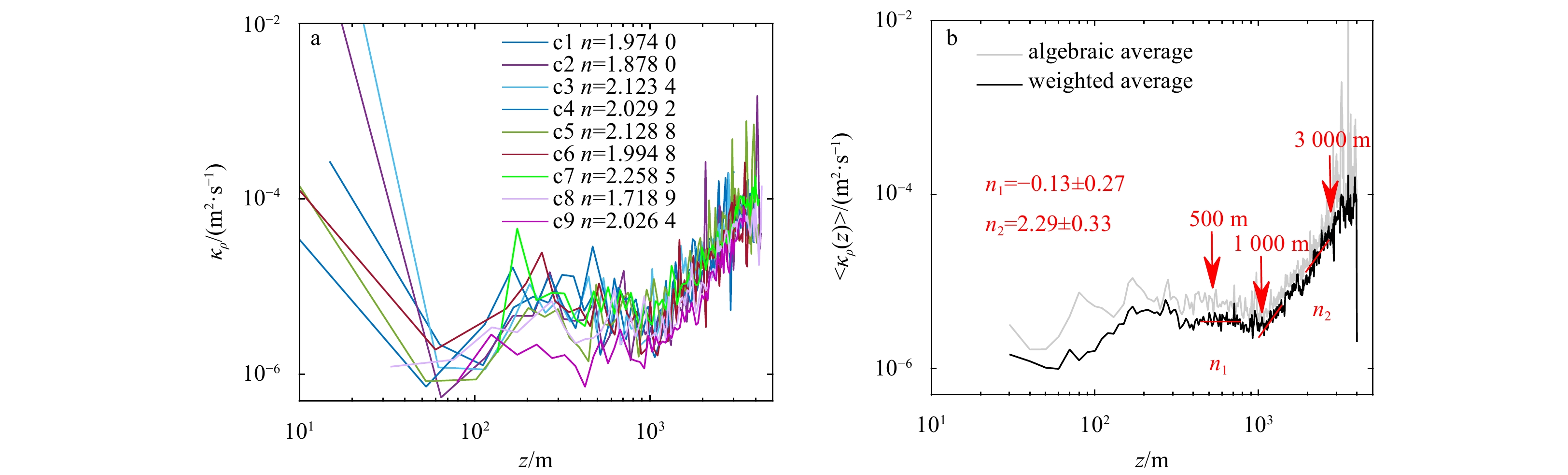
Figure 6a shows the vertical profile
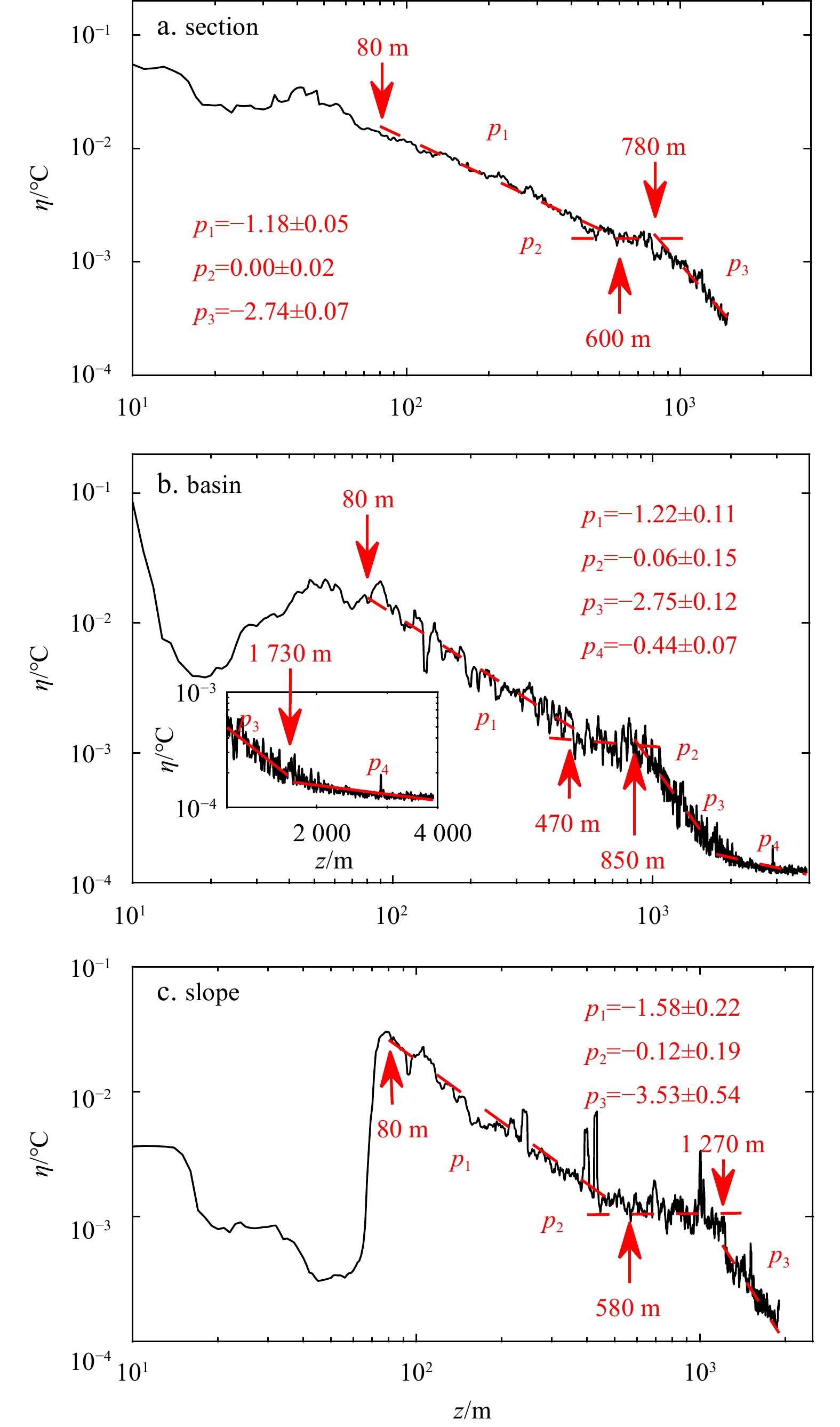
Similar multiple-layer scaling regimes are also observed from the root mean square of temperature fluctuation:
| $$ \eta \left(z\right)=\sqrt{\frac{\displaystyle\sum _{i=1}^{K}{\Big({T}_{i}- \bar{T}\Big)}^{2}}{K}}, $$ | (5) |
where
| Area or source | ZS of water layer/m | |||
| UL | TL | ML | DL | |
| Section of 18°N | 80−600 | 600−780 | 780 to NAN | NAN |
| Central basin in the SCS | 65−470 | 470−850 | 850−1730 | 1730 to NAN |
| Slope of the northern SCS | 80−580 | 580−1270 | 1270 to NAN | NAN |
| $ \left\langle{{\mathit{\kappa }}_{\mathit{\rho }}\left(\mathit{z}\right)}\right\rangle $ | 80−500 | 500−1000 | 1000 to NAN | NAN |
| Model (Gan et al., 2016) | 0−750 | NAN | 750−1500 | 1500 to NAN |
| Note: NAN means no data. UL: upper layer, TL: transition layer, ML: middle layer, and DL: deep layer. | ||||
The measured
Through in-situ turbulence and temperature data, we revealed the multiple-layer structure of the SCS. The results prompt more questions, however, especially regarding the TL, which to our knowledge has not been mentioned in earlier studies.
The salient feature of TL is that
| $$ {\left\langle{v'\theta '}\right\rangle}_{t}\equiv -{\kappa }_{t}\frac{\partial T}{\partial {{{z}}}}, $$ | (6) |
where
| $$ {w}_{0}\frac{\partial T}{\partial z}=\frac{\partial }{\partial z}\left({\kappa }_{t}\frac{\partial T}{\partial z}\right) , $$ | (7) |
with constants
| $$ T\left(z\right)\propto \mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{z}{{\kappa }_{t}/{w}_{0}}\right) . $$ | (8) |
Figures 8a–c show the temperature profiles
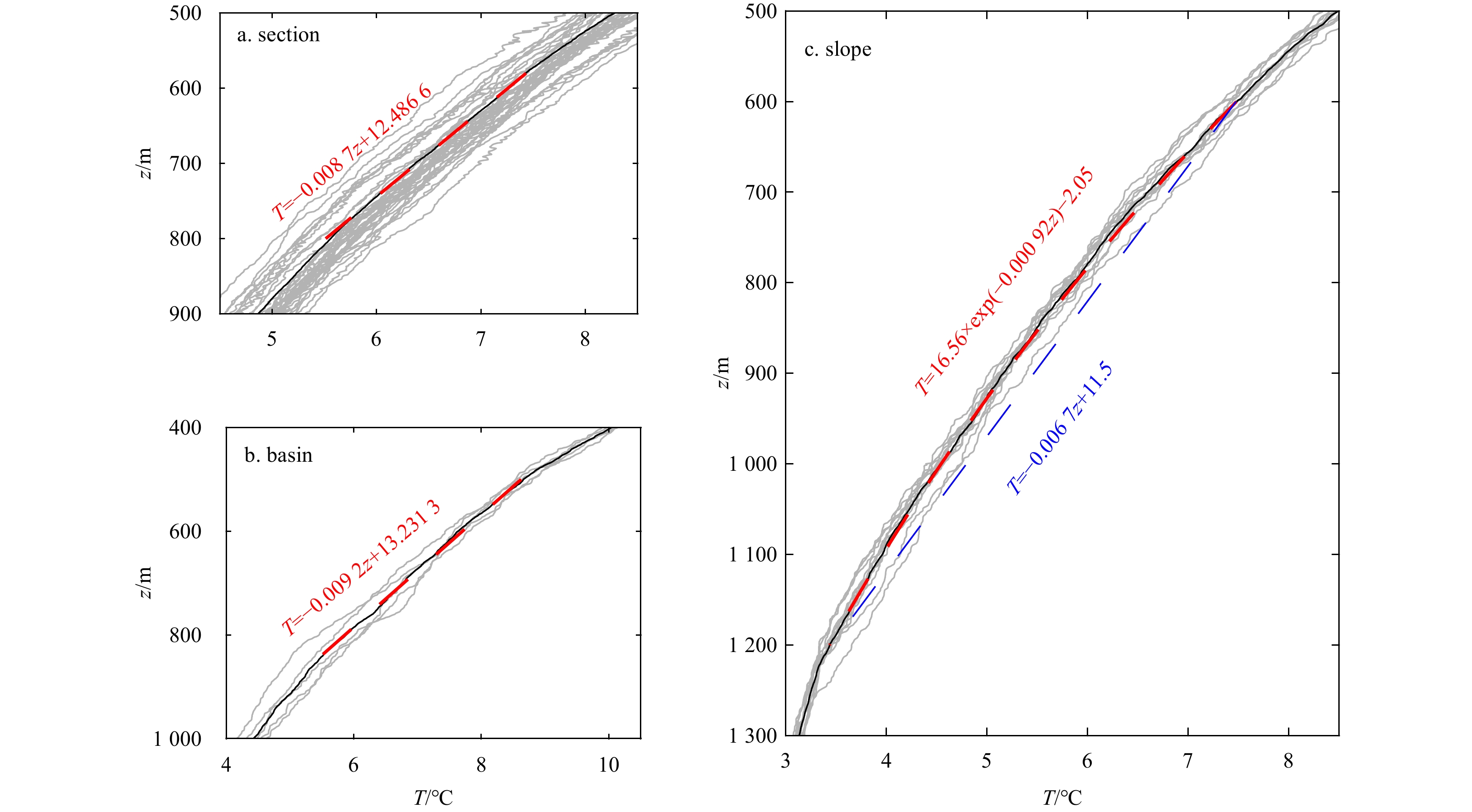
The thickness of the TL is roughly 300 m and the current in the TL is weak in these areas where the sea bottom topography is smooth. As such, it was difficult to distinguish the TL in the earlier studies. Now, we can distinguish the TL by the root mean square of temperature fluctuations
Only in the slope, the profile
Kitaigorodskii and Miropolskii (1970) were the first to describe the vertical temperature structure of an active oceanic layer by means of a self-similarity function that can be expressed as the functional dependence between the dimensionless temperature and depth as follows:
| $$ \frac{{T}_{S}-T}{{T}_{S}-{T}_{D}}={T}\,^{\mathrm{*}}\left(\frac{z-{h}_{S}}{{h}_{D}-{h}_{S}}\right) ,{h}_{S}\leqslant z\leqslant {h}_{D}, $$ | (9) |
where
In earlier studies that only considered the self-similarity function of the active oceanic layer, the conception of multiple layers was not acknowledged. To eliminate the effect of multiple layers, we calculate the dimensionless temperature
| Region | Water layer | Parameter | |
| $ \Delta \mathit{T} $/°C | $ {\mathit{L}}_{\mathit{\lambda }} $/m | ||
| Section of 18°N | UL | 26.9 | 330 |
| ML | 4.4 | 618 | |
| Central basin in the SCS | UL | 27.8 | 234 |
| ML | 3.8 | 541 | |
| Slope of the northern SCS | DL | 0.5 | 645 |
| UL | 29.8 | 175 | |
| ML | 0.9 | 394 | |
Figures 9 and 10 show the
Interestingly, the function of the basin DL is consistent with the function of ML, but the function of the slope ML is slightly different. In the ML of the slope, the temperature profile can be affected by strong bottom friction from the steep continental slope. Moreover, there is no more external influence in the DL of basin, as with the ML of the basin and section. This might also be the reason that turbulent diffusivity
Thus, we proposed that there is one constant function of the dimensionless temperature profile in water layers that have identical turbulence conditions. The rough bottom topography affects the turbulence of the entire water layer. In future studies, the distribution of adjusted parameters can be obtained from abundant temperature data, which will help us to understanding the structure of circulation in the SCS more explicitly.
Using observations, we identified the multiple-layer structure of the SCS to better understand its circulation pattern. In earlier studies, the vertical structure of circulation was explored from velocity field, although this is challenging with field measurements of the real ocean (Tian et al., 2006, 2009; Lan et al., 2013; Gan et al., 2016). In this study,
Our study of the multiple-layer structure provides a further improvement over previous theoretical methods. The solution of the temperature profile by Munk (1966) is useful for calculating the vertical velocity of real ocean areas, like steep continental slopes, which have a thick transition layer with constant turbulent diffusivity. Furthermore, the self-similarity function provides a profitable tool for supervising turbulence exclusively using a dimensionless temperature profile.
Considering the inadequate observations, more research is needed to verify our conclusions. Although this was a preliminary study, it improves our understanding of the vertical multiple-layer structure of the SCS. In particular, it will be crucial for exploring the physical mechanism for maintaining the temperature structure.
|
Chu P C, Edmons N L, Fan Chenwu. 1999. Dynamical mechanisms for the South China Sea seasonal circulation and thermohaline variabilities. Journal of Physical Oceanography, 29(11): 2971–2989. doi: 10.1175/1520-0485(1999)029<2971:DMFTSC>2.0.CO;2
|
|
Gan Jianping, Liu Zhiqiang, Hui C R. 2016. A three-layer alternating spinning circulation in the South China Sea. Journal of Physical Oceanography, 46(8): 2309–2315. doi: 10.1175/JPO-D-16-0044.1
|
|
Golosov S, Zverev I, Shipunova E, et al. 2018. Modified parameterization of the vertical water temperature profile in the FLake model. Tellus A: Dynamic Meteorology and Oceanography, 70(1): 1–7
|
|
Hu Jianyu, Kawamura H, Hong Huasheng, et al. 2000. A review on the currents in the South China Sea: Seasonal circulation, South China Sea Warm Current and Kuroshio Intrusion. Journal of Oceanography, 56(6): 607–624. doi: 10.1023/A:1011117531252
|
|
Kitaigorodskii S A, Miropolskii Y Z. 1970. On the theory of active layer of open ocean. Atmospheric and Oceanic Physics, 6(2): 97–102
|
|
Lan Jian, Zhang Ningning, Wang Yu. 2013. On the dynamics of the South China Sea deep circulation. Journal of Geophysical Research, 118(3): 1206–1210. doi: 10.1002/jgrc.20104
|
|
Li Li, Qu Tangdong. 2006. Thermohaline circulation in the deep South China Sea basin inferred from oxygen distributions. Journal of Geophysical Research, 111(C5): C05017. doi: 10.1029/2005JC003164
|
|
Liang Changrong, Chen Guiying, Shang Xiaodong. 2017. Observations of the turbulent kinetic energy dissipation rate in the upper central South China Sea. Ocean Dynamics, 67(5): 597–609. doi: 10.1007/s10236-017-1051-6
|
|
Liu Qinyu, Yang Haijun, Liu Zhengyu. 2001. Seasonal features of the Sverdrup circulation in the South China Sea. Progress in Natural Science, 11(3): 202–206
|
|
Munk W H. 1966. Abyssal recipes. Deep-Sea Research and Oceanographic Abstracts, 13(4): 707–730. doi: 10.1016/0011-7471(66)90602-4
|
|
Osborn T R. 1980. Estimates of the local rate of vertical diffusion from dissipation measurements. Journal of Physical Oceanography, 10(1): 83–89. doi: 10.1175/1520-0485(1980)010<0083:EOTLRO>2.0.CO;2
|
|
Qu Tangdong, Girton J B, Whitehead J A. 2006. Deepwater overflow through Luzon Strait. Journal of Geophysical Research, 111(C1): C01002. doi: 10.1029/2005JC003139
|
|
Shang Xiaodong, Liang Changrong, Chen Guiying. 2017a. Spatial distribution of turbulent mixing in the upper ocean of the South China Sea. Ocean Science, 13(3): 503–519. doi: 10.5194/os-13-503-2017
|
|
Shang Xiaodong, Qi Yongfeng, Chen Guiying, et al. 2017b. An expendable microstructure profiler for deep ocean measurements. Journal of Atmospheric and Oceanic Technology, 34(1): 153–165. doi: 10.1175/JTECH-D-16-0083.1
|
|
Shaw P T, Chao S Y, Fu L L. 1999. Sea surface height variations in the South China Sea from satellite altimetry. Oceanologica Acta, 22(1): 1–17. doi: 10.1016/S0399-1784(99)80028-0
|
|
Shu Yeqiang, Xue Huijie, Wang Dongxiao, et al. 2014. Meridional overturning circulation in the South China Sea envisioned from the high-resolution global reanalysis data GLBa0.08. Journal of Geophysical Research, 119(5): 3012–3028. doi: 10.1002/2013JC009583
|
|
Su Jilan. 2004. Overview of the South China Sea circulation and its influence on the coastal physical oceanography outside the Pearl River Estuary. Continental Shelf Research, 24(16): 1745–1760. doi: 10.1016/j.csr.2004.06.005
|
|
Thorpe S A. 2005. The measurement of turbulence and mixing. In: Thorpe S A, ed. The Turbulent Ocean. Cambridge, UK: Cambridge University Press, 172–189
|
|
Tian Jiwei, Yang Qingxuan, Liang Xinfeng, et al. 2006. Observation of Luzon Strait transport. Geophysical Research Letters, 33(19): L19607. doi: 10.1029/2006GL026272
|
|
Tian Jiwei, Yang Qingxuan, Zhao Wei. 2009. Enhanced diapycnal mixing in the South China Sea. Journal of Physical Oceanography, 39(12): 3191–3203. doi: 10.1175/2009JPO3899.1
|
|
Wang Guihua, Xie Shangping, Qu Tangdong, et al. 2011. Deep South China Sea circulation. Geophysical Research Letters, 38(5): L05601. doi: 10.1029/2010GL046626
|
|
Wolk F, Yamazaki H, Seuront L, et al. 2002. A new free-fall profiler for measuring biophysical microstructure. Journal of Atmospheric and Oceanic Technology, 19(5): 780–793. doi: 10.1175/1520-0426(2002)019<0780:ANFFPF>2.0.CO;2
|
|
Wyrtki Klaus. 1961. Physical oceanography of the Southeast Asian waters: scientific results of marine investigations of the South China Sea and the Gulf of Thailand 1959–1961. NAGA Report, 2: 195. doi: 10.1530/jrf.0.0020195
|
|
Xie Qiang, Xiao Jingen, Wang Dongxiao, et al. 2013. Analysis of deep-layer and bottom circulations in the South China Sea based on eight quasi-global ocean model outputs. Chinese Science Bulletin, 58(32): 4000–4011. doi: 10.1007/s11434-013-5791-5
|
|
Yuan Dongliang. 2002. A numerical study of the South China Sea deep circulation and its relation to the Luzon Strait transport. Acta Oceanologica Sinica, 21(2): 187–202
|

| Area or source | ZS of water layer/m | |||
| UL | TL | ML | DL | |
| Section of 18°N | 80−600 | 600−780 | 780 to NAN | NAN |
| Central basin in the SCS | 65−470 | 470−850 | 850−1730 | 1730 to NAN |
| Slope of the northern SCS | 80−580 | 580−1270 | 1270 to NAN | NAN |
| $ \left\langle{{\mathit{\kappa }}_{\mathit{\rho }}\left(\mathit{z}\right)}\right\rangle $ | 80−500 | 500−1000 | 1000 to NAN | NAN |
| Model (Gan et al., 2016) | 0−750 | NAN | 750−1500 | 1500 to NAN |
| Note: NAN means no data. UL: upper layer, TL: transition layer, ML: middle layer, and DL: deep layer. | ||||
| Region | Water layer | Parameter | |
| $ \Delta \mathit{T} $/°C | $ {\mathit{L}}_{\mathit{\lambda }} $/m | ||
| Section of 18°N | UL | 26.9 | 330 |
| ML | 4.4 | 618 | |
| Central basin in the SCS | UL | 27.8 | 234 |
| ML | 3.8 | 541 | |
| Slope of the northern SCS | DL | 0.5 | 645 |
| UL | 29.8 | 175 | |
| ML | 0.9 | 394 | |
| Area or source | ZS of water layer/m | |||
| UL | TL | ML | DL | |
| Section of 18°N | 80−600 | 600−780 | 780 to NAN | NAN |
| Central basin in the SCS | 65−470 | 470−850 | 850−1730 | 1730 to NAN |
| Slope of the northern SCS | 80−580 | 580−1270 | 1270 to NAN | NAN |
| $ \left\langle{{\mathit{\kappa }}_{\mathit{\rho }}\left(\mathit{z}\right)}\right\rangle $ | 80−500 | 500−1000 | 1000 to NAN | NAN |
| Model (Gan et al., 2016) | 0−750 | NAN | 750−1500 | 1500 to NAN |
| Note: NAN means no data. UL: upper layer, TL: transition layer, ML: middle layer, and DL: deep layer. | ||||
| Region | Water layer | Parameter | |
| $ \Delta \mathit{T} $/°C | $ {\mathit{L}}_{\mathit{\lambda }} $/m | ||
| Section of 18°N | UL | 26.9 | 330 |
| ML | 4.4 | 618 | |
| Central basin in the SCS | UL | 27.8 | 234 |
| ML | 3.8 | 541 | |
| Slope of the northern SCS | DL | 0.5 | 645 |
| UL | 29.8 | 175 | |
| ML | 0.9 | 394 | |