| Citation: | Fang Hou, Zhiyi Gao, Jianguo Li, Fujiang Yu. An efficient algorithm for generating a spherical multiple-cell grid[J]. Acta Oceanologica Sinica, 2022, 41(5): 41-50. doi: 10.1007/s13131-021-1947-3 |
In an operational wave forecasting model, in addition to the accuracy, the computational efficiency also needs to be considered. If nearshore wave forecasting is involved, the model should also have a high enough resolution to resolve a complicated coastline and small islands. To improve the resolution of a model under the limitation of computing resources, one-way or two-way nesting, triangular grids, adaptive grids and other technologies have been developed (Chawla et al., 2013; Hsu et al., 2005; Qi et al., 2009, Popinet et al., 2010). Consequently, these technologies also bring about some new problems, such as complex nested structures, cumbersome pre- and pos-tprocessing, and time step limitations due to the minimum size of the grid. Li (2011) developed a spherical multiple-cell (SMC) grid; its variable resolutions, concise advection schemes (Li, 2008) and its support of sub-timesteps for refined cells alleviate the conflicts between computational efficiency and resolution. In addition, by merging longitudinal cells towards the poles as in the reduced grid (Rasch, 1994), the SMC grid can be extended to cover the polar region (Li, 2012). These features make the SMC grid an ideal candidate for operational wave forecasting models.
Validations with satellite and buoy observations show that the SMC grid wave model performs as well as the conventional latitude–longitude grid model and yields better swell predictions if coastlines and small islands are resolved at a refined resolution (Li, 2012). The UK Met Office has implemented a 4-level SMC grid to perform routine ocean surface wave forecasting since October 2016 (Li and Saulter, 2014). Bunney and Saulter (2015) implemented a 3-level SMC grid to establish an ensemble forecast system for the prediction of Atlantic–UK wind waves, and the results were verified by in situ platform data and remotely sensed altimeter data. SMC grids are also used by other research institutions for Arctic wave climate studies (Casas-Prat et al., 2018; Li et al., 2019).
However, the lack of grid generation tools limits the development of SMC grids. WAVEWATCH III provides an IDL program to generate an SMC grid at a global resolution of 50 km without grid refinement. The Met Office provides a program to generate a global 4-level nearshore refined SMC grid. However, the level of refinement in this grid cannot be changed. Durrant and Saulter released a toolkit on GitHub (
To generate an SMC grid with a complex structure more effectively, this paper develops a new algorithm that can not only generate a nearshore refined SMC grid at any level but can also refine the grid in arbitrary areas.
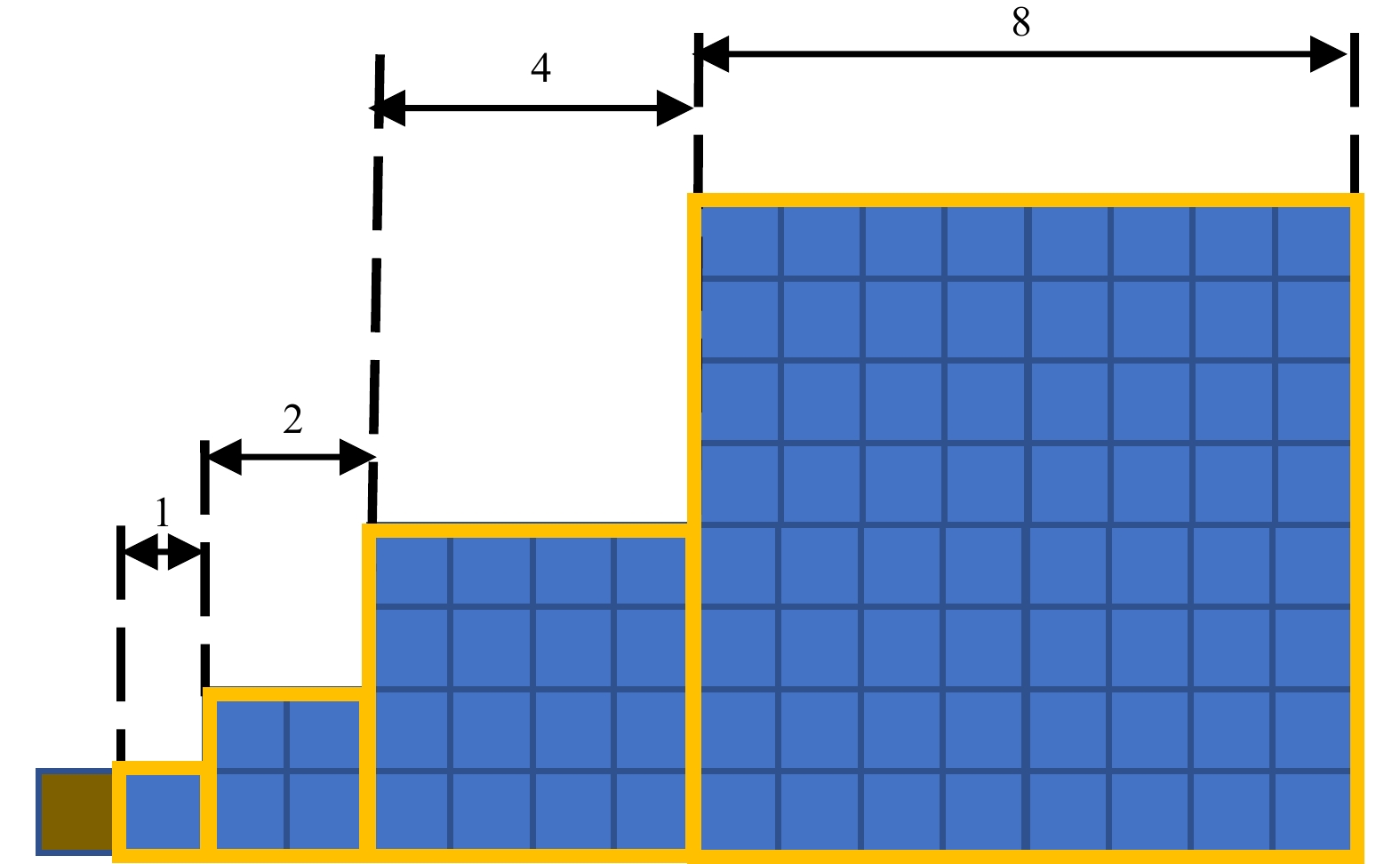
Before the introduction of the algorithm, we need to clarify the naming method of the grid. In this paper, we define the minimum side length of the grid as 1 and the side length of the N-level grid as 2n−1. Thus, the 4-level SMC grid is composed of four grid levels with side lengths of 1, 2, 4, and 8. The largest grid is also called the base grid (as named in WAVEWATCH III).
First, we need to introduce the algorithm of the SMC grid generation script provided by the Met Office because the grid generation logic is similar. A schematic diagram of the 4-level nearshore refined SMC grid is shown in Fig. 1. The blue grids are the water grids, and the brown grid is the land grid.
The resolution of the terrain data required by SMC grid generation scripts needs to be the same as that of a 1-level grid (the minimum grid size). Then, taking the side length of the base grid (the largest grid) as the step size, the terrain data is looped in the meridional and latitudinal directions, which is equivalent to combining the grid points of the whole terrain to a resolution of 8×8; in this way, each base grid will be judged. If the base grid meets the constraints (the specific constraints will be listed below for easy understanding), the base grid will be included in the SMC grid file. If the base grid does not meet the constraints, the large grid will be evenly divided into four 3-level grids and judged according to the same constraints until the grid can no longer be divided.
The following are the constraints mentioned above. The first two are the constraints that all SMC grid forms must comply with. The third is only for the global offshore refined SMC grids.
(1) The SMC grid can only scale by 1:2 or 1:1.
(2) The depth of the grid must be greater than the minimum depth of the WW3 model.
(3) The grid points close to land must be a 1-level grid.
The constraints of 1 to 3 set a limitation on the grid, that is, a land grid is not allowed within a specific distance (in the following section, we call this distance the restricted radius) of the grid with the exception of the 1-level grid. As shown in Fig. 1, the restricted radius of the 4-level grid is 1+2+4=7. We can also easily derive that the restricted radii of the N-level grids are
In addition, the grid generation process also needs to consider the fusion of grids in the meridional direction with increasing latitude, such as a reduced Gaussian grid. The Met Office uses a 4-layer nested loop structure to implement the above operations, which leads to the refinement level of the SMC grid cannot be changed. Actually, the operational SMC grid of the Met Office is not directly generated by the public program (the operational SMC grid of Met Office is a mixture of global 3-level grid and a few areas of refined 4-level grid) .
The grid generation process itself is a recursive process (the grid is divided continuously until it can no longer be divided). Therefore, we can adopt a recursive loop structure to conduct the grid generation process; in this structure, the level of the SMC grid can naturally be changed by the user.
In the recursive loop, the grid generation process is treated as a function. When a grid does not meet the constraints, the function will call itself until the constraints are met or the grid cannot be divided. The main program flow is shown in Fig. 2, and the recursive part is shown in Fig. 3.
To achieve a flexible grid refinement form, we use a curve to represent the area we need to refine and add hierarchical properties to the curve. In this way, we can refine the grid to the specified level in any area, as shown in Fig. 4.
We only need to modify the last of the three constraints in the nearshore refinement method to apply the constraints to the arbitrary area refinement. We define that the N-level grid is wrapped by the N-level curve and is outside the range of the (N−1)-level curve. If the grid is just crossed by the curve, then that grid is also wrapped by the curve. Correspondingly, the constraints for the arbitrary area refinement are as follows.
(1) The SMC grid can only scale by 1:2 or 1:1.
(2) The depth of the grid must be greater than the minimum depth of the WW3 model.
(3) Except for the base grid, the grids must be within the curve range of the same level, and the grids must be outside the curve range of the lower level.
(4) The base grid must be outside any level of curve and satisfy Constraint 2.
(5) If the curve just passes through a grid, that grid is also considered to be within the range of the curve.
With these new constraints, we can achieve the refinement of an arbitrary area. To meet Constraint 1 (the SMC grid can only scale by 1:2 or 1:1), the following constraints must also be met when using a curve to define the refined area.
(1) No two curves can intersect.
(2) The curves themselves cannot intersect but can be concave.
(3) The lower level curve must be within the range of the higher level curve.
(4) The distance between the N-level curve and the N−1 level curve must be greater than the side length of the N-level grid (the two curves cannot be too close).
The flow chart of the recursive part of the arbitrary area refinement method is shown in Fig. 5.
The ray method is used to judge whether a grid is within the curve; that is, we introduce a ray from the judged grid (for convenience, we define this ray as being parallel to the x-axis and pointing in the positive direction). If the number of intersection points between the ray and the curve is odd, then the judged point is within the curve. If the number of intersections is even, then the judged point is outside the curve (if the ray is tangential to the curve, this is counted as no intersection). The proof of this method is shown below.
As shown in Fig. 6, we draw a ray from Point P, the ray is divided into line segments by the curves, and the spaces on the left and right sides of the curve are always opposite. Since the curve range is limited, we can easily judge that the outermost line segment must be outside the curve. If the number of line segments is even, the line segment where Point P is located is the same space as the outermost line segment (outside the curve). When the number of line segments is odd, Point P is inside the curve.
In the application of the ray method, a polygon is used to approximate the curve. Thus, the number of intersections between the ray and each edge of the polygon needs to be counted. The formula for judging the intersection is shown below.
| $$ \left\{\begin{array}{l}y_{\rm{p}}\geqslant \mathrm{min}\left(y_{\rm{a}},y_{\rm{b}}\right)\\ y_{\rm{p}}\leqslant \mathrm{max}\left(y_{\rm{a}},y_{\rm{b}}\right)\\ x_{\rm{p}} < x_{\rm{i}}\end{array}\right.:{\rm{intersect}}. $$ | (1) |
As shown in Fig. 7, in Eq. (1), p (xp, yp) is the judged point, A (xa, ya) and B (xb, yb) are the endpoints of the edge, and I (xi, yi) is the intersection of the line and ray where segment AB is located.
The curve is continuous and differentiable everywhere; however, a polygon consists of vertices and edges, and therefore, the ray method will be invalid when a ray passes through a vertex of the polygon or coincides with an edge of the polygon, as shown in Fig. 8.
In a given curve, the situations of the red Circles 1, 2, and 3 are the same; there are 0 intersections (the case of tangency is considered as a non-intersections). Red Circle 4 clearly has only one intersection point. To eliminate these misjudgments, the mathematical expression for judging the intersection is adapted to the following equation (the equal sign from the first inequality is removed).
| $$ \left\{\begin{array}{l} y_{\rm{p}} > {\rm{min}}\left({y}_{\rm a},{y}_{\rm b}\right)\\ y_{\rm{p}}\leqslant {\rm{max}}\left({y}_{\rm a},{y}_{\rm b}\right) \\ x_{\rm{p}} < x_{\rm{i}}\end{array}\right.:{\rm{intersect}}. $$ | (2) |
To test the grid generation program, we generate a 9-level nearshore refined grid and a 6-level arbitrary area refined grid.
When generating the 9-level nearshore refined grid (Fig. 9), the number of maximum refined levels in the script is actually 10. Because of spatial limitations, the global grid can only accommodate a 9-level refined grid without changing the terrain resolution. Therefore, the number of grid levels generated will also be limited by space. When generating some local grids, we need to pay attention to this situation. However, even if the maximum refined level does not reach a specific number due to spatial limitations, the generated grid file is not problematic.
Figure 10a shows the polygons used to specify the refined area, and Fig. 10b shows the final generated grid. The arbitrary area refined method supports both convex polygons and concave polygons, and the chosen polygon can pass through land or islands. None of these factors will affect the quality of the final generated grid file.
Finally, a 6-level global SMC grid (Fig. 11a) is generated by using the new algorithm, and numerical experiments are carried out. The experimental results are compared with the 4-level global SMC grid provided by the Met Office (Fig. 11b). The numerical tests of the two grids are based on WAVEWATCH III. Since the ww3 open-access tools on GitHub are still in the developmental stage, they are not included in this paper. A comparison of the grid generation algorithms is shown in Table 1, and their resolutions are shown in Table 2. The grids and some details are shown in Figs 11-13.
| Met Office | Durrant and Saulter | This paper | |
| Refinement method | nearshore refinement | rectangular area refinement | arbitrary area refinement and nearshore refinement |
| Level of refinement | fixed | unfixed | unfixed |
| Degree of completion | completed | under development | completed |
| Algorithm | Region | Resolution |
| 4-level SMC grid | nearshore | lat: 0.058°, lon: 0.087° |
| nearshore | lat: 0.116°, lon: 0.174° | |
| nearshore | lat: 0.232°, lon: 0.348° | |
| open sea | lat: 0.464°, lon: 0.696° | |
| 6-level SMC grid | nearshore (China) | lat: 0.014°, lon: 0.021° |
| nearshore (China) | lat: 0.028°, lon: 0.042° | |
| offshore (China) | lat: 0.058°, lon: 0.087° | |
| Northwest Pacific | lat: 0.116°, lon: 0.174° | |
| North Pacific | lat: 0.232°, lon: 0.348° | |
| global | lat: 0.464°, lon: 0.696° |
The reanalysis data of NCEP’s CFSv2 are used for the wind force, and the spatial resolution of the data is 0.2°. The selected time period is from August 27, 2020, to September 4, 2020 (during which a super typhoon affected the China’s seas). The wind field is preprocessed in SEAWND mode (the wind data are interpolated to each SMC grid point by bilinear interpolation). The wind field scatter diagram obtained after the interpolation is shown in Fig. 14 and Fig. 15, the corresponding wave height is shown in Fig. 16.
In the wave model, the sources of error vary, and the focus here is on the error caused by the use of different SMC grids in wind field interpolations and the impact of this error on the subsequent calculation of the significant wave height. Therefore, only the original wind field and the wind field obtained after the interpolation are compared and analyzed, and the significant wave height is not verified.
The comparison results indicated that due to the high-pass filtering effect of bilinear interpolation, the extreme value of the wind field is reduced, but the reduction is small. The reduction in the 4-level grid is slightly larger than that in the 6-level grid. However, the range of significant wave heights larger than 11 meters calculated by the 4-level grid is larger than that calculated by the 6-level grid, and the extreme value of the significant wave height is also larger north of the typhoon center.
We use the product of the grid area and the square of the wind velocity to characterize the wind energy, as shown in Eqs (3)−(5) below. Moreover, the cumulative energy characterization values of different wind velocities above 10.8 m/s are calculated (to avoid a large relative error, the grids containing the top 16 wind velocities are removed). The cumulative distribution of the characterization of energy at the same time as that shown in Fig. 14 is shown in Fig. 17. Equations (3)−(5) can be expressed as follows:
| $$ {E}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}={S}_{\mathrm{g}\mathrm{i}\mathrm{r}\mathrm{d}}{V}^{2}, $$ | (3) |
| $$ {S}_{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}=\frac{{L}_{\mathrm{l}\mathrm{a}\mathrm{t}}{{L}_{\mathrm{l}\mathrm{o}\mathrm{n}}N}_{\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}\text{-}\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}^{2}{C}^{2}\mathrm{c}\mathrm{o}\mathrm{s}\left(\dfrac{2\text{π} }{360}{L}_{\mathrm{l}\mathrm{a}\mathrm{t}}\right)}{{360}^{2}}, $$ | (4) |
| $$ C=R\times 2\text{π} ,$$ | (5) |
where
The total wind energy of the two grids is slightly less than that of the raw wind field when the wind velocity is above 10.8 m/s and the relative error is less than 5%. The error of the 6-level grid is slightly less than that of the 4-level grid. However, when the statistical wind velocity threshold reaches 30 m/s (near the center of the typhoon), the relative error of the total wind energy of the 4-level grid begins to increase and fluctuates sharply. The total wind energy with velocities greater than 35 m/s even exceeds the raw wind field by approximately 25%. Although the relative error of the wind field energy of the 6-level grid also increases near the center of the typhoon, the relative error is always negative, and the absolute value of the error of the 6-level grid is also significantly smaller than that of the 4-level grid.
The analysis shows that when the grid resolution is larger than or close to the wind resolution, bilinear interpolation will not only lead to high-pass filtering but will also redistribute the energy in different wind speed ranges. The algorithm provided by the Met Office cannot refine the grid of a certain area. Improving the grid resolution of the global open sea will lead to a sharp increase in the total number of grids and reduce the computational efficiency. Durrant and Saulter’s algorithm can improve the resolution of a specific area, but with their method, it is difficult to match a rectangular area with a complex coastline, thus reducing the efficiency of the grid refinement of a coastal area. The algorithm developed in this paper enables users to customize the area and the level of refinement, minimize the number of grids, and improve the resolution of the area of interest.
A new SMC grid generation program has been developed that can not only generate a nearshore refined SMC grid at any level but can also refine the grid in arbitrary areas. Some test grids are generated to test the function of the new algorithm. A numerical test is also conducted. We use the new algorithm to generate a 6-level SMC grid while refining of the North Pacific and offishore(China) regions and compare it with the 4-level nearshore refined SMC grid generated by the Met Office’s algorithm through a typhoon simulation. The contrasting results indicate that an inappropriate grid resolution will affect the accuracy of the bilinear interpolation of the wind field. The new grid generation algorithm provided in this paper can effectively alleviate this problem and improve the flexibility of the SMC grid. The code of the new algorithm in this paper is available on request. Anyone who needs the code can contact the first author directly.
| [1] |
Bunney C, Saulter A. 2015. An ensemble forecast system for prediction of Atlantic–UK wind waves. Ocean Modelling, 96: 103–116. doi: 10.1016/j.ocemod.2015.07.005
|
| [2] |
Casas-Prat M, Wang X L, Swart N. 2018. CMIP5-based global wave climate projections including the entire Arctic Ocean. Ocean Modelling, 123: 66–85. doi: 10.1016/j.ocemod.2017.12.003
|
| [3] |
Chawla A, Tolman H L, Gerald V, et al. 2013. A multigrid wave forecasting model: A new paradigm in operational wave forecasting. Weather and Forecasting, 28(4): 1057–1078. doi: 10.1175/WAF-D-12-00007.1
|
| [4] |
Hsu T W, Ou S H, Liau J M. 2005. Hindcasting nearshore wind waves using a FEM code for SWAN. Coastal Engineering, 52(2): 177–195. doi: 10.1016/j.coastaleng.2004.11.005
|
| [5] |
Li Jianguo. 2008. Upstream nonoscillatory advection schemes. Monthly Weather Review, 136(12): 4709–4729. doi: 10.1175/2008MWR2451.1
|
| [6] |
Li Jianguo. 2011. Global transport on a spherical multiple-cell grid. Monthly Weather Review, 139(5): 1536–1555. doi: 10.1175/2010MWR3196.1
|
| [7] |
Li Jianguo. 2012. Propagation of ocean surface waves on a spherical multiple-cell grid. Journal of Computational Physics, 231(24): 8262–8277. doi: 10.1016/j.jcp.2012.08.007
|
| [8] |
Li Jingkai, Ma Yunrui, Liu Qingxiang, et al. 2019. Growth of wave height with retreating ice cover in the Arctic. Cold Regions Science and Technology, 164: 102790. doi: 10.1016/j.coldregions.2019.102790
|
| [9] |
Li Jianguo, Saulter A. 2014. Unified global and regional wave model on a multi-resolution grid. Ocean Dynamics, 64(11): 1657–1670. doi: 10.1007/s10236-014-0774-x
|
| [10] |
Popinet S, Gorman R M, Rickard G J, et al. 2010. A quadtree-adaptive spectral wave model. Ocean Modelling, 34(1/2): 36–49. doi: 10.1016/j.ocemod.2010.04.003
|
| [11] |
Qi Jianhua, Chen Changsheng, Beardsley R C, et al. 2009. An unstructured-grid finite-volume surface wave model (FVCOM-SWAVE): Implementation, validations and applications. Ocean Modelling, 28(1–3): 153–166. doi: 10.1016/j.ocemod.2009.01.007
|
| [12] |
Rasch P J. 1994. Conservative shape-preserving two-dimensional transport on a spherical reduced grid. Monthly Weather Review, 122(6): 1337–1350. doi: 10.1175/1520-0493(1994)122<1337:CSPTDT>2.0.CO;2
|

| Met Office | Durrant and Saulter | This paper | |
| Refinement method | nearshore refinement | rectangular area refinement | arbitrary area refinement and nearshore refinement |
| Level of refinement | fixed | unfixed | unfixed |
| Degree of completion | completed | under development | completed |
| Algorithm | Region | Resolution |
| 4-level SMC grid | nearshore | lat: 0.058°, lon: 0.087° |
| nearshore | lat: 0.116°, lon: 0.174° | |
| nearshore | lat: 0.232°, lon: 0.348° | |
| open sea | lat: 0.464°, lon: 0.696° | |
| 6-level SMC grid | nearshore (China) | lat: 0.014°, lon: 0.021° |
| nearshore (China) | lat: 0.028°, lon: 0.042° | |
| offshore (China) | lat: 0.058°, lon: 0.087° | |
| Northwest Pacific | lat: 0.116°, lon: 0.174° | |
| North Pacific | lat: 0.232°, lon: 0.348° | |
| global | lat: 0.464°, lon: 0.696° |
| Met Office | Durrant and Saulter | This paper | |
| Refinement method | nearshore refinement | rectangular area refinement | arbitrary area refinement and nearshore refinement |
| Level of refinement | fixed | unfixed | unfixed |
| Degree of completion | completed | under development | completed |
| Algorithm | Region | Resolution |
| 4-level SMC grid | nearshore | lat: 0.058°, lon: 0.087° |
| nearshore | lat: 0.116°, lon: 0.174° | |
| nearshore | lat: 0.232°, lon: 0.348° | |
| open sea | lat: 0.464°, lon: 0.696° | |
| 6-level SMC grid | nearshore (China) | lat: 0.014°, lon: 0.021° |
| nearshore (China) | lat: 0.028°, lon: 0.042° | |
| offshore (China) | lat: 0.058°, lon: 0.087° | |
| Northwest Pacific | lat: 0.116°, lon: 0.174° | |
| North Pacific | lat: 0.232°, lon: 0.348° | |
| global | lat: 0.464°, lon: 0.696° |