| Citation: | WANG Yunhua, LI Qun, ZHANG Yanmin. A statistical distribution of quad-pol X-band sea clutter time series acquired at a grazing angle[J]. Acta Oceanologica Sinica, 2018, 37(3): 94-102. doi: 10.1007/s13131-018-1202-8 |
The Changjiang River (also known as the Yangtze River) diluted water (CDW) has a significant impact on the circulation structure, water mass composition, and sediment deposition in the Yellow Sea (YS) and the East China Sea (ECS). The CDW generally enters the YS and ECS and spreads out in a plume and the surface salinity around the Changjiang River Estuary shows significant seasonal variation (Wu et al., 2020) although observations indicate that isolated low-salinity water lenses (LSWLs) occasionally detach from the main body of the CDW (Pu, 2002). These LSWLs are an important factor causing area eutrophication and hypoxia in the Changjiang River Estuary and its adjacent waters (Xuan et al., 2012); thus, this topic has attracted considerable attention from ecological dynamics scientists (Kim et al., 2009; Li et al., 2002, 2019; Zhang et al., 2019). Studies on the LSWL mechanism have been conducted. By analyzing observed data from the area east of Cheju Island, Lie et al. (2003) suggested that the separation of CDW patches from the shallow shelf area and upwelling favorable southerly winds in summer are the main contributors. Chen et al. (2008) used the unstructured-grid, Finite-Volume Coastal Ocean Model (FVCOM) to simulate a LSWL in the sea west of 123°E and proposed that the detachment of this LSWL is associated with eddies generated by baroclinic instability across the plume front. Using the Regional Ocean Modeling System (ROMS), Moon et al. (2010) simulated a LSWL under ideal wind, tide and runoff conditions and suggested that the strengthening of tidal mixing during the spring tide plays an important role in the detachment of the LSWL. Wu et al. (2011) indicated that strong upwelling during the spring tide can disconnect part of the Changjiang River plume. Xuan et al. (2012) used the MIT general circulation model (MITgcm) to analyze the dynamic mechanism responsible for LSWL detachment and indicated that wind mixing, wind-driven northward currents and wind-induced upwelling are the three driving forces underlying the detachment of the LSWL. Using the POM-
Both winds and tides are generally believed to have important influences on LSWL detachment. In recent years, upwelling water has been found in the detachment region (Moon et al., 2010; Wu et al., 2011; Xuan et al., 2012). Although the magnitude of the upwelling velocity is small, an upwelling can carry saline seawater from the bottom to the surface and therefore can significantly impact the distribution of salinity, which may be conducive to detachment. However, the role of upwelling water on detaching the LSWL has not been thoroughly explored; thus, the effects and dynamic mechanism of upwelling during the evolution of the LSWL need to be further studied. In this paper, the dynamic mechanism of the LSWL observed in August 2006 is studied with a focus on the effects of upwelling on the LSWL.
The observed data were obtained from a cruise survey carried out during July 27 to August 12, 2006. During the cruise, conductivity-temperature-depth (CTD) instruments were used in the field program to measure the vertical profiles of water temperature and salinity. The path of the cruise extended alongshore from 29.8°N to 32.3°N and offshore from 121°E to 128°E. The sea near the Changjiang River Estuary was the key observation area, and the minimum latitudinal resolution was (1/9)°.
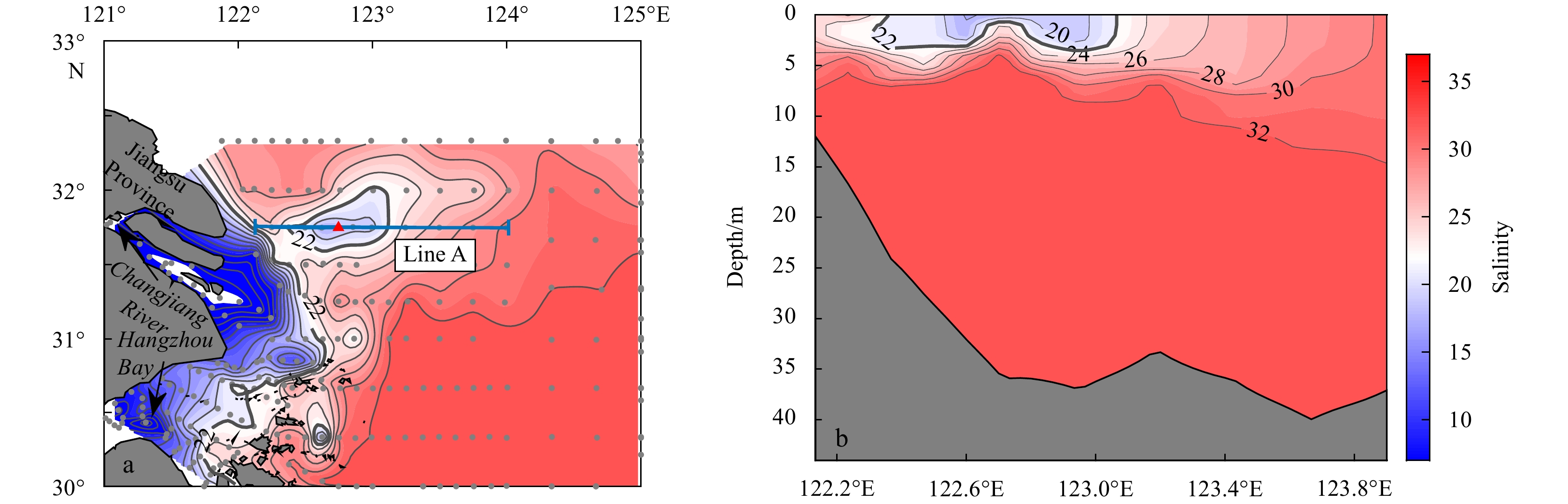
The distribution of surface salinity in the survey area is shown in Fig. 1a. The salinity front (less than 22) near the Changjiang River Estuary extends toward the southeast, thus reflecting the jet pattern of the CDW (Wang et al., 2012), whereas the CDW from the Changjiang River Estuary extends northeastward in a plume pattern. The detachment of the LSWL occurs on the interior side of the river plume at approximately 31.8°N, 122.7°E. The LSWL isolated by the 22 isohaline has an elliptical shape, and the value of the central closed isohaline is 20. The size of the LSWL (the diameter of the long axis of the outermost closed isohaline) is 70 km. Figure 1b shows the vertical salinity distribution along Line A through the center of the LSWL. The upper salinity stratification structure is obvious, and the lower water is mixed uniformly. Additionally, the 32 isohaline obviously descends from west to east. This phenomenon was discussed by Zhao (1993) in consideration of upwelling.
The distribution of surface temperature is depicted in Fig. 2a. There is a clear, cold water belt between 122°E and 123°E that has two cold centers. The first cold center is located at the junction of the Changjiang River Estuary and Hangzhou Bay, while the second cold center is located northeast of the Changjiang River Estuary on the west side of the LSWL. Low surface temperature reveals the spread of cold water and thus the range of upwelling (Li et al., 2018). Figure 2b shows the vertical temperature distribution along Line A, and it consists of an upper mixed layer, a thermocline layer, and a lower mixed layer. The thicknesses of the upper mixed layer and the thermocline layer are both 5–10 m, and the isotherm below the thermocline gradually rises from east to west. Similar to the 32 isohaline, the 25°C isotherm rises from east to west. Both the isotherms and the isohalines suggest that cold and saline deep water upwells along the bottom slope.
The POM
| $${\sigma _1} = \frac{{z - \eta }}{{H + \eta }} = \frac{{z - \eta }}{D},$$ | (1) |
where
| $$\left\{ \begin{aligned} & {\sigma _2} = \frac{{z - \eta }}{{H + \eta }}{\rm{ = }}\frac{{z - \eta }}{{{D_1}}}\;\;\;\;\;\;\;\;\;{\rm{ }}H \leqslant {H_0} \\ & {\sigma _2} = \frac{{z - \eta }}{{{H_0} + \eta }} = \frac{{z - \eta }}{{{D_1}}}\;\;\;\;\;\;{\rm{ }}H > {H_0} \end{aligned} \right..$$ | (2) |
In contrast, the
The Eulerian-Lagrangian method (ELM) is used to address the effect of the current on salinity. The salinity equation used in the ELM in
| $$\frac{{{\rm{d}}S}}{{{\rm{d}}t}} = F,$$ | (3) |
where
| $$\left\{ {\begin{aligned} & {F = \frac{1}{{D_1^2}}\frac{\partial }{{\partial \sigma }}\left({K_H}\frac{{\partial S}}{{\partial \sigma }}\right) + {F_S}}\quad{z \geqslant - {H_0}}\\ & {F = \frac{\partial }{{\partial z}}\left({K_H}\frac{{\partial S}}{{\partial z}}\right) + {F_S}}\qquad\;\;{z < - {H_0}} \end{aligned}} \right.,$$ | (4) |
where
| $${S^{n + 1}}(Q) = {S^n}(P) + F\Delta t.$$ | (5) |
The change of salinity at point
The method of determining the location of point
| $$\left\{ \begin{aligned} & x(P) = x(Q) - {u^{n + 1}}(Q) \Delta t \\ &y(P) = y(Q) - {v^{n + 1}}(Q) \Delta t \\ &\sigma (P) = \sigma (Q) - {\omega ^{n + 1}}(Q) \Delta t \end{aligned} \right.,$$ | (6) |
where
The computational domain covers the Bohai Sea, the YS and the ECS (Fig. 4a). The numerical grids are shown in Fig. 4b. The minimum and maximum distances between the grids are 1 540 m and 25 000 m, respectively. In the vertical direction, the current calculation uses 20 vertical
For convenience, the numerical simulation of the LSWL in summer 2006 is called CASE06, which couples the tidal currents and circulation in consideration of runoff, winds, tides (the M2, S2, K1 and O1 tidal constituents), the Taiwan Warm Current (TWC), the Kuroshio, the Tsushima Warm Current, and the baroclinic effect. The Changjiang River discharge is obtained from the monthly averaged flux at the Datong hydrometric station, which is ~640 km upstream from the river mouth. The wind force is obtained from 6-hourly NCEP/NCAR reanalyzed wind data. The climatological averages of the salinity and sea temperature in summer are used as the original field data, and the sea temperature does not change with time in the calculation. The calculation coupled the tidal current and the circulation begins on July 2, 2006, and runs simultaneous with the salinity calculation on July 9, 2006. The numerical scheme of CASE06 is similar to that of a previous study (Zhang et al., 2011), which introduced more details of the model and its validation.
Figure 5 shows part of the simulated surface salinity. Beginning on August 3, low-salinity water (less than 30) extended northeastward from the Changjiang River mouth in a tongue shape. At 2:00 on August 7, the LSWL detached from the interior side of the river plume at approximately 32°N, 122.9°E and then gradually moved northeastward. After August 10, the central position of the LSWL was nearly fixed. Finally, the LSWL disappeared at 15:00 on August 19. During August 7 to 19, the value of the central closed isohaline increased from 18 to 28 and the size of the LSWL was generally 20–85 km. The LSWL disappeared briefly several times but consistently maintained a tongue shape.
Compared with the observed characteristics, the real-case simulation of the detachment of the LSWL in August 2006 shows that the shape of the LSWL remained basically the same. Numerical experiments to further reveal the mechanism of detachment are therefore justifiable.
In this section, seven experiments (Table 1) are designed to examine the influences of winds, tides, vertical mixing, and upwelling and the baroclinic effect on the LSWL. We take CASE06 as the control test. Based on CASE06, the arrangement of CASE06a removes the wind forcing to eliminate its influence. CASE06b uses the same model settings as CASE06, although the wind is changed to a steady southerly wind of 4 m/s. For CASE06c and CASE06d, the effects of tides and vertical mixing are removed, respectively, while all other physical processes remain intact. The vertical velocity in the
| Case | Wind | Tide | Vertical mixing | Vertical velocity | Baroclinity |
| CASE06 | Y | Y | Y | Y | Y |
| CASE06a | N | Y | Y | Y | Y |
| CASE06b | Y2) | Y | Y | Y | Y |
| CASE06c | Y | N | Y | Y | Y |
| CASE06d | Y | Y | N | Y | Y |
| CASE06e | Y | Y | Y | N | Y |
| CASE06f | Y | Y | Y | Y | N |
| CASE06g | Y | Y | Y | Y | Y3) |
| Note: 1) Y means that the dynamic factors are considered in the simulation, and N means that dynamic factors are excluded from the simulation. 2) The wind is changed to a steady southerly wind of 4 m/s. 3) The BPG is calculated by the climatological average of the salinity and sea temperature. | |||||
Figure 6 shows the NCEP 5-day average wind from August 2 to 21, 2006. Given that LSWL detachments occur within the 0–10 m layer and wind plays an important role in currents, the vertical average of the currents in the 0–10 m layer is used to analyze the current during the detachment process (Xuan et al., 2012). Based on the simulated results of CASE06, the Eulerian residual current (ERC) is calculated. Figure 7 shows the 5-day average ERC in the 0–10 m layer. During August 2 to 6, the CDW expansion area was controlled by a southeasterly wind with a mean speed of 4.0–5.5 m/s (Fig. 6a). The ERC between 31°N and 33°N had an average speed of 10 cm/s and was divided into two parts by the 30 m isobath: a western part, in which the ERC was oriented mainly toward the north, and an eastern part, in which the ERC was oriented mainly toward the northeast (Fig. 7a). During August 7 to 11, the sea surface was controlled by a southeasterly wind with a mean speed of 3.5–6.0 m/s (Fig. 6b). The horizontal current structure was similar to that during the last phase (August 2 to 6), although the velocity was slightly weakened (Fig. 7b). During August 12 to 16, the southeasterly wind weakened and its average speed was less than 1 m/s (Fig. 6c), which weakened the ERC significantly (Fig. 7c). During August 17 to 21, a northerly wind prevailed with an average speed of 4.0–6.0 m/s (Fig. 6d). The ERC flow mainly toward the southwest at a speed of approximately 13 cm/s (Fig. 7d).

The evolutionary characteristics of the wind, ERC and LSWL revealed a close relationship. During August 2 to 11, forced by the sustained southeasterly wind, the ERC vectors showed differences on both sides of the 30 m isobath, with a northward current on the left side and a current mainly to the northeast on the right side. The nonuniform ERC imposed an uneven northward force on the CDW and cut it off, which facilitated LSWL detachment (Xuan et al., 2012; Zhang et al., 2014b). During August 12 to 16, the light southeasterly wind weakened the ERC, which stabilized the LSWL. During August 17 to 21, the strong northerly wind caused the ERC to flow southward; and under the effect of this current, the CDW receded to the south, which caused the LSWL to disappear.
Two numerical simulations, CASE06a and CASE06b, were conducted to test the effects of winds on the LSWL. The easterly and northeasterly offshore expansions of the CDW in CASE06a were weaker than those in CASE06 and there was no LSWL (not shown). However, two detachment events appeared in CASE06b: the first detachment occurred on the interior side of the river plume and lasted from 05:00 on August 7 to 14:00 on August 9 (Fig. 8), while the second detachment occurred at the same location as the first detachment but lasted from 03:00 on August 22 to 03:00 on August 23.
These two numerical simulations considered either no wind or only a light southerly wind. In comparison with CASE06, the simulation results showed either no detachment or a detachment region relatively close to the Changjiang River Estuary. These results indicated that the southerly wind had an important impact on the detachment and offshore movement of the LSWL.
The tidal data in this section are taken from the tide table produced by the United Kingdom (UK) Hydrographic Office. Figure 9 shows the tide level at Lühuashan station (30.82°N, 122.6°E) in August 2006. Neap tides occurred on August 3 and 18, whereas spring tides occurred on August 10 and 25. The LSWL detached on August 7, which was the time of the transition from neap tide to spring tide.
To verify the role of tides in detachment, CASE06c was conducted. The results show that no LSWL was detached in CASE06c (not shown), confirming that tides were necessary for the formation of LSWL. Zhang et al. (2014a, b) analyzed the evolution of the vertical salinity structure in the detachment region from neap tide to spring tide and suggested clear vertical salinity stratification during the neap tide period; further, these authors indicated that the tide-induced vertical mixing gradually strengthened from neap tide to spring tide and that the surface salinity in the shallow water increased faster than that in the deep water, which was helpful for forming the LSWL. In Fig. 10, we examine the vertical salinity structure along Line B (marked in Fig. 5b) in CASE06. The variation in the salinity distribution from neap tide (August 3) to spring tide (August 10) was consistent with the numerical simulation results of Zhang et al. (2014a, b). The results demonstrate that tidal mixing may be attributed to detachment.
To examine the role of tidal mixing in the detachment discussed above, we tried to eliminate tidal mixing. In CASE06d, the coefficients of the vertical eddy diffusivity (Kh) are set to 0, while all other settings are consistent with those in CASE06. Compared with Fig. 5, the spatial pattern of CDW patches in CASE06d exhibits major alterations. The low-salinity water quickly extended farther northeastward and clearly detached from the interior side of the river plume at approximately 32.2°N, 122.2°E (Fig. 11a). These results reflect that tidal mixing played a limited role in detaching the LSWL.
Figure 7 also shows the 5-day average vertical velocity in the 0–10 m layer from August 2 to 21, 2006 in CASE06. During August 2 to 6, the upwelling was distributed mainly along the coastline of Jiangsu and near the Changjiang River Estuary, and the maximum upwelling velocity was approximately 0.3×10–4 m/s. During August 7 to 11, upwelling occurred along the 30 m isobath at a mean speed of 0.10×10–4–0.27×10–4 m/s. During August 12 to 16, the upwelling along the 30 m isobath was slightly weakened, and after August 16, nearby upwelling disappeared from the study area.
Figure 12 shows the effects of upwelling on the detachment along Line C during August 7 to 11 in CASE06. Significant upwelling occurred in the region with a water depth of approximately 30 m, and the maximum velocity was approximately 0.3×10–4 m/s. The 28 isohaline, which is located at a depth of 30 m, was uplifted by upwelling, which brought high-salinity water to the surface layer and disconnected part of the Changjiang River plume. This upwelling event can be validated with previous observations. Hu and Zhao (2008) used remote sensing data to investigate upwelling events in the coastal area of Zhejiang and found that upwelling is generally located around the 30 m isobath, which is similar to the results of this paper.

The evolutionary characteristics of these upwelling phenomena and the LSWL were closely related. The strong upwelling along the coast brought high-salinity water from the deeper layer to the surface layer during August 2 to 6. This upwelling served to cut off the CDW vertically. Under the influence of strong upwelling in the detachment region, an isolated LSWL quickly appeared. During August 7 to 11, the LSWL moved northeastward, with a new upwelling area appearing along the 30 m isobath. The upwelling weakened slightly from August 12 to 16 but nevertheless cut off the CDW continuously, thereby stabilizing the LSWL.
If
| $${w_z} = D\omega + (1 + \sigma)\frac{{\partial \zeta }}{{\partial t}} + u\left({\frac{{\partial \zeta }}{{\partial x}} + \sigma \frac{{\partial D}}{{\partial x}}} \right) + v\left({\frac{{\partial \zeta }}{{\partial y}} + \sigma \frac{{\partial D}}{{\partial y}}} \right).$$ | (7) |
The numerical simulation CASE06e was conducted to quantify the effects of upwelling on the detachment of the LSWL. In CASE06e,
| $${\omega _s} = - \frac{{1 + \sigma }}{D}\frac{{\partial \zeta }}{{\partial t}} - \frac{u}{D}\left({\frac{{\partial \zeta }}{{\partial x}} + \sigma \frac{{\partial D}}{{\partial x}}} \right) - \frac{v}{D}\left({\frac{{\partial \zeta }}{{\partial y}} + \sigma \frac{{\partial D}}{{\partial y}}} \right).$$ | (8) |
When using Eq. (5) to calculate salinity, the particle location of point
No detachments formed during the entire simulation of CASE06e. Figure 11b shows the simulated surface salinity at 01:00 on August 12 in CASE06e. Compared with the results depicted in Fig. 5c, the results of CASE06e deviate considerably. The expansion area shrank remarkably and the main body of the CDW was closer to the coast. The outer boundary of the CDW is always defined by a salinity of 31 (Gong et al., 1996; Zhao, 1993). The two simulations differed in the expansion range. The 31 isohaline in CASE06 extended eastward to 124.8°E, while this isohaline extended to only 123.8°E in CASE06e. Although the CDW in CASE06e still tended to expand northeastward, due to the lack of the vertical cutting force of upwelling, it was impossible to isolate the LSWL.
Two numerical simulations, CASE06f and CASE06g, were conducted to test the baroclinic effect on the LSWL. In CASE06f, the influence of the baroclinic effect was not considered at all; similarly, in CASE06g, the baroclinic feedback effect caused by changing salinity was not considered.
Figure 13a shows part of the simulated surface salinity for CASE06f. Beginning on August 1, the CDW expanded with a pattern resembling a narrow tongue toward the northeast. At 15:00 on August 12, the LSWL detached from the interior side of the river plume at approximately 32.6°N, 122.9°E and disappeared at 20:00 on August 13. The value of the outermost closed isohaline was 25, and the size of this LSWL was 65 km.
Figure 13b shows part of the simulated surface salinity for CASE06g. Beginning on August 3, the CDW spread from south to north. At 05:00 on August 6, the LSWL detached from the interior side of the river plume at approximately 32°N, 122.2°E and then gradually moved northeastward. Finally, the LSWL disappeared at 06:00 on August 12. From August 6 to 12, the LSWL disappeared briefly several times, the CDW maintained a tongue pattern, and the value of the central closed isohaline of the LSWL increased from 14 to 25. The size of the LSWL was generally 27–40 km.
In comparison with that shown in Fig. 5a, the CDW of CASE06f expanded northeastward in a narrower tongue pattern. Additionally, the LSWL lasted for a shorter time than that in CASE06. The baroclinic feedback effect was not considered in CASE06g, and the expansion pattern of the CDW changed little, while the LSWL lasted for a slightly shorter time.
According to previous studies, the formation mechanisms responsible for upwelling are diverse. Lü et al. (2006) suggested that tidal mixing plays a dominant role in inducing upwelling. Additionally, topography exerts profound influences on upwelling. Zhu (2003) studied the upwelling off the Changjiang River Estuary by conducting numerical tests and proposed that in the northern submarine valley the baroclinic effect primarily accounts for upwelling. Zhao et al. (2003) found that the upwelling off the Changjiang River Estuary was induced by the interaction between the TWC and the slope bottom topography and that the southerly wind had an important impact on the upwelling in the upper layer. Ni et al. (2014) suggested that the Coriolis force and pressure gradient force were the main forcing factors for the upwelling off the Changjiang River Estuary.
As previously discussed, four experiments (Table 2) were designed to examine the influences of the baroclinic effect, wind forcing, and tides on upwelling during the evolution of the LSWL. The CASE06h experiment was designed to analyze the influences of the baroclinic effect on the upwelling, and the same model settings for CASE06 were used for CASE06h except that the salinity of this experiment was fixed and the BPG was set to 0. To analyze the influences of the wind forcing and tides on upwelling and to avoid the indirect effects of salinity changes, the arrangements of CASE06i and CASE06j, which were based on CASE06h, eliminated the wind forcing and tide components, respectively. For CASE06k, the effects of all dynamic factors except tides were removed. These four experiments were used to simulate the currents during August 2 to 21.
| Case | Baroclinity | Wind | Tide | River discharge and open boundary current |
| CASE06h | N2) | Y | Y | Y |
| CASE06i | N2) | N | Y | Y |
| CASE06j | N2) | Y | N | Y |
| CASE06k | N2) | N | Y | N |
| Note: 1) Y means that the dynamic factors were considered in the simulation, and N means that the dynamic factors were excluded from the simulation. 2) The salinity of this experiment was fixed and the BPG was set to 0. | ||||
The simulation results showed that the upwelling distribution of CASE06h (Fig. 14) during August 7 to 11 was different from that of CASE06 (Fig. 7b), although these differences were not obvious in some areas. The intensity of upwelling in the sea north of 32°N slightly increased, and the upwelling patterns exhibited few alterations. The upwelling patterns south of 32°N showed more obvious changes than those in the north. Moreover, the upwelling area near the Changjiang River Estuary moved offshore with a slightly decreased intensity in CASE06h and a new upwelling area appeared near the Zhoushan Islands. The upwelling distributions in the other periods of August 2 to 21 did not change much compared with those in CASE06.
Wind-driven upwelling is a classic conceptual model for upwelling on inner shelves. In coastal seas, the steady blowing of winds that promote for upwelling drives the surface water to move offshore within the surface Ekman layer. Divergence along the coast is created, and deeper water must move onshore and toward the surface to maintain mass conservation.
Compared with the results in Fig. 6a, CASE06i shows a large vertical change from August 2 to 6 (not shown). The upwelling area along the Jiangsu coast and near the Zhoushan Islands nearly disappeared. During August 7 to 21, the general upwelling patterns in the CASE06i exhibited few alterations: during August 7 to 16, there were two strong upwelling areas in the northeast sea off the Changjiang River Estuary and along the 30 m isobath in both CASE06h and CASE06i, while the upwelling was weak during August 17 to 21. The differences between CASE06h and CASE06i suggest that the upwelling along the Jiangsu coast during August 2 to 6 was induced by the persistent southeasterly wind. However, winds played a limited role in inducing upwelling during August 7 to 16.
Lü et al. (2007) used the Marine Science and Numerical Modeling (MASNUM) wave-tide-circulation coupled numerical model to simulate the upwelling patterns off the Changjiang Estuary and in the adjacent waters off the Zhejiang coast, and the results suggested that tidal mixing plays a dominant role in inducing upwelling. To analyze the tidal influences on upwelling and avoid the indirect effects of salinity changes on upwelling, CASE06j was designed based on CASE06h but with the elimination of tides.
Compared with those of CASE06h, the upwelling areas of CASE06j from August 2 to 6 exhibited few alterations. However, from August 7 to 16, the upwelling areas along the 30 m isobath disappeared (not shown). The differences between CASE06h and CASE06j indicate that the upwelling during August 7 to 16 was induced by tides.
Comparing the evolution of the upwelling (Fig. 7) with the tide level at Lühuashan station (Fig. 9), we find a significant upwelling response to the spring-neap tide modulation along the 30 m isobath. During the neap tide period (August 2 to 6), the upwelling along the 30 m isobath was weak. Subsequently, as the spring tide arrived (August 7 to 11), the tidal forcing was gradually strengthened, which induced strong upwelling along the 30 m isobath. As the tidal forcing weakened during the transition time from spring tide to neap tide (August 12 to 16), the upwelling became weaker than that in the last phase. Finally, upwelling disappeared during the neap tide period (August 17 to 21).
To further verify the effects of tides on the upwelling, the upwelling on August 3, 7, and 10 was simulated by CASE06i according to the tide level at Lühuashan station. The simulated results are shown in Fig. 15. For the study region, only very weak upwelling was present at neap tide (August 3). The upwelling along the 30 m isobath gradually appeared; finally, the vertical velocity reached its maximum at spring tide (August 10). These simulation results confirm that the upwelling along the 30 m isobath was induced predominantly by tides.
To determine the dynamics of the upwelling under the interactions of tides and topography, CASE06k was employed to simulate the ERC at spring tide (August 10). Figure 16 shows the distribution of the bottom ERC (
By combining observed temperature and salinity data, we found an isolated LSWL offshore from the Changjiang River Estuary in August 2006. The LSWL isolated by the 22 isohaline had an elliptical shape, and the value of the center closed isohaline was 20 psu. The vertical structures of the salinity and temperature along Line A indicated that cold and saline deep water upwells along the bottom slope.
In this study, the POM
Winds played important roles in the formation and evolution of the LSWL. During August 2 to 6, the persistent southeasterly wind induced the northwestward expansion of the LSWL. ERC vectors, which imposed an uneven northward force on the CDW, showed differences between the nearshore and far-shore detachment regions. Strong upwelling occurred along the Jiangsu coast and off the Changjiang River Estuary, and it carried high-salinity water to the surface layer and strengthened vertical mixing, which was favorable for the detachment of the LSWL. During August 7 to 11, with the continued easterly wind, the northeastward ERC in the detachment region was conducive to driving the LSWL offshore. A new upwelling area appeared along the 30 m isobath, which stabilized the LSWL. During August 12 to 16, the light wind in the study region weakened the ERC and the upwelling; hence, the LSWL remained steady. After August 17, the upwelling disappeared and the strong southwestward ERC induced by the strong northerly wind drove the LSWL onshore, which caused the LSWL area to decrease gradually until it disappeared.
Numerical experiments showed that tides are a necessary condition for the formation of LSWLs. Zhang et al. (2014a, b) indicated that tide-induced vertical mixing gradually strengthens from neap tide to spring tide, which is helpful for forming a LSWL. However, an interesting phenomenon presented herein is that the LSWL did not disappear when vertical mixing ceased. These results indicated that the tide affects detachment by physical processes other than tidal mixing.
Upwelling is crucial in detachment events. Furthermore, the influences of three dynamic mechanisms on upwelling, namely, the baroclinic effect, wind forcing and tides, were also discussed. The baroclinic effect played only a limited role in the upwelling along the Jiangsu coast and in the northeast sea off the Changjiang River Estuary. The persistent southeasterly wind during August 2 to 6 induced strong upwelling near the Changjiang River Estuary and along the Jiangsu coast; however, the direction and intensity of the wind during August 7 to 21 were not conducive to inducing upwelling. Tide-induced upwelling gradually increased during the transition from neap tide to spring tide. The bottom ERC near the coastal area with depths shallower than 30 m flowed offshore, and in the sea area north of 32°N, the bottom ERC flowed onshore across the 30 m isobath at spring tide. The tidal residual currents converged at the 30 m isobath, and the bottom topography provided an inclined plane that the bottom ERC could climb.
The distribution of nutrients and dissolved oxygen is greatly affected by LSWLs. In particular, detachment will change the local ecological environment. Our work can therefore provide theoretical suggestions for the protection of ecological environments and aquaculture in the Changjiang River Estuary. However, there are still many unclear aspects; for example, the TWC and Changjiang River discharge may affect the upwelling near the Changjiang River mouth. Therefore, more numerical simulations are needed for further study.
|
Brusch S, Lehner S, Fritz T, et al. 2011. Ship surveillance with TerraSAR-X. IEEE Transactions on Geoscience and Remote Sensing, 49(3): 1092-1103
|
|
Chapman R D, Gotwols B L, Sterner R E. 1994. On the statistics of the phase of microwave backscatter from the ocean surface. Journal of Geophysical Research, 99(C8): 16293-16301
|
|
Conte E, De Maio A, Galdi C. 2004. Statistical analysis of real clutter at different range resolutions. IEEE Transactions on Aerospace and Electronic Systems, 40(3): 903-918
|
|
Conte E, Longo M, Lops M. 1991. Modelling and simulation of non-Rayleigh radar clutter. IEE Proceedings F-Radar and Signal Processing, 138(2): 121-130
|
|
Cui Limin, He Yijun, Shen Hui, et al. 2010. Measurements of ocean wave and current field using dual polarized X-band radar. Chinese Journal of Oceanology and Limnology, 28(5): 1021-1028
|
|
Farina A, Gini F, Greco M V, et al. 1997. High resolution sea clutter data: statistical analysis of recorded live data. IEE Proceedings-Radar, Sonar and Navigation, 144(3): 121-130
|
|
Farina A, Russo A, Studer F A. 1986. Coherent radar detection in log-normal clutter. IEE Proceedings F-Communications, Radar and Signal Processing, 133(1): 39-53
|
|
Goodman N R. 1963. Statistical analysis based on a certain multivariate complex Gaussian distribution (an introduction). The Annals of Mathematical Statistics, 34(1): 152-177
|
|
Goodman J W. 1985. Statistical Optics. New York: John Wiley & Sons
|
|
Gradshteyn I S, Ryzhik I M. 2007. Table of Integrals, Series, and Products. 7th ed. London: Academic
|
|
Greco M, Bordoni F, Gini F. 2004. X-band sea-clutter nonstationarity: influence of long waves. IEEE Journal of Oceanic Engineering, 29(2): 269-283
|
|
Hwang P A, Sletten M A, Toporkov J V. 2008. Breaking wave contribution to low grazing angle radar backscatter from the ocean surface. Journal of Geophysical Research, 113(C9): C09017
|
|
Johnson J T, Burkholder R J, Toporkov J V, et al. 2009. A numerical study of the retrieval of sea surface height profiles from low grazing angle radar data. IEEE Transactions on Geoscience and Remote Sensing, 47(6): 1641-1650
|
|
Kuttikkad S, Chellappa R. 1994. Non-Gaussian CFAR techniques for target detection in high resolution SAR images. In: IEEE International Conference in Image Processing. Vol. 1. Austin, TX: IEEE, 910-914
|
|
Lee P H Y, Barter J D, Beach K L, et al. 1995. X-band microwave backscattering from ocean waves. Journal of Geophysical Research, 100(C2): 2591-2611
|
|
Lee J S, Hoppel K W, Mango S A, et al. 1994a. Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Transactions on Geoscience and Remote Sensing, 32(5): 1017-1028
|
|
Lee J S, Miller A R, Hoppel K W. 1994b. Statistics of phase difference and product magnitude of multi-look processed Gaussian signals. Waves in Random Media, 4(3): 307-319
|
|
Posner F L. 2002. Spiky sea clutter at high range resolutions and very low grazing angles. IEEE Transactions on Aerospace and Electronic Systems, 38(1): 58-73
|
|
Vachon P W, Campbell J W M, Bjerkelund C A, et al. 1997. Ship detection by the RADARSAT SAR: validation of detection model predictions. Canadian Journal of Remote Sensing, 23(1): 48-59
|
|
Wang Yunhua, Li Huimin, Zhang Yanmin, et al. 2015. The measurement of sea surface profile with X-band coherent marine radar. Acta Oceanologica Sinica, 34(9): 65-70
|
|
Yang Y, Xiao S P, Wang X S, et al. 2017. Statistical distribution of polarization ratio for radar sea clutter. Radio Science, 52(8): 981-987,, doi: 10.1002/2017RS006371
|
|
Zhu Hong, Wang Qingping, Tai Ning, et al. 2017. Statistical analysis of high-resolution coherent monopulse radar sea clutter. International Journal of Antennas and Propagation, 2017: 7471918
|
| 1. | Yue Gao, Yi Zhang, Lili Lei, et al. Multi-scale characteristics of an extreme rain event in Shandong Province, produced by Typhoon Lekima (2019). Frontiers in Earth Science, 2023, 10 doi:10.3389/feart.2022.1093545 | |
| 2. | Shanshan Tao, Yunfei Hua, Sheng Dong. Hazard risk assessment of tropical cyclones based on joint probability theory. Acta Oceanologica Sinica, 2023, 42(6): 89. doi:10.1007/s13131-022-2143-9 | |
| 3. | Chengcheng Wan, Yafei Yan, Liucheng Shen, et al. Damage analysis of retired typhoons in mainland China from 2009 to 2019. Natural Hazards, 2023, 116(3): 3225. doi:10.1007/s11069-022-05804-y | |
| 4. | Wei Tang, Yunsi Liu, Qiuyan Li, et al. The Impact of Extreme Weather Events on Bacterial Communities and Opportunistic Pathogens in a Drinking Water Treatment Plant. Water, 2021, 14(1): 54. doi:10.3390/w14010054 | |
| 5. | Fang Chen, Huicong Jia, Enyu Du, et al. Spatiotemporal Variations and Risk Analysis of Chinese Typhoon Disasters. Sustainability, 2021, 13(4): 2278. doi:10.3390/su13042278 | |
| 6. | Xiaojing Xu, Yu Peng, Wen Chen, et al. China Satellite Navigation Conference (CSNC 2021) Proceedings. Lecture Notes in Electrical Engineering, doi:10.1007/978-981-16-3138-2_4 |
| Case | Wind | Tide | Vertical mixing | Vertical velocity | Baroclinity |
| CASE06 | Y | Y | Y | Y | Y |
| CASE06a | N | Y | Y | Y | Y |
| CASE06b | Y2) | Y | Y | Y | Y |
| CASE06c | Y | N | Y | Y | Y |
| CASE06d | Y | Y | N | Y | Y |
| CASE06e | Y | Y | Y | N | Y |
| CASE06f | Y | Y | Y | Y | N |
| CASE06g | Y | Y | Y | Y | Y3) |
| Note: 1) Y means that the dynamic factors are considered in the simulation, and N means that dynamic factors are excluded from the simulation. 2) The wind is changed to a steady southerly wind of 4 m/s. 3) The BPG is calculated by the climatological average of the salinity and sea temperature. | |||||
| Case | Baroclinity | Wind | Tide | River discharge and open boundary current |
| CASE06h | N2) | Y | Y | Y |
| CASE06i | N2) | N | Y | Y |
| CASE06j | N2) | Y | N | Y |
| CASE06k | N2) | N | Y | N |
| Note: 1) Y means that the dynamic factors were considered in the simulation, and N means that the dynamic factors were excluded from the simulation. 2) The salinity of this experiment was fixed and the BPG was set to 0. | ||||
| Case | Wind | Tide | Vertical mixing | Vertical velocity | Baroclinity |
| CASE06 | Y | Y | Y | Y | Y |
| CASE06a | N | Y | Y | Y | Y |
| CASE06b | Y2) | Y | Y | Y | Y |
| CASE06c | Y | N | Y | Y | Y |
| CASE06d | Y | Y | N | Y | Y |
| CASE06e | Y | Y | Y | N | Y |
| CASE06f | Y | Y | Y | Y | N |
| CASE06g | Y | Y | Y | Y | Y3) |
| Note: 1) Y means that the dynamic factors are considered in the simulation, and N means that dynamic factors are excluded from the simulation. 2) The wind is changed to a steady southerly wind of 4 m/s. 3) The BPG is calculated by the climatological average of the salinity and sea temperature. | |||||
| Case | Baroclinity | Wind | Tide | River discharge and open boundary current |
| CASE06h | N2) | Y | Y | Y |
| CASE06i | N2) | N | Y | Y |
| CASE06j | N2) | Y | N | Y |
| CASE06k | N2) | N | Y | N |
| Note: 1) Y means that the dynamic factors were considered in the simulation, and N means that the dynamic factors were excluded from the simulation. 2) The salinity of this experiment was fixed and the BPG was set to 0. | ||||