-
Abstract: Nonlinear internal waves (NLIWs) exhibit robust dynamic submesoscale motions, connecting large-scale tides to small-scale shear instabilities in the ocean. Previous studies have mainly focused on their generation mechanisms and evolution along their paths. Considering their global distribution resulting from the primary origin in tide-topography interaction, there is an increasing cross-disciplinary interest in understanding how these energetic and ubiquitous NLIWs contribute to sediment redistribution in the ocean. This paper presents fundamental theories on NLIWs and comprehensively reviews triggering mechanisms, different types of instability, and sediment responses by summarizing recent theoretical parameterizations, numerical simulations, laboratory experiments, and in-situ observations. We specifically focus on elucidating various types of instability along with their impact on sediment dynamic processes. Finally, we outline several unresolved issues that require further exploration for a quantitative investigation into NLIW-induced sediment transfer in the ocean.
-
1. Introduction
Nonlinear internal waves (NLIWs) are a distinct form of internal waves that predominantly originate from tide-topography interactions, and they have been extensively observed in coastal oceans, lakes, and estuaries worldwide (e.g., Jackson, 2007; Ramp et al., 2004; Jackson et al., 2012; Alford et al., 2015; Chang et al., 2021a, b). NLIWs exhibit a soliton waveform, maintaining its original form over long distances of propagation (Jackson et al., 2012). These waves typically possess high energy with amplitudes reaching up to 240 m and horizontal current speed up to 2.5 m/s (Huang et al., 2016). Consequently, NLIWs can transfer significant amounts of energy density exceeding 5 kJ/m3 as well as an impressive energy flux of approximately 4.5 GW along their elongated crests (Klymak et al., 2006). These dynamic NLIWs can promote the develop of coral reef (Hung et al., 2021) and phytoplankton communities (Villamaña et al., 2017) by diffusing nutrients, affect seafloor geological environment by inducing sediment transfer (Tian et al., 2021), and exert catastrophic impact on marine engineering facilities.
The frequent occurrence and energetic nature of NLIWs have been attributed to various interactions between different types of tides and complicate topography. Five primary generation mechanisms have previously summarized by Jackson et al. (2012): (1) Lee wave generation occurs when an initial disturbance which is mainly driven by tides propagates to submarine sills or banks (Maxworthy, 1979); (2) internal tide evolution takes place as the initial sinusoidal internal tides steepen and disseminate into NLIWs (Li and Farmer, 2011); (3) tidal beam generation happens when tidal beams induce moderate displacements of pycnocline, subsequently evolving into NLIWs (New, 1988); (4) resonant generation occurs when stratified flows are perturbed by a lateral horizontal topographic contraction, resulting critical flows and generation of NLIWs (da Silva and Helfrich, 2008); (5) plume generation occurs when different water masses give birth to pycnocline displacement that evolves into NLIWs (Nash and Moum, 2005). Among these mechanisms, internal tide plays a critical role in generating NLIWs. Compared with other mechanisms that require specific topography and water masses, NLIWs generated by internal tide tends to be more intense, periodicity-regulated, and widely-distributed.
The South China Sea (SCS) is a representative region where large-amplitude NLIWs have been widely observed (Fig. 1). In the SCS, the double-ridge topographic system in the Luzon strait (Zheng et al., 2024) give birth to strong internal tides when barotropic tides pass by. These internal tides steepen nonlinearly as it propagates northwestwards until they break and generate NLIWs near-daily (e.g., Ramp et al., 2004; Zhao et al., 2004). Recent long-term measurements in the SCS show comprehensive temporal variabilities of NLIWs from hourly to interannual timescales (Huang et al., 2022b). These variabilities are regulated by variations in mesoscale dynamic processes and tides. Moreover, the associated shear instability within these NLIWs exhibit seasonal variability due to the notable impacts of near-inertial waves and mesoscale eddies (e.g., Huang et al., 2022a).
 Figure 1. Identification of nonlinear internal waves (NLIWs) in the global ocean using 250 m resolution MODIS satellite observations from the Terra and Aqua missions of the Earth Observing System of National Aeronautics and Space Administration (NASA) from 2002 to 2004 (Jackson, 2007). The yellow shaded region shows the northeast South China Sea (SCS).
Figure 1. Identification of nonlinear internal waves (NLIWs) in the global ocean using 250 m resolution MODIS satellite observations from the Terra and Aqua missions of the Earth Observing System of National Aeronautics and Space Administration (NASA) from 2002 to 2004 (Jackson, 2007). The yellow shaded region shows the northeast South China Sea (SCS).When NLIWs shoal into shallower water, their waveforms, polarities, and vertical modes undergo changes, which lead to wave breaking and turbulence dissipation. These processes have been validated through in-situ observations (Ramp et al., 2004) and numerical simulations (Qian et al., 2015). Based on satellite images and ship-based observations in the SCS, polarity conversion from depression to elevation of NLIWs frequently occur at around 150–180 m isobaths during shoaling (Zhao et al., 2004; Orr and Mignerey, 2003). Mooring observations further confirm that the depression-type NLIWs significantly broaden along with formation of the trailing elevation waves (Duda et al., 2004). The elevation-type NLIWs are more prone to break, resulting in enhanced turbulent mixing (Klymak and Moum, 2003; Bourgault et al., 2007).
Shoaling NLIWs also exhibit multimode structures in vertical. Results from numerical simulation suggest that mode-2 NLIWs are preferentially formed under a deeper pycnocline during the shoaling process (Chen et al., 2014; Qian et al., 2015). Mode-2 NLIWs during the shoaling process have been frequently observed on the upper continental slope, which are argued to be generated by mode-1 NLIWs and stratification adjustments (Yang et al., 2009). Although weaker in kinetic energy, mode-2 NLIWs have larger vertical shear compared to mode-1 NLIWs, thus inducing stronger mixing (Qian et al., 2015).
Enhanced diapycnal mixing occurs during the shoaling process of NLIWs, exhibiting significantly elevated turbulent dissipation rate of O (10−6 W/kg to 10−4 W/kg) that surpass background levels by approximately two orders of magnitude (e.g., Zhang and Alford, 2015; Chang et al, 2021a; Moum et al., 2007; Lien et al., 2014). The enhanced mixing associated with NLIWs potentially plays an important role in sediment resuspension and transport. The resuspended sediment is upwelled into the water column interior and transported laterally, forming nepheloid layers (Reeder et al., 2011; Tian et al., 2021). As a result, NLIWs shape the seafloor by erosion caused by resuspension and deposition resulting from sediment accumulation such as sand waves and sediment gravity flows (Ma et al., 2016; Droghei et al., 2016).
This paper focuses on investigating the variations in NLIWs characteristics such as energy dissipation, shear instability levels across different vertical modes and polarities. Specifically, it explores instabilities of NLIWs as well as their interactions with topography leading to sediment resuspension, transportation, and seafloor deformation. This review incorporates field observations, theoretical analyses, laboratory experiments, and numerical simulations to enhance our knowledge regarding NLIW-triggered instability and sedimentary dynamics processes. Although due to observational limitations, literature discussions have primarily focused on specific regions with strong NLIWs such as the SCS, this review will provide a global perspective given the widespread nature of the generation, propagation, and shoaling processes of NLIWs.
2. Basic characteristics of nonlinear internal waves
Recently, long-term satellite observations have confirmed that NLIWs are ubiquitous oceanic processes in the global oceans. NLIWs alter sea surface roughness by producing divergent and convergent flow with sub-surface wave troughs and crests (e.g., Ouchi and Yoshida, 2023). This results in alternating dark and bright stripes in satellite imagery, which allows for remote sensing of NLIWs. More than
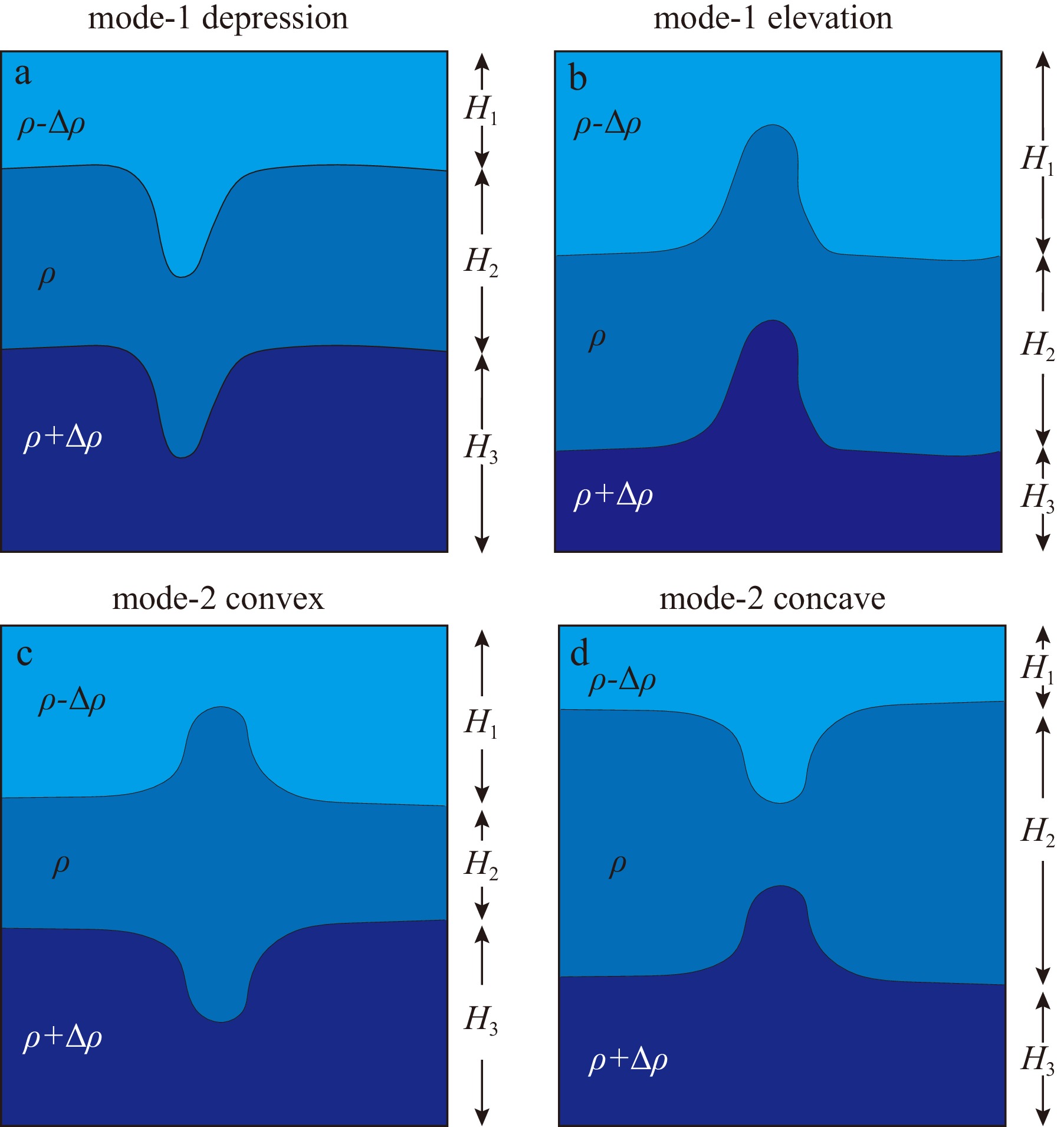
3500 NLIWs were detected globally through MODIS sunlight imagery with a spatial resolution of 250 m during August 2002 to May 2004 (Jackson, 2007; Fig. 1), revealing that well-known sites, activity areas, and expanded areas of NLIWs are primarily located near the coasts. The northeast SCS is one such well-known site with energetic NLIWs.In-situ observations reveal that baroclinic modes primarily manifest as vertical bending patterns of thermoclines (pycnoclines). Mode-1 NLIWs, characterized by pycnocline displaced towards the same directions throughout the whole water column, are frequently observed in nature (e.g., Huang et al., 2016). On the other hand, mode-2 NLIWs, inducing opposite displacements of isotherm in the upper and lower layers, are less commonly observed and are believed to form locally in shallow waters (e.g., Yang et al., 2009, 2010). Polarity reversal frequently occurs during shoaling when pycnoclines display reversed bending directions. For mode-1 NLIWs, polarity conversion occurs when they transition from depression (downward pycnocline displacement) to elevation (upward pycnocline displacement) (Li et al., 2015; Zhang et al., 2018; Figs 2a and b). For mode-2 NLIWs, polarity conversion occurs when they transform from convex-shaped bulges to concave-shaped constrictions within the pycnocline (Yang et al., 2010; Figs 2c and d).
 Figure 2. Sketch diagrams of mode-1 (depression and elevation) and mode-2 (convex and concave) nonlinear internal waves within a three-layer fluid structures [revised according to Kurkina et al., 2015 and Yang et al. (2010)].
Figure 2. Sketch diagrams of mode-1 (depression and elevation) and mode-2 (convex and concave) nonlinear internal waves within a three-layer fluid structures [revised according to Kurkina et al., 2015 and Yang et al. (2010)].Theoretical frameworks elucidate the phenomenon of polarity conversion and multimodal structures during the shoaling process of NLIWs. According to Korteweg–de Vries (KdV) theory, for mode-1 NLIWs, as internal waves propagate shoreward and encounter a decrease in water depth, a critical depth is reached where the nonlinear coefficient changes sign from negative to positive, resulting in polarity reversal (e.g., Benjamin, 1966; Liu et al., 1998). Studies have also revealed that multiscale processes such as internal tides, mesoscale eddies, and seasonal variations in stratification modulate the polarity conversion of mode-1 NLIWs (Zhang et al., 2018). For mode-2 NLIWs, theoretical analysis suggests that they can be generated from mode-1 NLIWs when a deep pycnocline lies near mid-depth during their shoaling (Yang et al., 2009). In terms of polarity characteristics, mode-2 NLIWs can be theoretically described by a three-layer model (e.g., Yang et al., 2010), with a thin (thick) middle layer leading to convex (concave) NLIWs (Figs 2c and d).
3. Instability of nonlinear internal wave
3.1 Instability theory
The wave deformation, polarity conversion and multimodal structures of NLIWs induce variations in vertical structures, leading to flow instabilities. Lamb (2014) described four mechanisms for the instability of NLIWs: shear instability, convective instability, bottom boundary layer (BBL) instability, and wave breaking during shoaling at abrupt topography. Among these mechanisms, shear instability and convective instability have been supported by the most observational evidence (e.g., Moum et al., 2003; Chang et al., 2021a).
Shear instability occurs when the vertical shear (S2) of horizontal velocity overcomes stratification (N2). Shear instability is therefore quantified by the Gradient Richardson number Ri =N2/S2. Generally, shear instability occurs when Ri < 1/4 (Miles, 1961), although this criterion can be more stringent for NLIWs (Chang et al., 2021a). In the case of mode-1 depression NLIWs, shear instability tends to occur near the wave trough where large vertical shear is present (Fig. 3a). Observational evidence includes overturns and Kelvin–Helmholtz billows (Moum et al., 2003; Fig. 3c). The billows develop near the wave troughs and extend towards the trailing edges, corresponding to enhanced turbulence (Figs 3c and e). Convective instability occurs when wave-induced horizontal velocity (U) exceeds phase speed (C) and typically manifests near the wave core where stratification is weak (Fig. 3b). This type of instability also gives rise to overturns and leads to a distinctive structure known as trapped cores, leading to enhanced turbulence emerging from the core towards the trailing edges (e.g., Chang et al., 2021a; Fig. 3f).
 Figure 3. Instability mechanisms for mode-1 depression nonlinear internal waves. a. Shear instability and b. convective instability [revised according to Lamb (2014)]. Type of instability and its position are for the mode-1 depression NLIW with rightward phase speed C and horizontal velocity U. c. Kelvin-Helmholtz billows driven by shear instability [revised according to Moum et al. (2003)]. d. Trapped cores driven by convective instability. The simulated trapped core is exhibited in the left corner [revised according to Chang et al. (2021a) and Rivera-Rosario et al. (2020)]. e and f. Dissipation rate of shear instability and convective instability [revised according to Zhang and Alford (2015)].
Figure 3. Instability mechanisms for mode-1 depression nonlinear internal waves. a. Shear instability and b. convective instability [revised according to Lamb (2014)]. Type of instability and its position are for the mode-1 depression NLIW with rightward phase speed C and horizontal velocity U. c. Kelvin-Helmholtz billows driven by shear instability [revised according to Moum et al. (2003)]. d. Trapped cores driven by convective instability. The simulated trapped core is exhibited in the left corner [revised according to Chang et al. (2021a) and Rivera-Rosario et al. (2020)]. e and f. Dissipation rate of shear instability and convective instability [revised according to Zhang and Alford (2015)].During the shoaling process of NLIWs, the mechanisms triggering instability vary for different wave types under various bottom topographies (Fig. 4). Under a flat bottom, mode-1 depression NLIWs can generate a jet with shear instabilities at their trailing edge due to an unbalanced NLIW-induced pressure gradient in the BBL (Diamessis and Redekopp, 2006; Fig. 4a). The background and NLIW-induced currents are shown in Fig. 4c. In contrast, for mode-1 elevation NLIWs, instability occurs near the front of the wave (Stastna and Lamb, 2008), leading to vortices being ejected from the BBL into the upper water and forming a separating bubble (Figs 4b and d). This scenario described above has been validated through observation conducted by Moum et al. (2007).
 Figure 4. Schematic diagrams of instability mechanisms for mode-1 depression and elevation nonlinear internal waves (NLIWs) over flat bottom and slope during shoaling (revised according Boegman and Stastna, 2019). a and b. Instability and current of mode-1 depression NLIW. c and d. Instability and current of mode-1 elevation NLIW. e. Instability of the shoaling NLIW. f. Instability of the upslope-propagating boluses.
Figure 4. Schematic diagrams of instability mechanisms for mode-1 depression and elevation nonlinear internal waves (NLIWs) over flat bottom and slope during shoaling (revised according Boegman and Stastna, 2019). a and b. Instability and current of mode-1 depression NLIW. c and d. Instability and current of mode-1 elevation NLIW. e. Instability of the shoaling NLIW. f. Instability of the upslope-propagating boluses.When mode-1 depression NLIWs propagate over a slope during shoaling, the waveform becomes asymmetrical, forming a steeper rear trailing (Fig. 4e). Numerical simulations [e.g. Aghsaee et al. (2012)] provide visualizations of elevation waves generated from polarity reversion of depression waves at the turning point, generating upslope-propagating boluses that induce turbulence in the BBL (Fig. 4f). The existence of such boluses along slope has been validated through numerical simulations [e.g., Arthur and Fringer (2014)], laboratory experiments [e.g., Boegman and lvey (2009)], and in-situ observations [e.g., Hosegood et al. (2004)].
3.2 Observation of NLIW-induced instability
Numerous in-situ observations have revealed the existence of shear instability and convective instability within different types (polarities and modes) of shoaling NLIWs. For mode-1 depression NLIWs, Moum et al. (2003) observed Kelvin–Helmholtz billows driven by shear-induced instabilities originating from wave troughs and extending towards their trailing edges. Zhang and Alford (2015) observed enhanced turbulent dissipation rate within the steeper trailing edges of the shoaling NLIWs accordant with theory (Figs 4e, 5a and b). Huang et al. (2022a) observed overturns induced by shear-driven turbulence at both edges of depression NLIWs in the SCS, shedding light on the regulations imposed by multiscale processes. In addition, Chang et al. (2021a) demonstrated that convective instabilities occur during their shoaling in the SCS, leading to the splitting of NLIWs into trailing waves (Chang et al., 2021b).
For mode-1 elevation NLIWs, Orr and Mignerey (2003) observed billow-like overturns exceeding 100 m in the northern SCS when mode-1 depression NLIWs transform into mode-1 elevation waves. Moum et al. (2007) observed elevated dissipation rate near the steepened leading edges of the elevation waves (Fig. 5c). In a recent study, Jones et al. (2020) observed intense overturns and diapycnal mixing resulting from the coexistence of shear-driven and convective-induced instabilities within shoaling elevation NLIWs, accompanied by enhanced diapycnal mixing (> 10−3 m2/s1), heat flux (> 500 W/m2), and overturns predominantly occurring at the steeper wave edges (Figs 5d and e), which corresponds with the theoretical framework presented in Figs 4b-f.
 Figure 5. In-situ observations of the instability induced by shoaling nonlinear internal waves (NLIWs). a and b. Instability of mode-1 depression NLIWs with steeper trailing edges [revised according to Zhang and Alford (2015)]. c and e. Instability of mode-1 elevation NLIWs with steeper leading edges [revised according to Klymak and Moum (2003) and Jones et al. (2020)].
Figure 5. In-situ observations of the instability induced by shoaling nonlinear internal waves (NLIWs). a and b. Instability of mode-1 depression NLIWs with steeper trailing edges [revised according to Zhang and Alford (2015)]. c and e. Instability of mode-1 elevation NLIWs with steeper leading edges [revised according to Klymak and Moum (2003) and Jones et al. (2020)].Instabilities associated with mode-2 NLIW are rarely documented in the literature. Whitwell et al. (2024) observed turbulence mixing induced by mode-2 convex NLIWs, revealing that intense mixing predominantly occurs along the steepened fronts where vertical shear is pronounced, while the central region remains relatively quiescent.
Convective instability and shear instability also interact with each other. Chang et al. (2021a) observed that most of NLIWs exhibit convective instability, but only a small portion display notable convective features of trapped cores. They proposed that shear instability suppresses the occurrence of convection due to that Kelvin–Helmholtz billows, hindering the plunging of cold-water and the formation of trapped core. By contrast, convective instability can promote shear instability. In specific, convective overturns enhance isopycnal compression, which strengthens vertical shear an order of magnitude larger than stratification, thus enhancing shear instability. This conclusion is validated by observations by Moum et al. (2003) and Carr et al. (2008, 2012).
4. Sediment response to nonlinear internal waves
The instability during the shoaling process of NLIWs is supposed to correlate with intense sedimentary dynamics. We herein examine the sedimentary processes induced by NLIWs across three sequential stages: sediment resuspension, transportation, and seafloor deformation. Considering the complexity of sediment responses to variable NLIWs, here we focus on the in-situ observations to sum up the basic sedimentary dynamics.
4.1 Sediment resuspension
Many observations have demonstrated that the peak suspended sediment concentration (SSC) typically occurs at the trailing edge of depression NLIWs, accompanied by strong convergent bottom currents (Bogucki et al., 1997; Johnson et al., 2001; Carter et al., 2005). In specific reference to the SCS, Reeder et al. (2011) reported a nepheloid layer extending up to 200 m due to vigorous sediment suspension. Jia et al. (2019) observed that NLIW-induced sediment resuspension on the shelf of SCS, identifying and estimating an annual sediment resuspension rate of approximately 787 million tons caused by NLIWs.
Highly-resolved observations in the BBL reveal that sediment resuspension is primarily controlled by the combined effects of intensified bed‐stress, turbulent dissipation rate, and vertical pumping (Zulberti et al., 2020). The entire process can be divided into three stages (Figs 6a and b): (1) prior to wave arrival, flow acceleration leads to increased velocity shear, intensified turbulence and sediment resuspension; (2) beneath the wave trough, sediment concentration across the mixing‐layer is the maximum owing to enhanced transport before wave arrival and a thinner mixing‐layer compressed by NLIWs; (3) following the trough, sediments are rapidly dispersed as the mixed-layer expands from rising isotherms.
 Figure 6. In-situ observations of sediment resuspension by nonlinear internal waves. a and b. Sediment resuspension by mode-1 depression NLIWs [revised according to Zulberti et al. (2020)]. c. Sediment resuspension by mode-1 elevation NLIWs [revised according to Klymak and Moum (2003)].
Figure 6. In-situ observations of sediment resuspension by nonlinear internal waves. a and b. Sediment resuspension by mode-1 depression NLIWs [revised according to Zulberti et al. (2020)]. c. Sediment resuspension by mode-1 elevation NLIWs [revised according to Klymak and Moum (2003)].Shoaling processes of mode-1 elevation NLIWs are typically characterized by both a turbulent trapped core and increased optical backscatter, which is an indicator for elevated sediment concentration (Klymak and Moum, 2003; Fig. 6c). Further studies on elevation NLIWs indicate that sediment resuspension occurs at high-density front near the bottom along the wave’s edge (Scotti and Pineda, 2004; Moum et al., 2007).
Sediment resuspension induced by mode-2 NLIWs is rarely observed. Bogucki et al. (1997) reported elevated SSC near the bottom, attributed to vortex structures resulting from variation of current structures induced by the passage of mode-2 NLIWs. Despite some existing observations, there remains a dearth of comprehensive and highly-resolved studies in the BBL, which are essential for elucidating sediment resuspension mechanisms and different stages of sediment response to a passing NLIW.
4.2 Sediment transportation
When bottom sediment is resuspended, coarse particles settle while fine particles are laterally transported, forming an intrusive nepheloid layer that contains a higher concentration of suspended particles compared to the surrounding water. Nepheloid layers primarily consist of the intermediate nepheloid layer (INL) and bottom nepheloid layer (BNL). These layers serve as crucial conduits for both terrestrial sediment transport to the seafloor and transportation of suspended particles from the ocean margin to its basin. Both field observations (Cheriton et al., 2014; Johnson et al., 2001; Quaresma et al., 2007) and numerical simulations (Bourgault et al., 2014) have validated that vertical velocities and pumping near the bottom induced by NLIWs play a predominant role in driving INL and BNL on the continental slope and shelf.
The scale of NLIW-induced nepheloid layer varies, typically extending vertically from tens of meters to hundreds of meters. Moum et al. (2007) observed nepheloid layer thickness ranging approximately 10–50 m on the Oregon shelf triggered by elevation NLIWs. Jia et al. (2019) documented at least four BNLs with thicknesses ranging from 70 m to 140 m on the SCS shelf, which were attributed to NLIWs.
Recent studies reveal that the formation and characteristics of BNL and INL are determined by the relationship between angle of NLIW’s group velocity (α) and slope gradient (γ) [e.g., Tian et al. (2021)]. Puig et al. (2004) redefined α as:
$$ \alpha = {\mathrm{arctan}} \left[{\left(\frac{{{\sigma ^2} - {f^2}}}{{{N^2} - {\sigma ^2}}}\right)^{1/2}}\right], $$ (1) where
$ \sigma $ is frequency of internal wave,$ f $ is local inertial frequency, and N is buoyancy frequency. In transmissive regions (γ/α < 1), where energy propagates between seafloor and the pycnocline, a single BNL and several weaker INLs may emerge between the pycnocline and the seafloor (Fig. 7a). These findings are supported by observations (Masunaga et al., 2017; Richards et al., 2013; Hosegood et al., 2004), which report BNL thicknesses of approximately 2 m, 5 m, and 100 m, respectively. Under such circumstances, Tian et al. (2019) demonstrate that sediment is initially suspended by horizontal velocity before being lifted into water column by vertical velocity (Fig. 7b). Figure 7. Schematic diagrams of the formation of bottom nepheloid layer (BNL) and intermediate nepheloid layer (INL) by shoaling nonlinear internal waves (NLIWs) in transmissive regions (revised according to [Tian et al. (2019)]. a. One BNL and multiple INLs formed from shoaling depression NLIWs. α is group velocity vector of NLIWs, γ is slope gradient, and γ/α < 1 means transmissive regions. b. Resuspension process by shoaling NLIWs on the slope. Sediment is first resuspended by horizontal velocity (①), and then lifted by vertical velocity into the water column (②).
Figure 7. Schematic diagrams of the formation of bottom nepheloid layer (BNL) and intermediate nepheloid layer (INL) by shoaling nonlinear internal waves (NLIWs) in transmissive regions (revised according to [Tian et al. (2019)]. a. One BNL and multiple INLs formed from shoaling depression NLIWs. α is group velocity vector of NLIWs, γ is slope gradient, and γ/α < 1 means transmissive regions. b. Resuspension process by shoaling NLIWs on the slope. Sediment is first resuspended by horizontal velocity (①), and then lifted by vertical velocity into the water column (②).In critical regions (γ/α~1), where energy of NLIWs dissipates at a single point, only one BNL was observed. In this case, the thickness of BNL is the maximum due to the most energetic phase of NLIWs. This is supported by an observed BNL with 200 m thickness in the shelf break of SCS, where is a critical region (Reeder et al., 2011). In reflective regions (γ/α > 1), where most energy from NLIW is reflected back into the ocean, BNL or INL was seldom observed. However, formation mechanisms of BNL and INL under different types of NLIWs remain unclear.
4.3 Seafloor deformation
Recent studies reveal that NLIW-induced resuspension/transport is intense enough to reshape the topography, deforming original flat seafloor into structures such like sand/sediment waves and scour channels. Observed NLIW-induced sand waves off the Messina Strait, covering an area about 3 km2, with wavelengths of 60–120 m and wave heights of 1.5–5 m, are perpendicular to the propagation direction of NLIWs (Droghei et al., 2016). Meantime, larger-scale and finer-grained sediment waves are also found on continental slope area related to internal wave, validated by sparker seismic observations on the Landes Plateau in the North Atlantic (Faugères et al., 2002) and in the slopes of the Gulf of Valencia (Ribó et al., 2016). Additionally, erosion features of short scour channels were observed on the seafloor, which is attributed to along-slope current of NLIWs (Ma et al., 2016).
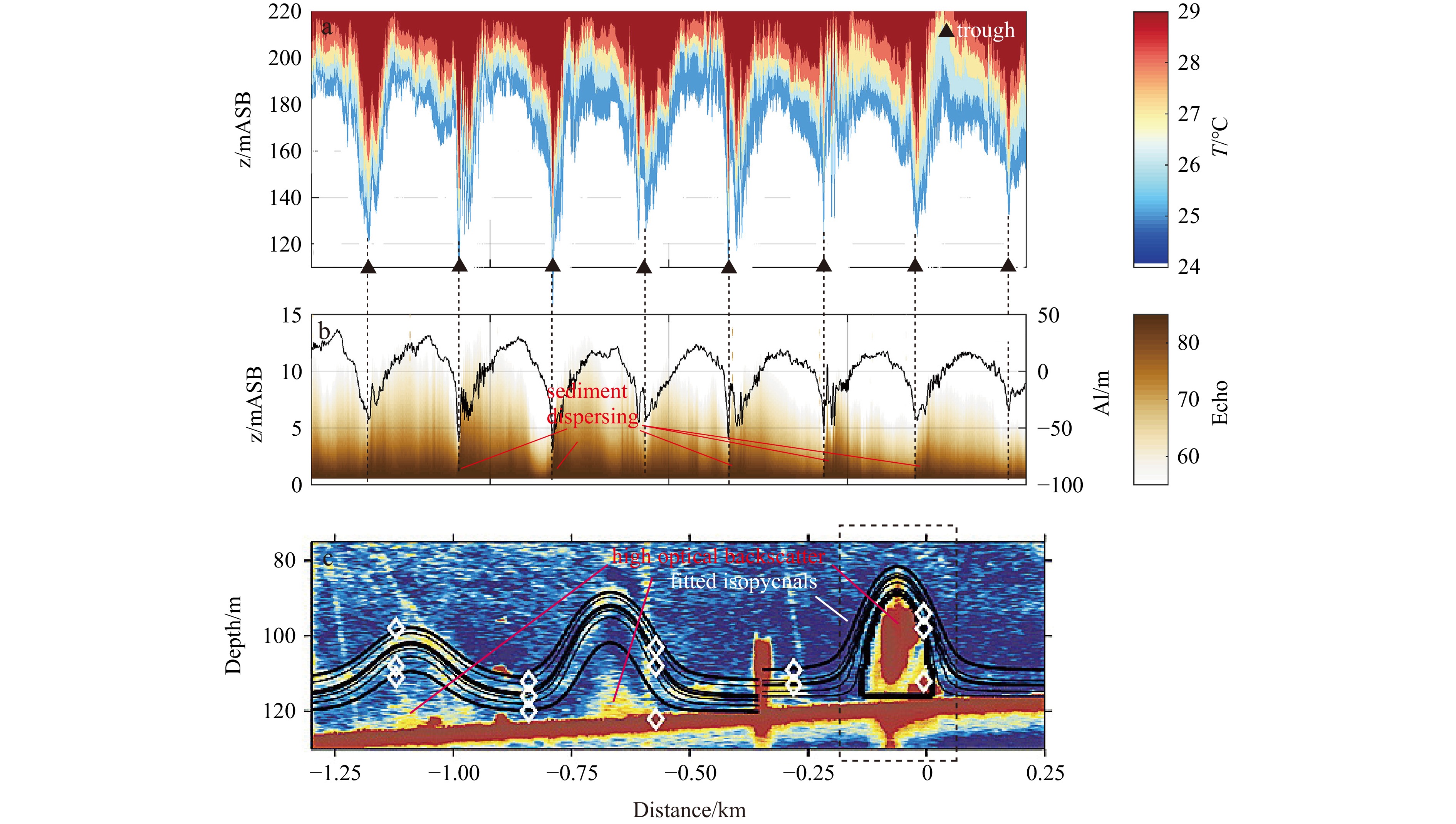
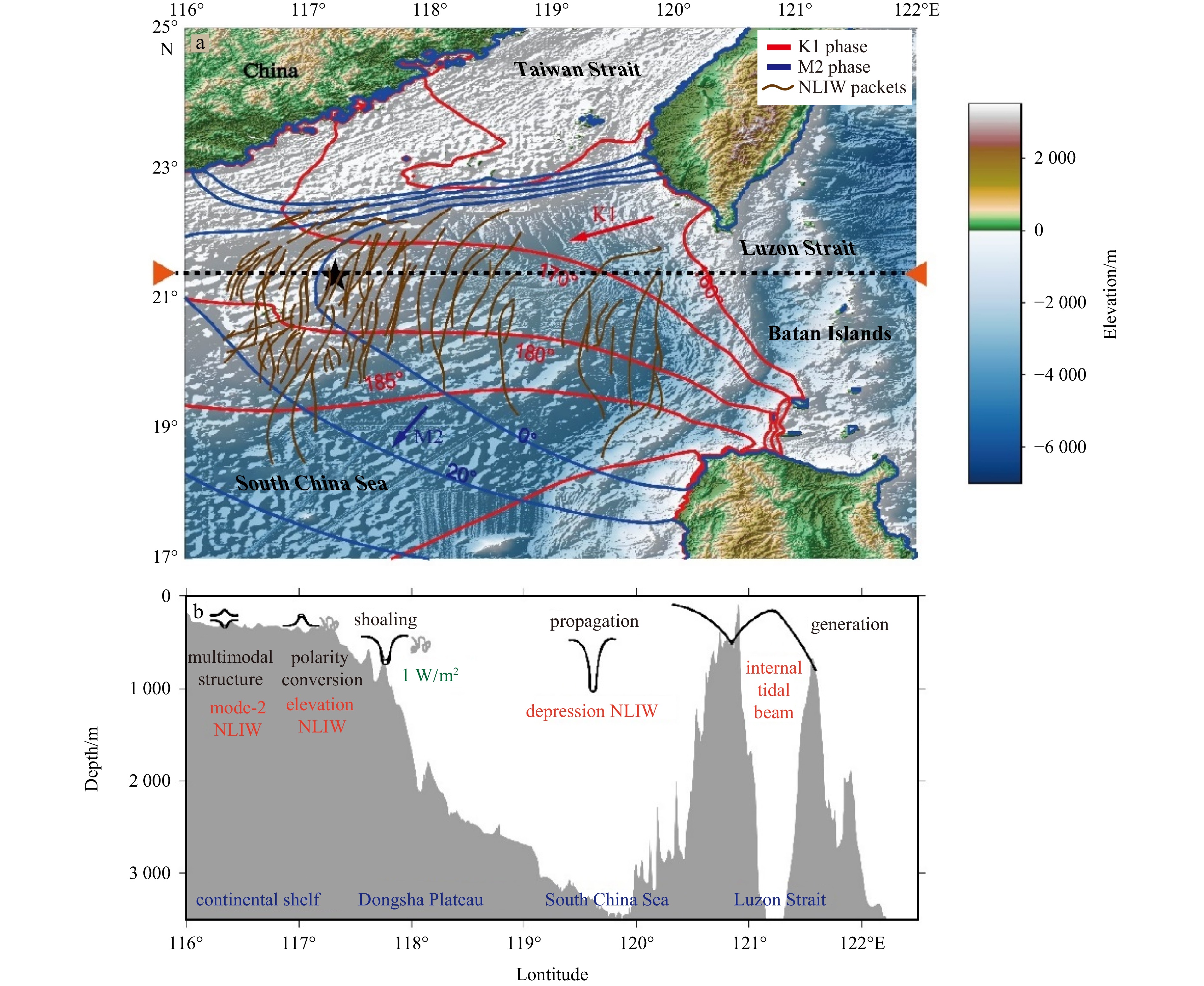
The northeast SCS is renowned for hosting the most energetic NLIWs in the global ocean, making it an ideal region for investigating NLIW-triggered sediment response and bed deformation. Four observational programs, namely ASIAEX, VANS/WISE, NLIWI, and IWISE, have been implemented in the SCS to shed light on the generation, propagation, shoaling and turbulence dissipation of NLIWs (e.g., Guo and Chen, 2014; Alford et al., 2015). Mode-1 dominant NLIWs prevail in the SCS and primarily generated through nonlinear steepening of internal tides, which originate from tide-topography interactions near Luzon Strait (Fig. 8a). As they propagate approximately 400 km westward onto the shelf during the shoaling process, mode-1 depression NLIWs undergo waveform deformation and polarity conversion, leading to multimodal structures (Yang et al., 2009, 2010; Chen et al., 2019). These intense energy dissipating NLIWs induce significant sediment response on the continental slope, with maximum depth-integrated dissipation rate reaching about 1 W/m2 over the uppermost 250 m during their shoaling onto the Dongsha Plateau (Chang et al., 2006; St Laurent et al., 2011; Fig. 8b).
 Figure 8. Nonlinear internal waves (NLIWs) in the northeast South China Sea (SCS). a. Packets of NLIWs observed in satellite images acquired from 1995 to 2001 in the SCS [revised according to Zhao et al. (2004)]. Barotropic tidal phases are marked for K1 (M2) components by red (blue) solid lines, when numbers represent phase angles. b. Sketch diagram of NLIWs evolution in the SCS including generation, propagation, shoaling, and turbulence dissipation, turbulence processes are presented by vortices in gray, the maximum depth-integrated dissipation rate is marked to the Dongsha Plateau [revised according to St Laurent et al. (2011)].
Figure 8. Nonlinear internal waves (NLIWs) in the northeast South China Sea (SCS). a. Packets of NLIWs observed in satellite images acquired from 1995 to 2001 in the SCS [revised according to Zhao et al. (2004)]. Barotropic tidal phases are marked for K1 (M2) components by red (blue) solid lines, when numbers represent phase angles. b. Sketch diagram of NLIWs evolution in the SCS including generation, propagation, shoaling, and turbulence dissipation, turbulence processes are presented by vortices in gray, the maximum depth-integrated dissipation rate is marked to the Dongsha Plateau [revised according to St Laurent et al. (2011)].In the recent study, Tian et al. (2021) present a comprehensive depiction of sediment response to NLIWs in the SCS. They argue that NLIWs induce strong sediment resuspension and shape bedforms at water depths less than
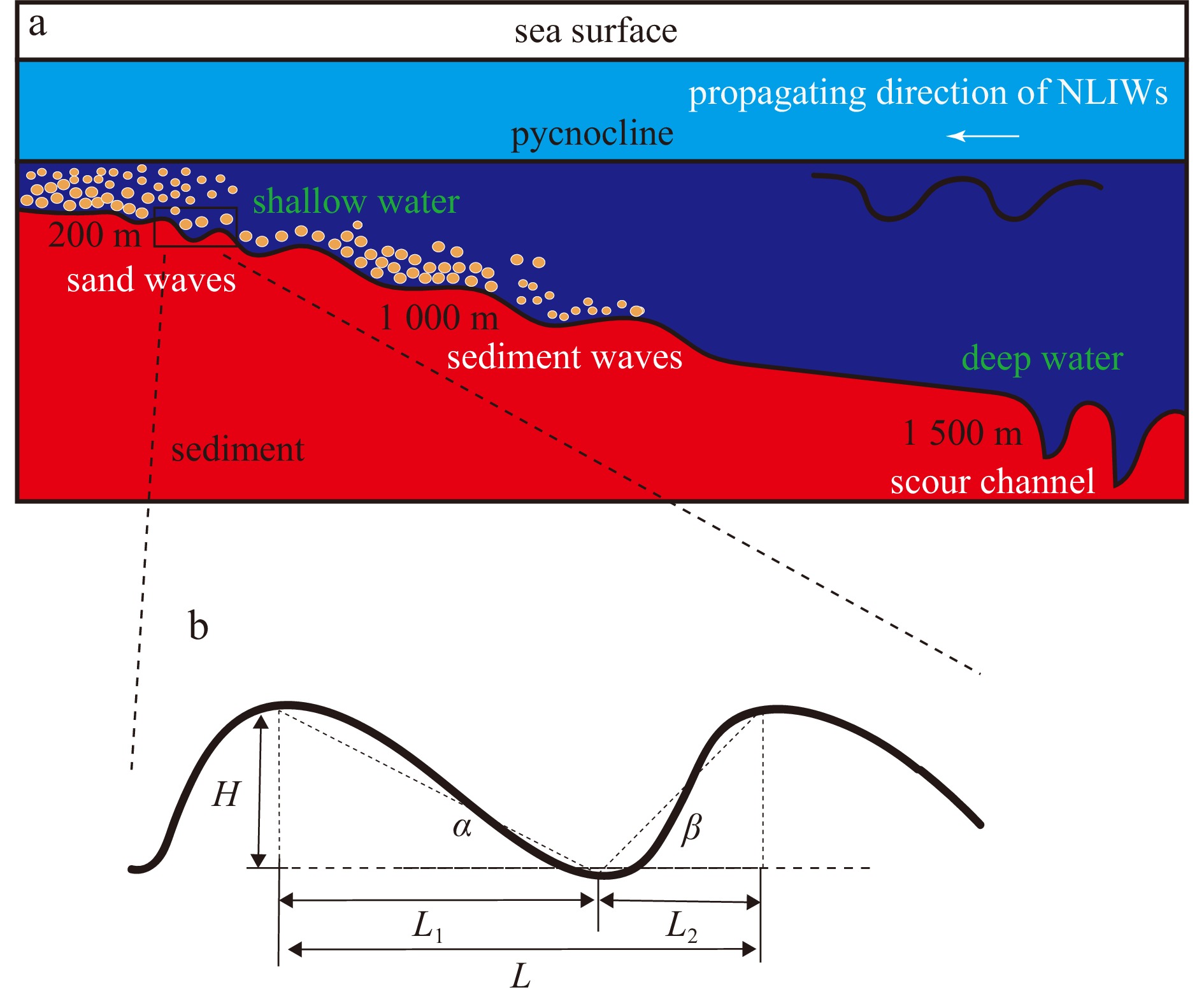
1000 m, resulting in the formation of sand waves and sediment waves (Fig. 9a). In the meantime, scour channels are formed at deeper depth exceeding1500 m. These NLIW-induced asymmetrical sand waves exhibit upslope-dipping characteristics with larger northwestern flanks (L1) compared to southeastern flanks (L2), accompanied by corresponding gentle slopes (α) towards the northwest direction (Fig. 9b). Furthermore, they have also found that NLIWs in the SCS lead to tilt, upslope and downslope migration of sand waves (Miramontes et al., 2020). Figure 9. Schematic diagrams of seafloor transformation by nonlinear internal waves (NLIWs). a. Sediment resuspension and bedforms of sand waves, scour channels and sediment waves on the slope [revised according to Tian et al. (2021)]. b. Profile of the asymmetrical sand waves. Parameters of wave height H, wavelength L, project length of the gentle slope L1, and project length of the steep slope L2, angle of gentle slope α (H/L1), angle of steep slope β (H/L2) are marked.
Figure 9. Schematic diagrams of seafloor transformation by nonlinear internal waves (NLIWs). a. Sediment resuspension and bedforms of sand waves, scour channels and sediment waves on the slope [revised according to Tian et al. (2021)]. b. Profile of the asymmetrical sand waves. Parameters of wave height H, wavelength L, project length of the gentle slope L1, and project length of the steep slope L2, angle of gentle slope α (H/L1), angle of steep slope β (H/L2) are marked.5. Summary and outlook
Numerical simulation, laboratory experiment, and in-situ observations have significantly contributed to the fundamental understanding of the flow instabilities induced by NLIWs and their impact on sediment responses. However, several unresolved issues still necessitate further investigation. To establish quantitative relationships between the NLIWs and sediment transport as well as deposition/erosion, it is crucial to investigate the interplay between shear instability and convective instability, along with the instability patterns of NLIWs under multiscale processes. Current observations lack the ability to differentiate resuspension patterns caused by different types of NLIWs, particularly mode-2 NLIWs which are transient and challenging to capture. Therefore, there is a need for quantitative investigations into how NLIWs generate nepheloid layers and reshape bedforms effectively. In order to address these issues adequately, long-term and highly-resolved in-situ observations within the bottom boundary layer are essential.
-
Figure 1. Identification of nonlinear internal waves (NLIWs) in the global ocean using 250 m resolution MODIS satellite observations from the Terra and Aqua missions of the Earth Observing System of National Aeronautics and Space Administration (NASA) from 2002 to 2004 (Jackson, 2007). The yellow shaded region shows the northeast South China Sea (SCS).
Figure 2. Sketch diagrams of mode-1 (depression and elevation) and mode-2 (convex and concave) nonlinear internal waves within a three-layer fluid structures [revised according to Kurkina et al., 2015 and Yang et al. (2010)].
Figure 3. Instability mechanisms for mode-1 depression nonlinear internal waves. a. Shear instability and b. convective instability [revised according to Lamb (2014)]. Type of instability and its position are for the mode-1 depression NLIW with rightward phase speed C and horizontal velocity U. c. Kelvin-Helmholtz billows driven by shear instability [revised according to Moum et al. (2003)]. d. Trapped cores driven by convective instability. The simulated trapped core is exhibited in the left corner [revised according to Chang et al. (2021a) and Rivera-Rosario et al. (2020)]. e and f. Dissipation rate of shear instability and convective instability [revised according to Zhang and Alford (2015)].
Figure 4. Schematic diagrams of instability mechanisms for mode-1 depression and elevation nonlinear internal waves (NLIWs) over flat bottom and slope during shoaling (revised according Boegman and Stastna, 2019). a and b. Instability and current of mode-1 depression NLIW. c and d. Instability and current of mode-1 elevation NLIW. e. Instability of the shoaling NLIW. f. Instability of the upslope-propagating boluses.
Figure 5. In-situ observations of the instability induced by shoaling nonlinear internal waves (NLIWs). a and b. Instability of mode-1 depression NLIWs with steeper trailing edges [revised according to Zhang and Alford (2015)]. c and e. Instability of mode-1 elevation NLIWs with steeper leading edges [revised according to Klymak and Moum (2003) and Jones et al. (2020)].
Figure 6. In-situ observations of sediment resuspension by nonlinear internal waves. a and b. Sediment resuspension by mode-1 depression NLIWs [revised according to Zulberti et al. (2020)]. c. Sediment resuspension by mode-1 elevation NLIWs [revised according to Klymak and Moum (2003)].
Figure 7. Schematic diagrams of the formation of bottom nepheloid layer (BNL) and intermediate nepheloid layer (INL) by shoaling nonlinear internal waves (NLIWs) in transmissive regions (revised according to [Tian et al. (2019)]. a. One BNL and multiple INLs formed from shoaling depression NLIWs. α is group velocity vector of NLIWs, γ is slope gradient, and γ/α < 1 means transmissive regions. b. Resuspension process by shoaling NLIWs on the slope. Sediment is first resuspended by horizontal velocity (①), and then lifted by vertical velocity into the water column (②).
Figure 8. Nonlinear internal waves (NLIWs) in the northeast South China Sea (SCS). a. Packets of NLIWs observed in satellite images acquired from 1995 to 2001 in the SCS [revised according to Zhao et al. (2004)]. Barotropic tidal phases are marked for K1 (M2) components by red (blue) solid lines, when numbers represent phase angles. b. Sketch diagram of NLIWs evolution in the SCS including generation, propagation, shoaling, and turbulence dissipation, turbulence processes are presented by vortices in gray, the maximum depth-integrated dissipation rate is marked to the Dongsha Plateau [revised according to St Laurent et al. (2011)].
Figure 9. Schematic diagrams of seafloor transformation by nonlinear internal waves (NLIWs). a. Sediment resuspension and bedforms of sand waves, scour channels and sediment waves on the slope [revised according to Tian et al. (2021)]. b. Profile of the asymmetrical sand waves. Parameters of wave height H, wavelength L, project length of the gentle slope L1, and project length of the steep slope L2, angle of gentle slope α (H/L1), angle of steep slope β (H/L2) are marked.
-
Aghsaee P, Boegman L, Diamessis P J, et al. 2012. Boundary-layer-separation-driven vortex shedding beneath internal solitary waves of depression. Journal of Fluid Mechanics, 690: 321–344, doi: 10.1017/jfm.2011.432 Alford M H, Peacock T, MacKinnon J A, et al. 2015. The formation and fate of internal waves in the South China Sea. Nature, 521(7550): 65–69, doi: 10.1038/nature14399 Arthur R S, Fringer O B. 2014. The dynamics of breaking internal solitary waves on slopes. Journal of Fluid Mechanics, 761: 360–398, doi: 10.1017/jfm.2014.641 Benjamin T B. 1966. Internal waves of finite amplitude and permanent form. Journal of Fluid Mechanics, 25(2): 241–270, doi: 10.1017/S0022112066001630 Boegman L, Ivey G N. 2009. Flow separation and resuspension beneath shoaling nonlinear internal waves. Journal of Geophysical Research: Oceans, 114(C2): C02018 Boegman L, Stastna M. 2019. Sediment resuspension and transport by internal solitary waves. Annual Review of Fluid Mechanics, 51(1): 129–154, doi: 10.1146/annurev-fluid-122316-045049 Bogucki D, Dickey T, Redekopp L G. 1997. Sediment resuspension and mixing by resonantly generated internal solitary waves. Journal of Physical Oceanography, 27(7): 1181–1196, doi: 10.1175/1520-0485(1997)027<1181:SRAMBR>2.0.CO;2 Bourgault D, Blokhina M D, Mirshak R, et al. 2007. Evolution of a shoaling internal solitary wavetrain. Geophysical Research Letters, 34(3): L03601 Bourgault D, Morsilli M, Richards C, et al. 2014. Sediment resuspension and nepheloid layers induced by long internal solitary waves shoaling orthogonally on uniform slopes. Continental Shelf Research, 72: 21–33, doi: 10.1016/j.csr.2013.10.019 Carr M, Fructus D, Grue J, et al. 2008. Convectively induced shear instability in large amplitude internal solitary waves. Physics of Fluids, 20(12): 126601, doi: 10.1063/1.3030947 Carr M, King S E, Dritschel D G. 2012. Instability in internal solitary waves with trapped cores. Physics of Fluids, 24(1): 016601, doi: 10.1063/1.3673612 Carter G S, Gregg M C, Lien R C. 2005. Internal waves, solitary-like waves, and mixing on the Monterey Bay shelf. Continental Shelf Research, 25(12-13): 1499–1520, doi: 10.1016/j.csr.2005.04.011 Chang M H, Cheng Y H, Yang Y J, et al. 2021a. Direct measurements reveal instabilities and turbulence within large amplitude internal solitary waves beneath the ocean. Communications Earth & Environment, 2(1): 15 Chang M H, Lien R C, Lamb K G, et al. 2021b. Long-term observations of shoaling internal solitary waves in the northern South China Sea. Journal of Geophysical Research: Oceans, 126(10): e2020JC017129, doi: 10.1029/2020JC017129 Chang M H, Lien R C, Tang T Y, et al. 2006. Energy flux of nonlinear internal waves in northern South China Sea. Geophysical Research Letters, 33(3): L03607 Chen Liang, Zheng Quanan, Xiong Xuejun, et al. 2019. Dynamic and statistical features of internal solitary waves on the continental slope in the northern South China Sea derived from mooring observations. Journal of Geophysical Research: Oceans, 124(6): 4078–4097, doi: 10.1029/2018JC014843 Chen Zhiwu, Xie Jieshuo, Wang Dongxiao, et al. 2014. Density stratification influences on generation of different modes internal solitary waves. Journal of Geophysical Research: Oceans, 119(10): 7029–7046, doi: 10.1002/2014JC010069 Cheriton O M, McPhee-Shaw E E, Shaw W J, et al. 2014. Suspended particulate layers and internal waves over the southern Monterey Bay continental shelf: an important control on shelf mud belts?. Journal of Geophysical Research: Oceans, 119(1): 428–444, doi: 10.1002/2013JC009360 da Silva J C B, Helfrich K R. 2008. Synthetic aperture radar observations of resonantly generated internal solitary waves at Race Point Channel (Cape Cod). Journal of Geophysical Research: Oceans, 113(C11): C11016 Diamessis P J, Redekopp L G. 2006. Numerical investigation of solitary internal wave-induced global instability in shallow water benthic boundary layers. Journal of Physical Oceanography, 36(5): 784–812, doi: 10.1175/JPO2900.1 Droghei R, Falcini F, Casalbore D, et al. 2016. The role of internal solitary waves on deep-water sedimentary processes: the case of up-slope migrating sediment waves off the Messina Strait. Scientific Reports, 6(1): 36376, doi: 10.1038/srep36376 Duda T F, Lynch J F, Irish J D, et al. 2004. Internal tide and nonlinear internal wave behavior at the continental slope in the northern South China Sea. IEEE Journal of Oceanic Engineering, 29(4): 1105–1130, doi: 10.1109/JOE.2004.836998 Faugères J C, Gonthier E, Mulder T, et al. 2002. Multi-process generated sediment waves on the Landes Plateau (Bay of Biscay, North Atlantic). Marine Geology, 182(3–4): 279–302, doi: 10.1016/S0025-3227(01)00242-0 Guo C, Chen X. 2014. A review of internal solitary wave dynamics in the northern South China Sea. Progress in Oceanography, 121: 7–23, doi: 10.1016/j.pocean.2013.04.002 Hosegood P, Bonnin J, van Haren H. 2004. Solibore-induced sediment resuspension in the Faeroe-Shetland Channel. Geophysical Research Letters, 31(9): L09301 Huang Siwei, Huang Xiaodong, Zhao Wei, et al. 2022a. Shear instability in internal solitary waves in the northern South China Sea induced by multiscale background processes. Journal of Physical Oceanography, 52(12): 2975–2994, doi: 10.1175/JPO-D-21-0241.1 Huang Xiaodong, Chen Zhaohui, Zhao Wei, et al. 2016. An extreme internal solitary wave event observed in the northern South China Sea. Scientific Reports, 6(1): 30041, doi: 10.1038/srep30041 Huang Xiaodong, Huang Siwei, Zhao Wei, et al. 2022b. Temporal variability of internal solitary waves in the northern South China Sea revealed by long-term mooring observations. Progress in Oceanography, 201: 102716, doi: 10.1016/j.pocean.2021.102716 Hung J J, Wang Y H, Fu K H, et al. 2021. Biogeochemical responses to internal-wave impacts in the continental margin off Dongsha atoll in the northern South China Sea. Progress in Oceanography, 199: 102689, doi: 10.1016/j.pocean.2021.102689 Jackson C. 2007. Internal wave detection using the moderate resolution imaging spectroradiometer (MODIS). Journal of Geophysical Research: Oceans, 112(C11): C11012 Jackson C R, Da Silva J C B, Jeans G. 2012. The generation of nonlinear internal waves. Oceanography, 25(2): 108–123, doi: 10.5670/oceanog.2012.46 Jia Yonggang, Tian Zhuangcai, Shi Xuefa, et al. 2019. Deep-sea sediment resuspension by internal solitary waves in the northern South China Sea. Scientific Reports, 9(1): 12137, doi: 10.1038/s41598-019-47886-y Johnson D R, Weidemann A, Pegau W S. 2001. Internal tidal bores and bottom nepheloid layers. Continental Shelf Research, 21(13–14): 1473–1484, doi: 10.1016/S0278-4343(00)00109-6 Jones N L, Ivey G N, Rayson M D, et al. 2020. Mixing driven by breaking nonlinear internal waves. Geophysical Research Letters, 47(19): e2020GL089591, doi: 10.1029/2020GL089591 Klymak J M, Moum J N. 2003. Internal solitary waves of elevation advancing on a shoaling shelf. Geophysical Research Letters, 30(20): 2045 Klymak J M, Pinkel R, Liu C T, et al. 2006. Prototypical solitons in the South China Sea. Geophysical Research Letters, 33(11): L11607 Kurkina O E, Kurkin A A, Rouvinskaya E A, et al. 2015. Propagation regimes of interfacial solitary waves in a three-layer fluid. Nonlinear Processes in Geophysics, 22(2): 117–132, doi: 10.5194/npg-22-117-2015 Lamb K G. 2014. Internal wave breaking and dissipation mechanisms on the continental slope/shelf. Annual Review of Fluid Mechanics, 46(1): 231–254, doi: 10.1146/annurev-fluid-011212-140701 Li Lan, Wang Caixia, Grimshaw R. 2015. Observation of internal wave polarity conversion generated by a rising tide. Geophysical Research Letters, 42(10): 4007–4013, doi: 10.1002/2015GL063870 Li Qiang, Farmer D M. 2011. The generation and evolution of nonlinear internal waves in the deep basin of the South China Sea. Journal of Physical Oceanography, 41(7): 1345–1363, doi: 10.1175/2011JPO4587.1 Lien R C, Henyey F, Ma B, et al. 2014. Large-amplitude internal solitary waves observed in the northern South China Sea: properties and energetics. Journal of Physical Oceanography, 44(4): 1095–1115, doi: 10.1175/JPO-D-13-088.1 Liu A K, Chang Y S, Hsu M K, et al. 1998. Evolution of nonlinear internal waves in the East and South China Seas. Journal of Geophysical Research: Oceans, 103(C4): 7995–8008, doi: 10.1029/97JC01918 Ma Xiaochuan, Yan Jun, Hou Yijun, et al. 2016. Footprints of obliquely incident internal solitary waves and internal tides near the shelf break in the northern South China Sea. Journal of Geophysical Research: Oceans, 121(12): 8706–8719, doi: 10.1002/2016JC012009 Masunaga E, Arthur R S, Fringer O B, et al. 2017. Sediment resuspension and the generation of intermediate nepheloid layers by shoaling internal bores. Journal of Marine Systems, 170: 31–41, doi: 10.1016/j.jmarsys.2017.01.017 Maxworthy T. 1979. A note on the internal solitary waves produced by tidal flow over a three-dimensional ridge. Journal of Geophysical Research: Oceans, 84(C1): 338–346, doi: 10.1029/JC084iC01p00338 Miles J W. 1961. On the stability of heterogeneous shear flows. Journal of Fluid Mechanics, 10(4): 496–508, doi: 10.1017/S0022112061000305 Miramontes E, Jouet G, Thereau E, et al. 2020. The impact of internal waves on upper continental slopes: insights from the Mozambican margin (southwest Indian Ocean). Earth Surface Processes and Landforms, 45(6): 1469–1482, doi: 10.1002/esp.4818 Moum J N, Farmer D M, Smyth W D, et al. 2003. Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf. Journal of Physical Oceanography, 33(10): 2093–2112, doi: 10.1175/1520-0485(2003)033<2093:SAGOTA>2.0.CO;2 Moum J N, Klymak J M, Nash J D, et al. 2007. Energy transport by nonlinear internal waves. Journal of Physical Oceanography, 37(7): 1968–1988, doi: 10.1175/JPO3094.1 Nash J D, Moum J N. 2005. River plumes as a source of large-amplitude internal waves in the coastal ocean. Nature, 437(7057): 400–403, doi: 10.1038/nature03936 New A L. 1988. Internal tidal mixing in the Bay of Biscay. Deep-Sea Research Part A. Oceanographic Research Papers, 35(5): 691–709 Orr M H, Mignerey P C. 2003. Nonlinear internal waves in the South China Sea: Observation of the conversion of depression internal waves to elevation internal waves. Journal of Geophysical Research: Oceans, 108(C3): 3064 Ouchi K, Yoshida T. 2023. On the interpretation of synthetic aperture radar images of oceanic phenomena: past and present. Remote Sensing, 15(5): 1329, doi: 10.3390/rs15051329 Puig P, Palanques A, Guillén J, et al. 2004. Role of internal waves in the generation of nepheloid layers on the northwestern Alboran slope: implications for continental margin shaping. Journal of Geophysical Research: Oceans, 109(C9): C09011 Qian Hongbao, Huang Xiaodong, Tian Jiwei, et al. 2015. Shoaling of the internal solitary waves over the continental shelf of the northern South China Sea. Acta Oceanologica Sinica, 34(9): 35–42, doi: 10.1007/s13131-015-0734-4 Quaresma L S, Vitorino J, Oliveira A, et al. 2007. Evidence of sediment resuspension by nonlinear internal waves on the western Portuguese mid-shelf. Marine Geology, 246(2–4): 123–143, doi: 10.1016/j.margeo.2007.04.019 Ramp S R, Tang T Y, Duda T F, et al. 2004. Internal solitons in the northeastern South China Sea. Part I: Sources and deep water propagation. IEEE Journal of Oceanic Engineering, 29(4): 1157–1181, doi: 10.1109/JOE.2004.840839 Reeder D B, Ma B B, Yang Y J. 2011. Very large subaqueous sand dunes on the upper continental slope in the South China Sea generated by episodic, shoaling deep-water internal solitary waves. Marine Geology, 279(1–4): 12–18, doi: 10.1016/j.margeo.2010.10.009 Ribó M, Puig P, Muñoz A, et al. 2016. Morphobathymetric analysis of the large fine-grained sediment waves over the Gulf of Valencia continental slope (NW Mediterranean). Geomorphology, 253: 22–37, doi: 10.1016/j.geomorph.2015.09.027 Richards C, Bourgault D, Galbraith P S, et al. 2013. Measurements of shoaling internal waves and turbulence in an estuary. Journal of Geophysical Research: Oceans, 118(1): 273–286, doi: 10.1029/2012JC008154 Rivera-Rosario G, Diamessis P J, Lien R C, et al. 2020. Formation of recirculating cores in convectively breaking internal solitary waves of depression shoaling over gentle slopes in the South China Sea. Journal of Physical Oceanography, 50(5): 1137–1157, doi: 10.1175/JPO-D-19-0036.1 Scotti A, Pineda J. 2004. Observation of very large and steep internal waves of elevation near the Massachusetts coast. Geophysical Research Letters, 31(22): L22307 Stastna M, Lamb K G. 2008. Sediment resuspension mechanisms associated with internal waves in coastal waters. Journal of Geophysical Research: Oceans, 113(C10): C10016 St Laurent L, Simmons H, Tang T Y, et al. 2011. Turbulent properties of internal waves in the South China Sea. Oceanography, 24(4): 78–87, doi: 10.5670/oceanog.2011.96 Tian Zhuangcai, Jia Yonggang, Chen Jiangxin, et al. 2021. Internal solitary waves induced deep-water nepheloid layers and seafloor geomorphic changes on the continental slope of the northern South China Sea. Physics of Fluids, 33(5): 053312, doi: 10.1063/5.0045124 Tian Zhuangcai, Jia Yonggang, Zhang Shaotong, et al. 2019. Bottom and intermediate nepheloid layer induced by shoaling internal solitary waves: impacts of the angle of the wave group velocity vector and slope gradients. Journal of Geophysical Research: Oceans, 124(8): 5686–5699, doi: 10.1029/2018JC014721 Villamaña M, Mouriño-Carballido B, Marañón E, et al. 2017. Role of internal waves on mixing, nutrient supply and phytoplankton community structure during spring and neap tides in the upwelling ecosystem of Ría de Vigo (NW Iberian Peninsula). Limnology and Oceanography, 62(3): 1014–1030, doi: 10.1002/lno.10482 Whitwell C A, Jones N L, Ivey G N, et al. 2024. Ocean mixing in a shelf sea driven by energetic internal waves. Journal of Geophysical Research: Oceans, 129(2): e2023JC019704, doi: 10.1029/2023JC019704 Yang Y J, Fang Y C, Chang M H, et al. 2009. Observations of second baroclinic mode internal solitary waves on the continental slope of the northern South China Sea. Journal of Geophysical Research: Oceans, 114(C10): C10003, doi: 10.1029/2009JC005318 Yang Y J, Fang Y C, Tang T Y, et al. 2010. Convex and concave types of second baroclinic mode internal solitary waves. Nonlinear Processes in Geophysics, 17(6): 605–614, doi: 10.5194/npg-17-605-2010 Yang Y J, Tang T Y, Chang M H, et al. 2004. Solitons northeast of Tung-Sha Island during the ASIAEX pilot studies. IEEE Journal of Oceanic Engineering, 29(4): 1182–1199, doi: 10.1109/JOE.2004.841424 Zhang Shuang, Alford M H. 2015. Instabilities in nonlinear internal waves on the Washington continental shelf. Journal of Geophysical Research: Oceans, 120(7): 5272–5283, doi: 10.1002/2014JC010638 Zhang Xiaojiang, Huang Xiaodong, Zhang Zhiwei, et al. 2018. Polarity variations of internal solitary waves over the continental shelf of the northern South China Sea: Impacts of seasonal stratification, mesoscale eddies, and internal tides. Journal of Physical Oceanography, 48(6): 1349–1365, doi: 10.1175/JPO-D-17-0069.1 Zhao Zhongxiang, Klemas V, Zheng Quanan, et al. 2004. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea. Geophysical Research Letters, 31(6): L06302 Zheng Hua, Zhu Xiaohua, Wang Min, et al. 2024. The largest CPIES array in the marginal sea: abundant dynamics in the northeast South China Sea. Acta Oceanologica Sinica, 43(1): 135–137, doi: 10.1007/s13131-024-2293-z Zulberti A, Jones N L, Ivey G N. 2020. Observations of enhanced sediment transport by nonlinear internal waves. Geophysical Research Letters, 47(19): e2020GL088499, doi: 10.1029/2020GL088499 -

 点击查看大图
点击查看大图
计量
- 文章访问数: 169
- HTML全文浏览量: 62
- 被引次数: 0



 DownLoad:
DownLoad:
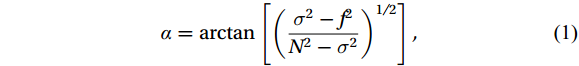

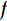

 下载:
下载: