Forecasting of surface current velocities using ensemble machine learning algorithms for the Guangdong−Hong Kong−Macao Greater Bay area based on the high frequency radar data
-
Abstract: Forecasting of ocean currents is critical for both marine meteorological research and ocean engineering and construction. Timely and accurate forecasting of coastal current velocities offers a scientific foundation and decision support for multiple practices such as search and rescue, disaster avoidance and remediation, and offshore construction. This research established a framework to generate short-term surface current forecasts based on ensemble machine learning trained on high frequency radar observation. Results indicate that an ensemble algorithm that used random forests to filter forecasting features by weighting them, and then used the AdaBoost method to forecast can significantly reduce the model training time, while ensuring the model forecasting effectiveness, with great economic benefits. Model accuracy is a function of surface current variability and the forecasting horizon. In order to improve the forecasting capability and accuracy of the model, the model structure of the ensemble algorithm was optimized, and the random forest algorithm was used to dynamically select model features. The results show that the error variation of the optimized surface current forecasting model has a more regular error variation, and the importance of the features varies with the forecasting time-step. At ten-step ahead forecasting horizon the model reported root mean square error, mean absolute error, and correlation coefficient by 2.84 cm/s, 2.02 cm/s, and 0.96, respectively. The model error is affected by factors such as topography, boundaries, and geometric accuracy of the observation system. This paper demonstrates the potential of ensemble-based machine learning algorithm to improve forecasting of ocean currents.
-
Key words:
- forecasting /
- surface currents /
- ensemble machine learning /
- high frequency radar /
- random forest /
- AdaBoost
-
1. Introduction
Offshore development is empowered by improved understanding of marine environment and advancement of marine technologies. Multiple installations have been constructed in the ocean including offshore airports, platforms and island construction (Kim et al., 2021). Stability of marine engineering and structures under the action of ocean currents is a dynamic response process. Marine structures need to withstand complex and harsh marine loads, including ocean currents, waves, and winds. Timely and accurate forecasting of ocean currents can enhance the safety of marine structures, guide ocean activities, and can provide support for disaster prevention and mitigation system. Forecasts can also inform site selection, environmental impact assessment and cost-benefit analysis for multiple projects. For example, ocean current forecasting provide guidance for the design, placement, configuration, and installation of ocean turbines to maximize production and ensure the stability and safety of the turbine (Dinh and McKeogh, 2019).
The maturation of advanced remote sensing systems such as high frequency radars (HFRs) and satellites make it be feasible to obtain real-time information of ocean parameters over a wide range at fine temporal and spatial resolution (Klemas, 2011). HFRs are cost-efficient tools to sample large swathes of the ocean over an extended period. HFRs can measure the speed and direction of surface currents, wind speed, wind direction, wave height, wave period, and wave direction. It has demonstrated robust performance in a number of operational situations such as coastal monitoring, port operations, and search and rescue (Basañez and Pérez-Muñuzuri, 2021).
Forecasting models are critical to numerous industry and societal applications such as shipping, agriculture, construction, and government (Immas et al., 2021). Ocean circulation is a nonlinear dynamical process that is influenced by a combination of factors and interactions among them. In previous studies, numerical models and machine learning algorithms had been applied to develop forecasting models for marine parameters. While numerical models are a powerful forecasting tool, the characteristics are physical principles-based, useful for long-term prediction and suitable for global or regional scales. They often require deep expertise to parametrize and configure the model as well as immense computational power to generate forecasts. Further, model accuracy and uncertainty require a deep analysis of grid discretization, boundary condition specification, and the specific topographical and bathymetric properties of the area.
Machine learning has demonstrated impressive performance across a variety of tasks in recent years. Ingesting information from disparate observation sources, reanalysis, and forecast data has enabled high predictive skills across complex environmental applications. Machine learning models can identify and learn nonlinear relationships and complex patterns in data, which is very useful for understanding and predicting complex ocean current dynamics processes (Wang et al., 2023a). Additionally, machine learning models can adapt to different ocean current characteristics and variations by adjusting network structure and parameters, and have good flexibility and adaptability. As the volumes of earth system data continue to increase, machine learning is becoming a key tool for many scientists.
Machine learning has demonstrated success in ocean applications across data mining, improved forecasting, event detection, and decision support (Mitchell, 1999). Ren and Hartnett (2017b) used a decision tree algorithm to forecast the surface currents at a marine renewable energy test site in the Galway Bay, Ireland. Reported correlation coefficient between observations and model outputs exceeded 0.89. Ren et al. (2018) used an error back propagation artificial neural network (BP-ANN) algorithm to build a model to forecast surface current velocities. Ingesting tidal information, wind data, and historical radar measurements as input variables, correlation coefficients between model and observations exceeded 0.9. Aydoğan et al. (2010) applied the feedforward back propagation artificial neural network (FFBP-ANN) to build a forecasting model, of current profiles, which reported root mean square error of 16 cm/s. Bradbury and Conley (2021) used a recurrent neural network model trained with a Bayesian regularization algorithm to forecast subsurface currents through using HFR data as inputs. The forecasting accuracy was evaluated as decision factor by 0.98, mean absolute error by 5 cm/s and Nash-Sutcliffe efficiency by 0.98. Therefore, several previous studies had incorporated machine learning methods into forecasting of surface currents. Quantitative statistical assessments indicate that these models generate satisfactory results.
Machine learning methods can extract non-linear information from data and learn the dynamics directly without being programmed. Artificial neural network (ANN) algorithms have been widely applied, but few studies have used ensemble learning algorithms for ocean currents forecasting. Unlike ANN, ensemble learning algorithms do not seek to get a single optimal learner, but combine a number of weak learners to improve overall performance (Yang, 2017). This has been shown to outperform a best individual performing model across a wide variety of tasks (Sagi and Rokach, 2018). Further, they are generally more interpretable than neural network-based methods.
Bagging and boosting are two important techniques of ensemble learning methods. Bagging creates a weak learner by perturbing the sample set and forecasting parameters. Random forest (RF) is a prominent example. Boosting works by making each newly constructed weak learner pay more attention to the samples with large deviation from the previous regression by changing the weight assignment. AdaBoost, short for Adaptive Boosting, is a popular example of boosting. It iteratively trains the weak predictors by adjusting the weights of data points further from the mean, emphasizing their importance in subsequent iterations. The final forecasting is obtained by weighing the forecasting of each weak predictor according to its performance.
Based on the strong forecasting skill of ensemble algorithms, this study combined RF and AdaBoost algorithm to establish a machine learning framework for short-term forecasting of surface current velocities in coastal areas of the Guangdong−Hong Kong−Macao Greater Bay area (GBA). The objectives are to provide a scientific basis and reference tool for channel forecasting, disaster prevention and mitigation, coastal rescue and marine engineering construction in this area.
The rest of the paper is structures as follows. Section 2 briefly describes methodologies including study area, datasets, and machine learning algorithms. Section 3 presents the main results, followed by discussion in Section 4. The main conclusions are presented in Section 5.
2. Methodologies
2.1 Study area
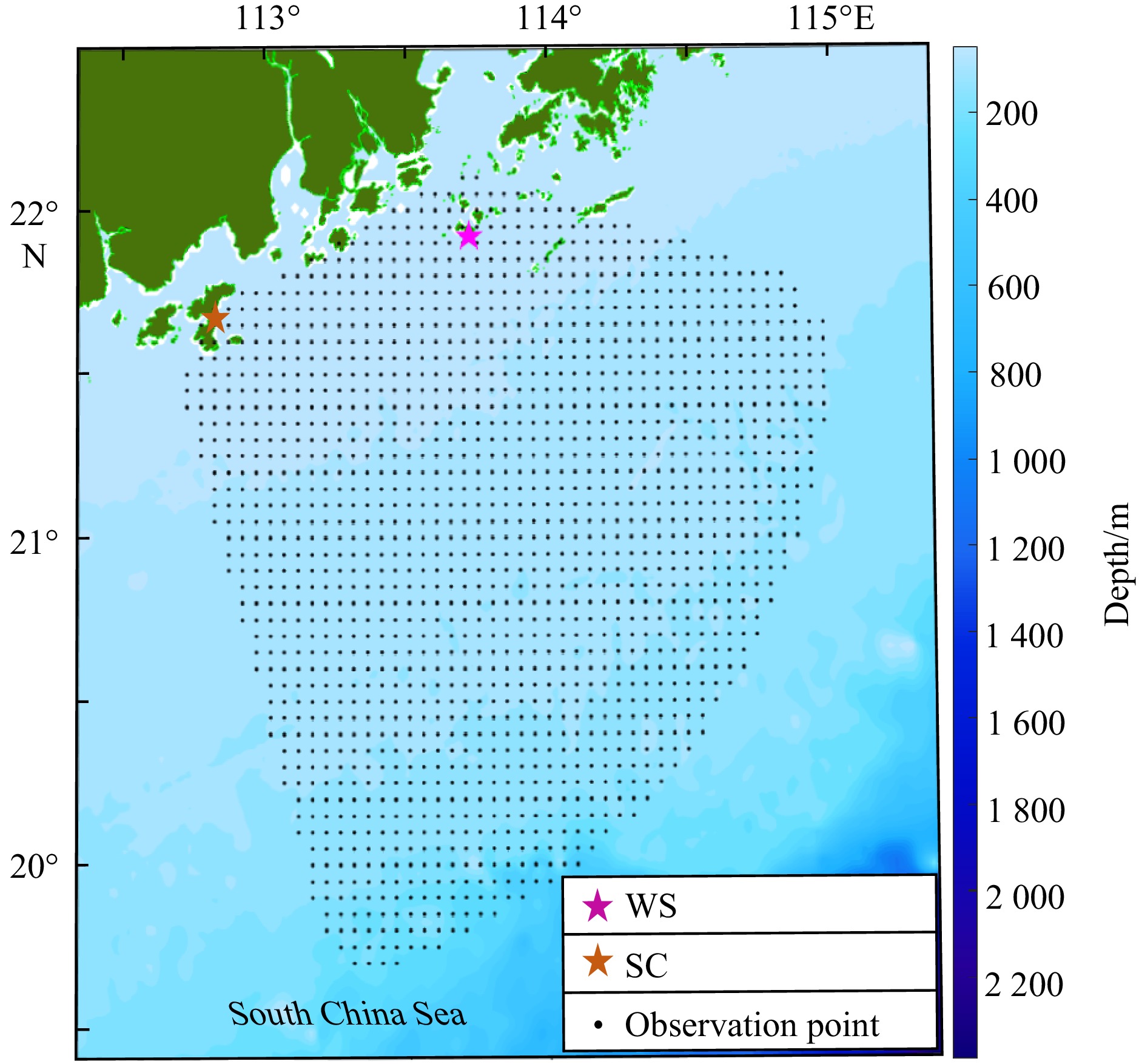
The study area (GBA) is located in the South China Sea and connected to the Lingdingyang in the north (Fig. 1). The coastlines are characterized by numerous capes and bays, serpentine coastlines and well-developed estuaries and bays formed by tectonic activity (Jishun, 1991). Natural processes such as tides, wind, land-runoff, bathymetry, topographical steering, and other factors, combined with anthropogenic activities, such as shoal reclamation and waterway dredging, have created a complex and dynamic hydrodynamic system in coastal parts of GBA (Wei et al., 2021).
Additionally, the study area is strongly influenced by monsoons. Southwest winds dominates in the summer, with maximum wind speed of 7 m/s, while Northeast winds dominate in winter, with an averaged wind speed of 8–10 m/s (Lin et al., 2003). Monsoon events are a dominant forcing factor for the upper ocean circulation in this area. Strong wind stress or curls directly drive local strong ocean currents, basin-scale, and mesoscale circulations (Liu et al., 2008). Coastal ocean currents are greatly influenced by runoff from land sources, while several rivers run into the bay creating complex hydrodynamic and environmental processes (Yang et al., 2021). Coastal currents flow westward in the west parts of the Zhujiang River (Pearl River) Estuary all year round. Part of the westward Guangdong coastal currents in summer form the northern flank of the cyclonic circulation, and partial currents enter the Beibu Gulf through the Qiongzhou Strait (Wang et al., 2021). Tidal amplitude and variation in tidal properties along the coast of the GBA are mainly affected by topographic changes (Fang et al., 2015). Tidal currents rotate in a counterclockwise direction. Amplitudes gradually increase from the northern South China Sea to the coast of Guangdong as the water depth becomes shallower (Ye and Robinson, 1983). The dominant tidal constituents are M2, K1, O1, and S2 creating irregular semi-diurnal tidal currents (Wang and Rainbow, 2020). This area is dominated by baroclinic diurnal tides with phase changes in both vertical and horizontal directions (Li et al., 2014). Lack of real-time, large-scale, and refined continuous observations hinder the understanding of regional ocean physical processes. This is the first time that the HFR system had been deployed and applied in this area, which enables continuous observation of the surface current fields across the sub-tidal cycle, providing a possibility of progress for unresolved and unexplained physical processes. It is important that the rich observation dataset is combined with a flexible forecasting framework to enable forecasting and address data gaps.
2.2 Datasets
2.2.1 Wind data
The wind speed data used in this study were obtained from the European Centre for Medium-Range Weather Forecasts (ECMWF) at a spatial and temporal resolution of 0.25° × 0.25° and 1 h, respectively.
2.2.2 HFR data
Conventional acquisitions of ocean currents are through numerical simulation and in-situ sensors, with in-situ data typically being more precise. The HFR observation data used in this study provide a scalable and efficient means to analyze the spatial and temporal characteristics of ocean currents. The working principles of the HFR are based on the Doppler effect to measure the motion of ocean surface currents. Radio waves emitted from the station propagate over the ocean waves. When waves encounter surface currents or surface waves, they experience a frequency shift due to the Doppler effect. The frequency shift is proportional to the velocity of the ocean currents (Yin et al., 2018). The received echo returns are processed using Doppler analysis techniques (Barrick et al., 1974). A single radar station can only provide radial ocean currents. Radial surface currents obtained by two or more HFR stations are synthesized to obtain total surface current fields (Mantovani et al., 2020). Due to significant advantages including large range, high precision and all-weather of HFR observations, HFR systems had been deployed in coastal area around the world, such as the western coast of Ireland (Ren and Hartnett, 2017a), the Taiwan coasts (Chen et al., 2021), the south-western Australian Coast (Cosoli et al., 2020) and the eastern Tsugaru Strait, Japan (Wang et al., 2023b).
The ocean state measuring and analyzing radar (OSMAR) system developed by Hubei Zhongnan Pengli Marine Exploration System Engineering Co., Ltd have been deployed in the study area. Two radar sites are located on the Shangchuan Island and Wanshan Island (Fig. 1), respectively. Distance between the two stations is approximately 98 km. The farthest range of the radar is approximately 200 km and the total coverage area is nearly 40 000 km2. HFR stations suffer from the same geometric dilution of precision challenges as global positioning system. In short, locations where signals from both stations intersect at right angles report highest accuracy with gradual degradation as the angle approaches zero. In our study site, intersection area of the radar with the 30° opening angle is the core area of radar observation, with a total area approximately 666 km2. The intersection area with the 60° opening angle is a high-precision area with a total area approximately 4 137 km2. Intersection area of 120° opening angle of Wanshan Island Station and 87° opening angle of Shangchuan Island Station is approximately 11 655 km2 in total. The specific geographical location of the radar stations and its observation area are shown in Fig. 1.
HFR systems sample the surface of the ocean to a depth of approximately 1.5 m. The study covers a period from 00:00 April 1, 2021 to 23:00 June 30, 2021 (UTC+8). Temporal resolution was 10 min and the spatial coverage 19.7°–22.1°N, 112.7°–115°E with spatial resolution of 0.05° × 0.05°. Synthesized sea surface current vector fields have 1 564 observational points in total (Fig. 1). The observation points are located in the coastal waters of the GBA with a water depth 0–200 m. The isobaths in the study area are basically parallel to coastlines and the water depth gradually becomes deeper with the increase of offshore distance. The study first preprocessed the HFR data by removing outliers and filling in missing values using cubic spline interpolation. Observations with data acquisition rates greater than 90% (high-density points) were used for surface current characterization, and the pre-processed data set was used for predictive analysis. Although outliers and gaps due to equipment malfunctions, weather conditions, clutter interference etc. exist in HFR observation data, it is still one of the powerful means to obtain marine parameters including ocean currents, waves and winds over a large domain in coastal areas. Thus, it has been becoming an important data source for a variety of studies and applications.
2.3 Algorithms
2.3.1 Random forest algorithm
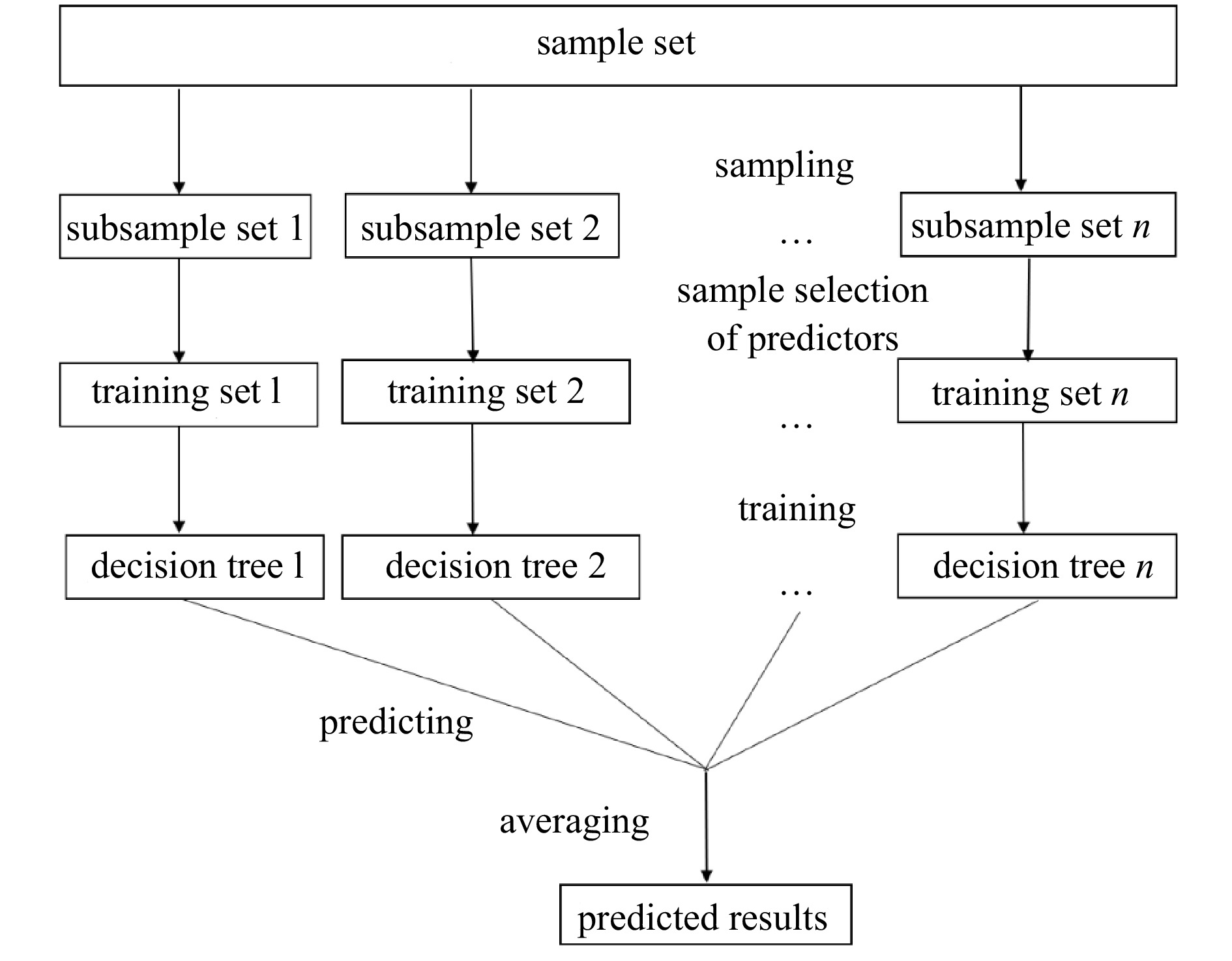
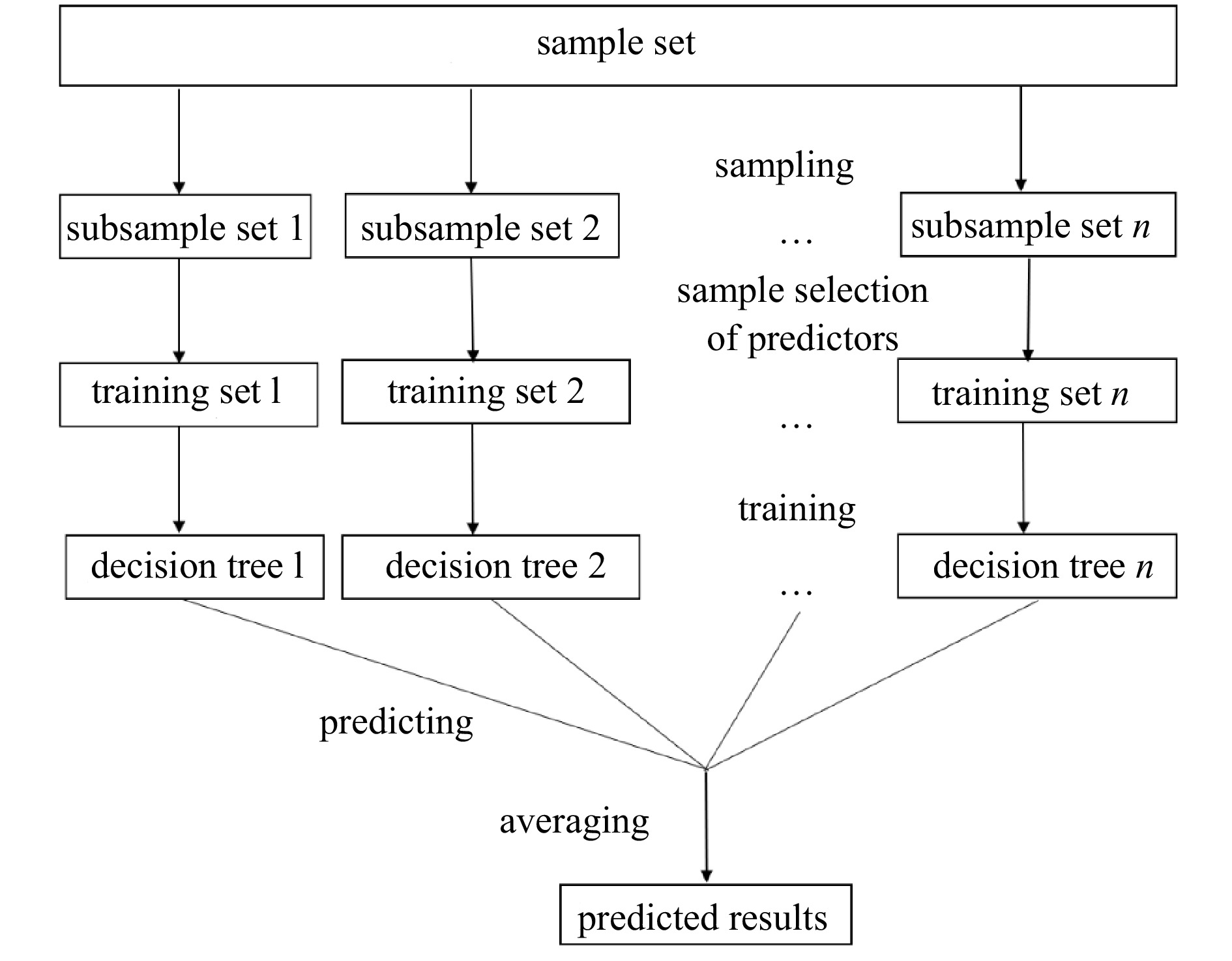
Random forest algorithm is highly flexible, ensemble machine learning method proposed by Breiman (2001). Its algorithm generalization process is shown in Fig. 2. Firstly, multiple samples are drawn from the original samples using the bootstrap resampling method, and then m features are selected by random sampling from M forecasting features, and a regression tree model is established for each bootstrap sample (Hastie et al., 2009). A “forest” is a combination of forecasts from multiple unrelated decision trees. For the regression, the forecast from each tree is averaged as the final output (Ali et al., 2012). RF is an ensemble of regression trees, which makes it more robust than a single regression tree. The risk of overfitting is avoided by adding uncertainty during construction so that forecasting is not unduly influenced by specific current velocities or candidate forecasting features.
The trees grown based on bootstrap samples are forecasted and aggregated with out-of-bag (OOB) data not used in training. The loss function (mean-square error, MSE) can be used to estimate an error rate for the RF model. Additionally, the RF can evaluate the importance of variables by calculating the averaged information gain of features. Its formula is as follows (Ma et al., 2017):
$$ {\mathrm{VI}}\left( {{X_f}} \right) = \frac{1}{N}\sum\limits_{i \;= \;1}^N {\left( {{\mathrm{errOOB}}'_i - {\mathrm{errOO}}{{\mathrm{B}}_i}} \right)} , $$ (1) where
${\mathrm{VI}}\left( {{X_f}} \right)$ represents the importance of f-th variable${X_f}$ ; N is the number of decision trees in the RF;${\mathrm{errOO}}{{\mathrm{B}}_i}$ is the out-of-bag estimation error of the i-th tree;${\mathrm{errOO}}{{\mathrm{B}}'_i}$ is the out-of-bag estimation error of the i-th tree after adding random noise to${X_f}$ .The larger the change in the out-of-bag errors caused by the noise disturbance have, the larger
$ \mathrm{VI}\left(X_f\right) $ , the more important representative variable${X_f}$ . This property enables RF models to assess which candidate forecasting feature has the greatest impact on forecasting during multivariate forecasting. Relative impact of candidate forecasting features on forecasting can be quantified using MSE, which facilitates the interpretation and analysis of the model. The modeling and calculation of RF in this study were implemented using MATLAB. The number of decision trees N is a hyper-parameter to be defined as part of model training derived from trial calculations. By trial calculation, when the MSE tends to be smooth, N is taken as 500.2.3.2 AdaBoost algorithm
AdaBoost has several advantages, such as being fast, simple and easy to program. AdaBoost is especially appealing since it tends to work well with the default parameters. There are two kinds of weights in the AdaBoost algorithm. One is the weight of the data, and the other is the weight of the weak learner. To make the model pay more attention to data points with large regression errors, each time a new learner is established, the weights assigned to these data points are increased. By assigning the weights of weak learners, a family of strong learners can be assembled. The specific steps of the AdaBoost are as follows (Wen et al., 2015).
Step (1): The training set is divided from the data set and can be expressed as
$$ T = \left\{ {\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right), \cdots ,\left( {{x_n},{y_n}} \right)} \right\}, $$ (2) where
${x_n}$ is the feature input set;${y_n}$ is the corresponding output set.Step (2): Initializing the weight distribution
${D_1}$ of the training samples as$$ {D_1} = \left( {{w_1},{w_2}, \cdots ,{w_{{n}}}} \right) , $$ (3) where
${w_n}$ is the weight representing the n-th group of data.Step (3): Calculating the learner weight parameter ag as follows:
$$ a_{g}=\frac{1}{2}\;\text{ln}\left(\frac{1-\displaystyle\sum_{ }^{ }w_n}{\displaystyle\sum_{ }^{ }w_n}\right). $$ (4) Step (4): Using the sample data set with the initial weight set D1 to train the base regression learner G1, and to calculate the absolute error
${e_n}$ for each set of samples. If${e_n}$ > C (C can be set according to the actual situation), multiply the corresponding weight${w_n}$ by ɑ, otherwise multiply the weight${w_n}$ by β. After redistributing the weights corresponding to each group of samples, a new weight set is obtained and normalized to D2. The learner weight parameter a2 is obtained at the same time. Weight set D2 is used to train the regression learner G2. The m weak learners G1–Gm and their corresponding weights a1–am are obtained through the process of continuously cyclically assigning weights and training new learners.Step (5): Normalizing the learner weights a1–am as follows:
$$ {a _g} = \frac{{{a _g}}}{{\displaystyle\sum\limits_{g = 1}^m {{a_g}} }} . $$ (5) Step (6): Assembling the final strong ensemble learner f(x) as follows:
$$ f\left( x \right) = \sum\limits_{g \;=\; 1}^m {{a _g}{G_g} \left( x \right)} . $$ (6) The weak learner integrated in this study based on the AdaBoost algorithm is a randomly generated BP-ANN model. The number of ensembles m is 30. There is no need for complex parameter tuning of artificial neural networks. The AdaBoost algorithm adopts the strategy that when the absolute error of the forecasting results is greater than 5 cm/s, the initial weight of the “difficult” tuple is given a multiple of ɑ = 1.10 through trial computation; when the absolute error is less than or equal to 5 cm/s, the initial weight of the tuple is given a multiple of β = 0.90 (Sun et al., 2022). These model hyper-parameters were selected based on grid-search approach. Weak learners with different advantages can be integrated through continuous accumulation and adjustment of weight distribution.
2.4 Assessment skills
To evaluate model accuracy, the correlation coefficient (R), the mean absolute error (MAE) and the root mean square error (RMSE) were used as evaluation criteria. They are calculated as follows (Han et al., 2019):
$$ R = \frac{{\displaystyle\sum {\left( {x - \overline x} \right)} \left( {y - \overline y} \right)}}{{\sqrt {\displaystyle\sum {{{\left( {x_i - \overline x} \right)}^2}} } \sqrt {{{\displaystyle\sum {\left( {y_i - \overline y} \right)} }^2}} }} , $$ (7) $$ {\mathrm{MAE}} = \frac{1}{c}\sum\limits_{i \;=\; 1}^c {\left| {\widehat {y_i} - {y^{\left( i \right)}}} \right|} , $$ (8) $$ {\mathrm{RMSE}} = \sqrt {\frac{1}{c}\sum\limits_{i\; =\; 1}^c {{{\left( {\widehat y_i - {y^{\left( i \right)}}} \right)}^2}} } , $$ (9) $$ {\mathrm{MSE}} = \frac{1}{c}\sum\limits_{i\; =\; 1}^c {{{\left( {\widehat y_i - {y^{\left( i \right)}}} \right)}^2}} , $$ (10) where c is the number of samples; y(i) is the measured sea current data of HFR;
$ \widehat y_i $ is the regression value of the model;$\bar x $ and$\bar y $ are the sample means of variable x and y, respectively; x and y are two different dataset.2.5 Pre-processing
2.5.1 Study area pre-processing
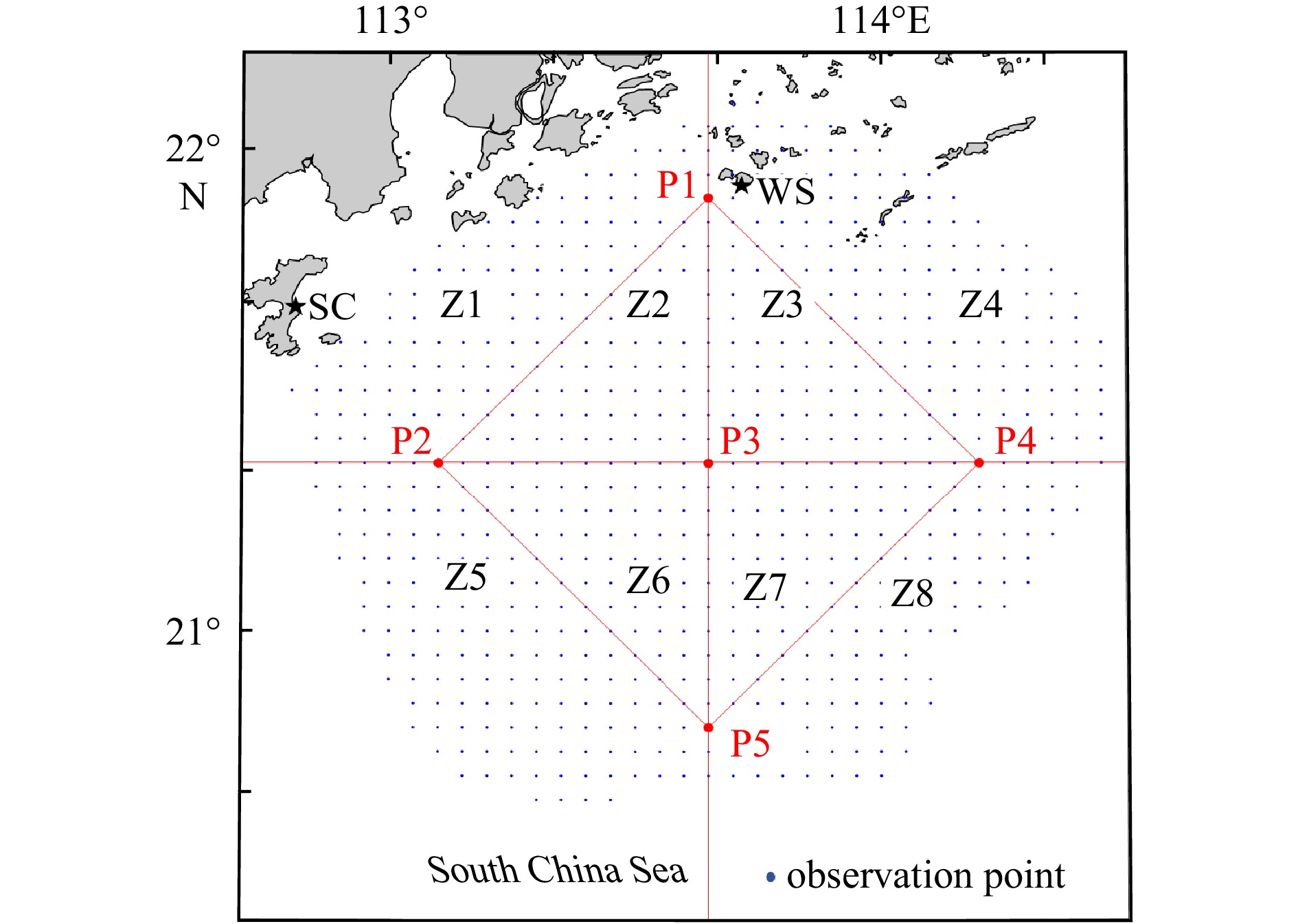
This study extends previous research on time series forecasting at a single location by Ren and Hartnett (2017b). In order to generate forecasting of surface current velocities in space through comprehensively consideration of multiple factors, the study area was regularly divided into eight sub-areas through five benchmark points. In this study, the established single-point ocean current forecasting model was extended to multiple spatial points by selecting representative points of sub-areas in the research area (Fig. 3). Five fixed points were selected, namely P1 (21.90°N, 113.65°E), P2 (21.35°N, 113.10°E), P3 (21.35°N, 113.65°E), P4 (21.35°N, 114.20°E), and P5 (20.80°N, 113.65°E). Since surface current velocities vary in space, in order to make the developed forecasting model be versatile and effective, the five representative points were connected in pairs to divide study area into eight sub-zones (Z1–Z8 in Fig. 3).
2.5.2 Forecasting feature selection
Before modeling training and forecasting, model input variables need to be determined. If all data are used as model inputs, it is not only computationally intensive, but also impacts model accuracy. However, existing feature selection approaches are often heuristic and lacks theoretical basis. Therefore, in this study, the input features were firstly determined by using the sea surface flow characteristics analysis. The study conducted tidal current reconciliation analysis for the five representative points and performed tidal pattern coefficient and shallow water coefficient calculations, the results of which are shown in the Table 1.
Table 1. Statistics of tidal ellipticity, tidal type coefficients and shallow water coefficientsPoint Tidal ellipticity Tidal type
coefficientShallow water
coefficientO1 K1 M2 S2 P1 –0.4 –0.06 –0.22 0.12 1.51 0.32 P2 –0.10 –0.11 –0.02 0.21 1.11 0.20 P3 –0.07 –0.2 –0.02 0.29 1.09 0.20 P4 0.22 –0.34 –0.05 –0.12 1.27 0.19 P5 –0.37 –0.27 –0.31 0.44 1.68 0.24 The tidal types of P1–P5 are all irregular semidiurnal currents. It can be assumed that the tidal type of the whole study area is irregular semidiurnal currents. When considering the influence of tidal currents on the forecasting of surface currents, the M2 divergence is the main influence at most of the representative points, but daily harmonics still occupies an important position that cannot be ignored, especially at the eastern and southern representative points of the study area. The shallow water effect is significant at all five representative points. It can be considered that the shallow water fractional tide effect is significant in the whole study area. Meanwhile, it is natural to expect a decay of signal strength with more recent observations having a stronger influence on forecasting. Hence, a historical sequence of 26 h was selected as features to the model.
The second feature selection approach considered the relationship between residual currents and wind speeds. Previous studies have found significant influence of sea-air coupling on residual circulation dynamics (Cheng and Valle-Levinson, 2009). Table 2 presents the optimal correlation coefficients and lag times between residual current velocities and wind speeds for each representative point.
Table 2. Statistics of the optimal correlation coefficients of surface current componentsPoint Correlation coefficient Lag time/h Zonal component Meridional component Zonal component Meridional component P1 0.75 0.31 12 11 P2 0.78 0.31 12 8 P3 0.79 0.22 11 9 P4 0.68 0.24 9 9 P5 0.55 –0.09 11 9 As presented in Table 2, this study considers 20-h lagged wind speed data based on the above analysis and additional tolerance for uncertainty. The current velocities at the five representative points are significantly influenced by the wind, and the situation varies at different points reflecting complex wind-sea catch dynamics.
2.5.3 Forecasting model set-up
Single time-step of the surface current forecasting model is 10 min (
$ \mathrm{\Delta }t=10\;\mathrm{m}\mathrm{i}\mathrm{n} $ ), and Tg represents the time after g time-steps$\Delta t$ . The training dataset is the first 85% of the dataset in chronological order; the test dataset is the last 15%. Inputs are the features of surface currents and wind speeds (156 historical sea surface current data reflecting 26 h of data at 10 min intervals and 20 wind speed data pairs). Output values are the sea surface current velocities at the moment of Ti. Details of the model settings bare as follows (Table 3). (1) Baseline model: all forecasting features were used as input features to build the AdaBoost forecasting models. (2) Application model: the information gain rate of each candidate forecasting feature was analyzed by RF algorithm to quantitatively determine the importance of the variables. Variable importance was ranked in descending order and accumulated one by one. Features whose total variable importance accumulates over 95% were retained and used as new features for the input of the AdaBoost forecasting model. (3) Rolling model: for multiple time-steps, the application model in Step (2) was used, and the input features of each time-step were the features whose importance accumulates over 95% at the first time-step; reconstruction model: for multiple time-steps, the model structure was optimized on the basis of Step (3), and the importance of the variables at each time-step was analyzed to dynamically select the features.Table 3. Forecasting model set-upModel Algorithm Feature Feature selection Forecasting model Baseline model \ AdaBoost total observation data Application model random forest AdaBoost observation data whose total variable importance accumulates over 95% Rolling model random forest AdaBoost observation data whose importance accumulates over 95% at the first time-step Reconstruction model random forest AdaBoost observation data whose importance accumulates over 95% at each time-step Note: \ denotes no feature selection. 3. Results
3.1 Forecasting of surface current velocities at single time-step
3.1.1 Forecasting of surface current velocities at single time-step of P1
Historical surface current data from 1 time-step to 156 time-steps (i.e., 26 h) before the forecasting time T are recorded as CS1–CS156. Historical wind data from 1 step to 20 steps (i.e., 20 h) before the forecasting time T are recorded as WS1–WS20. In order to explore the confidence of the forecasting model, the forecasting model for the single time-step sea surface current zonal component at P1 was firstly constructed using all the features. Results indicate that the forecasting has a good agreement with the HFR observations. Correlation coefficient is 0.999 5, RMSE is 0.96 cm/s and the averaged absolute error is 0.55 cm/s. The baseline model meets the needs of engineering in terms of forecasting and gap filling. However, in practical applications, due to the large number of calculation points and the huge amount of data, the input structure of the transition model is further optimized to reduce the calculation cost.
Random Forest is an ensemble learning method that, in terms of feature parameter selection, calculates the average decrease in impurity or accuracy of features across all decision trees to obtain the importance score of features. Based on quantitative indicators, it guides feature selection without being affected by empirical biases (Mao et al., 2022). Based on the RF algorithm, the variable importance of each forecasting feature was quantitatively evaluated. Since there is a large order of magnitude difference between the impact of historical wind data and historical surface currents when the weights of the zonal component forecasting features for a single time-step at P1 were counted, only representative features of relatively high importance are shown in Fig. 4. Results indicate that there are differences in the contribution of historical surface current data to forecasting at T with a pronounced temporal decay. It indicates that more recent observations dominate forecasting.
In order to improve the computational efficiency of the model, features accounting for more than 95% of the total variable importance were used as new features for further simplification. For the baseline model of single-step surface current zonal component forecasting at P1, there are eight simplified forecasting features, CS1–CS8. Forecasting results of the application model obtained by simplifying the baseline model based on the RF algorithm have a good agreement with the HFR observations. The correlation coefficient is 0.99, the RMSE is 1.04 cm/s and the average absolute error is 0.58 cm/s. It indicates that the accuracy of the application model was only slightly lower than that of the baseline model. The training time of the transition model is 80.43 s, and the training time of the application model is only 7.22 s. The calculation time is greatly reduced, and the consumption time of the application model is only 8.97% of the baseline model. Therefore, the application model was used to promote forecasting of surface currents in space.
Single time-step forecasting baseline models and application models for both surface current zonal and meridional components were established at the representative points P1–P5. Statistics of model evaluation for training set are presented in Table 4. High correlation coefficients (greater than 0.98) indicates that the developed models can generate satisfactory forecasting of both velocity components at these points for single time-step ahead. Values of MAE are less 2.2 cm/s for both velocity components at five points. Except for zonal component at representative point P5, values of RMSE are less than 2.7 cm/s. Results indicate that in comparison with the baseline model, forecasting accuracy of the application models only drops slightly at significantly reduced computational expense.
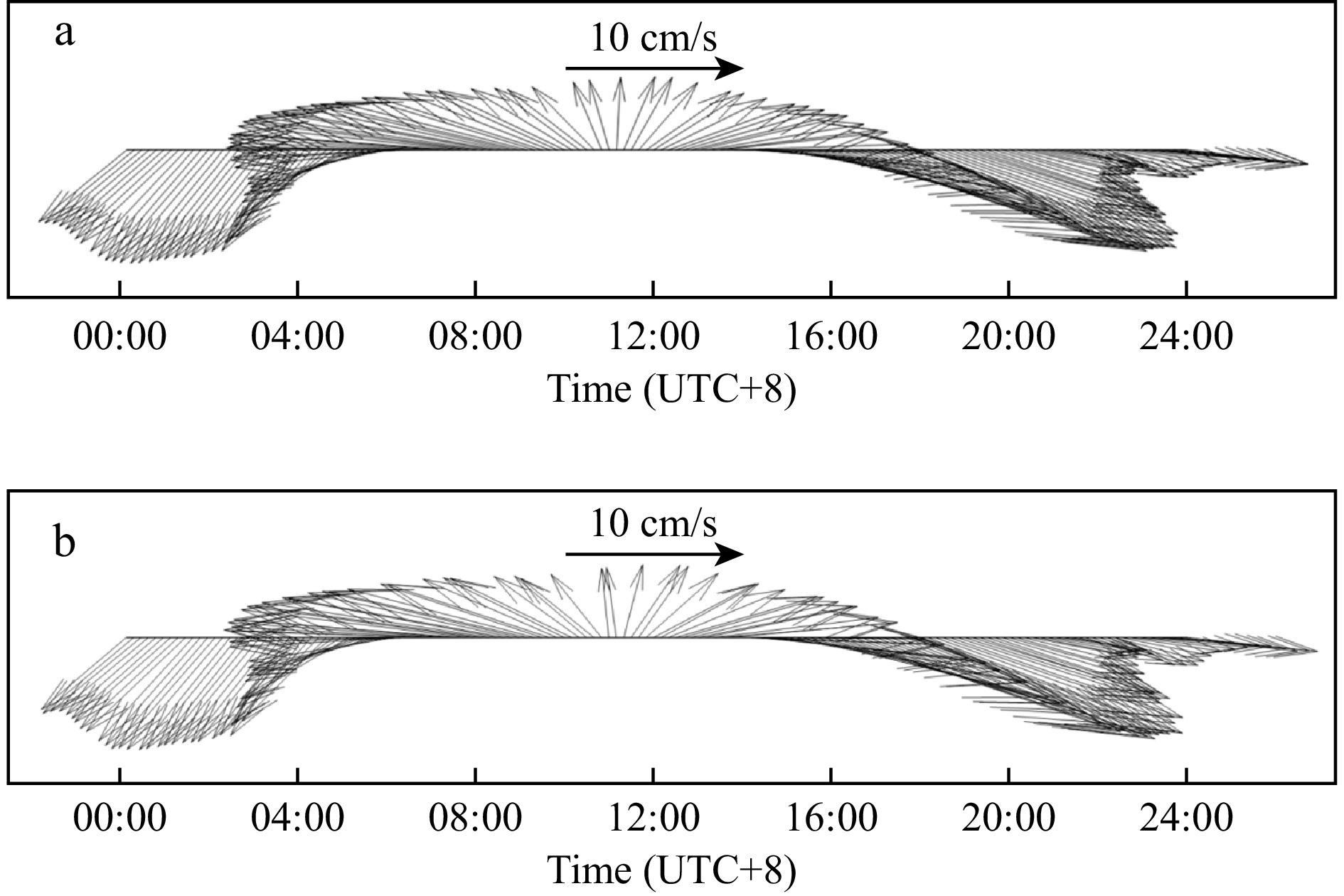
Table 4. Assessment statistics of single time-step forecasting (training dataset)Point Zonal component of surface velocity assessment statistic Meridional component of surface velocity assessment statistic Feature number RMSE/(cm·s–1) R MAE/(cm·s–1) Feature number RMSE/(cm·s–1) R MAE/(cm·s–1) P1 176 0.96 1.00 0.55 176 0.87 1.00 0.40 8 1.04 1.00 0.58 8 0.94 1.00 0.58 P2 176 1.46 1.00 0.82 176 1.31 0.99 0.73 9 1.56 1.00 0.85 8 1.42 0.99 0.76 P3 176 0.96 1.00 0.52 176 1.06 1.00 0.45 8 1.04 1.00 0.55 8 1.14 0.99 0.46 P4 176 2.41 0.99 1.29 176 2.52 0.98 1.35 9 2.60 0.99 1.36 36 2.68 0.98 1.36 P5 176 3.55 0.98 2.11 176 1.69 0.99 0.81 13 4.06 0.98 2.16 13 1.80 0.99 0.85 Table 5 presents statistics of model evaluation for test dataset. It indicates that the forecasting model of surface current zonal component at point P1 outperform others, RMSE is 0.95 cm/s, correlation coefficient is close to 1, and MAE value is 0.62 cm/s. Vectors of surface currents at point P1 over one day are shown in Fig. 5. It demonstrates that the model captures the evolution of the periodic tidal trend, and the forecasting of flood and ebb current time. Accuracy of the forecasting model for the zonal component of surface current is higher than that of the meridional component. Correlation coefficients are greater than 0.94 for both velocity components at these analysis points, which indicates that there are good agreement between forecasting and observations. Values of RMSE are less than 4 cm/s, except for point P4. Values of MAE are less than 2 cm/s, except for meridional component at P4 by 3.29 cm/s.
Table 5. Assessment statistics of single time-step forecasting (test dataset)Point Zonal component of surface velocity assessment statistic Meridional component of surface velocity assessment statistic Feature number RMSE/(cm·s–1) R MAE/(cm·s–1) Feature number RMSE/(cm·s–1) R MAE/(cm·s–1) P1 8 0.95 1.00 0.62 8 1.66 0.99 0.67 P2 9 2.41 0.99 1.00 8 2.05 0.98 0.85 P3 8 1.55 1.00 0.71 8 3.68 0.97 1.04 P4 9 5.02 0.98 1.62 36 9.36 0.94 3.29 P5 13 2.97 0.98 1.75 10 1.90 0.99 0.84 3.1.2 Forecasting of surface current fields at single time-step
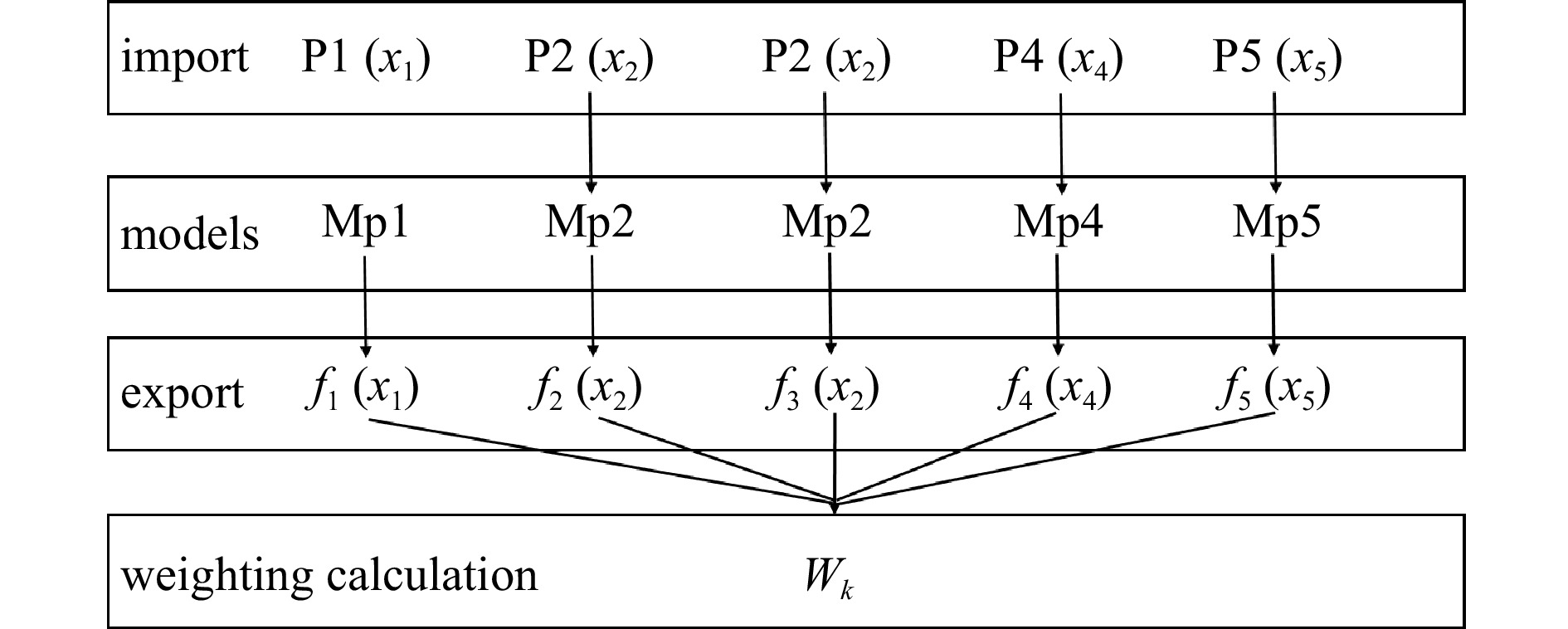
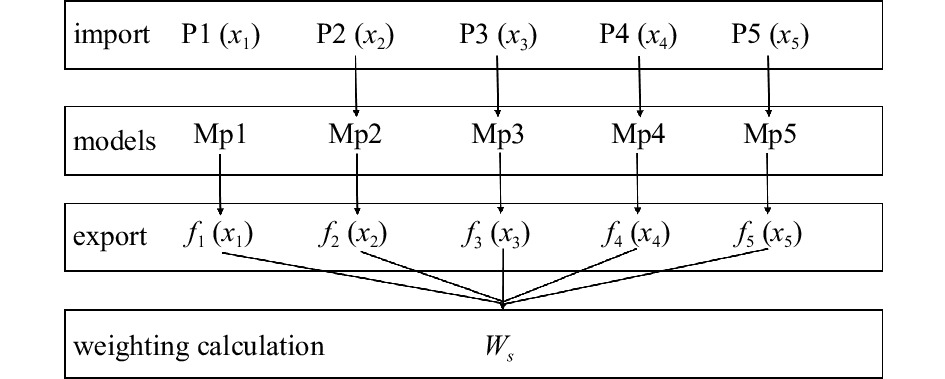
Many previous studies focus on forecasting at a single location. However, practical applications require surface current fields in space. This section details extension of forecasting models to the entire study area. Application models for points P1–P5 were denoted as Mp1–Mp5, respectively. These were extended to spatial maps using an inverse distance weighted averaging. The widely used inverse distance weighting method is a common form of spatial interpolation based on the similarity principle (Johnston et al., 2001; Vavatsikos et al., 2022). The values of the interpolated points are jointly influenced by the values of the sample points and their weights within the spatial points. The observation points on the regional line segment only consider two representative endpoints of the line segment.
Assuming that s is a point in the study area, the forecasting result at location s can be expressed as follows (Liu et al., 2021):
$$ {W_s} = \sum\limits_r {{\lambda _r}{f_r} \left( {{t_s}} \right)} , $$ (11) where
${W_s}$ is the forecasting results of surface currents at point s; r represents the representative point number of the area to which point s belongs, taking values 1, 2, 3, 4, and 5, corresponding to P1, P2, P3, P4, and P5 respectively; fr(t) is the model at point Pi;${t_s}$ is the forecasting features at point s;${\lambda _r}$ representing the weights is defined as$$ {\lambda _r} = {{\frac{1}{{{d_r}}}}}\left/{{\sum\limits_r {\frac{1}{{{d_r}}}} }} \right., $$ (12) where dr is the distance from point s to point Pi. Forecasting of all 715 observation points are obtained by accumulating the forecasting results of Mp1–Mp5 after assigning weights.
By combining the inverse distance weighting method with the forecasting results of application model at representative points (Fig. 6), the forecasting and HFR observations are shown in Fig. 7. Through weight calculation, the forecasting of surface currents in the eight sub-areas Z1–Z8 has good agreement with observed data. It can be seen that the high-precision surface current field replicates the overall eastward flow trend and the inshore tidal currents in the nearshore area.
3.2 Forecasting of surface current velocities at multi time-steps
3.2.1 Forecasting of surface current velocities at multi time-steps at representative points
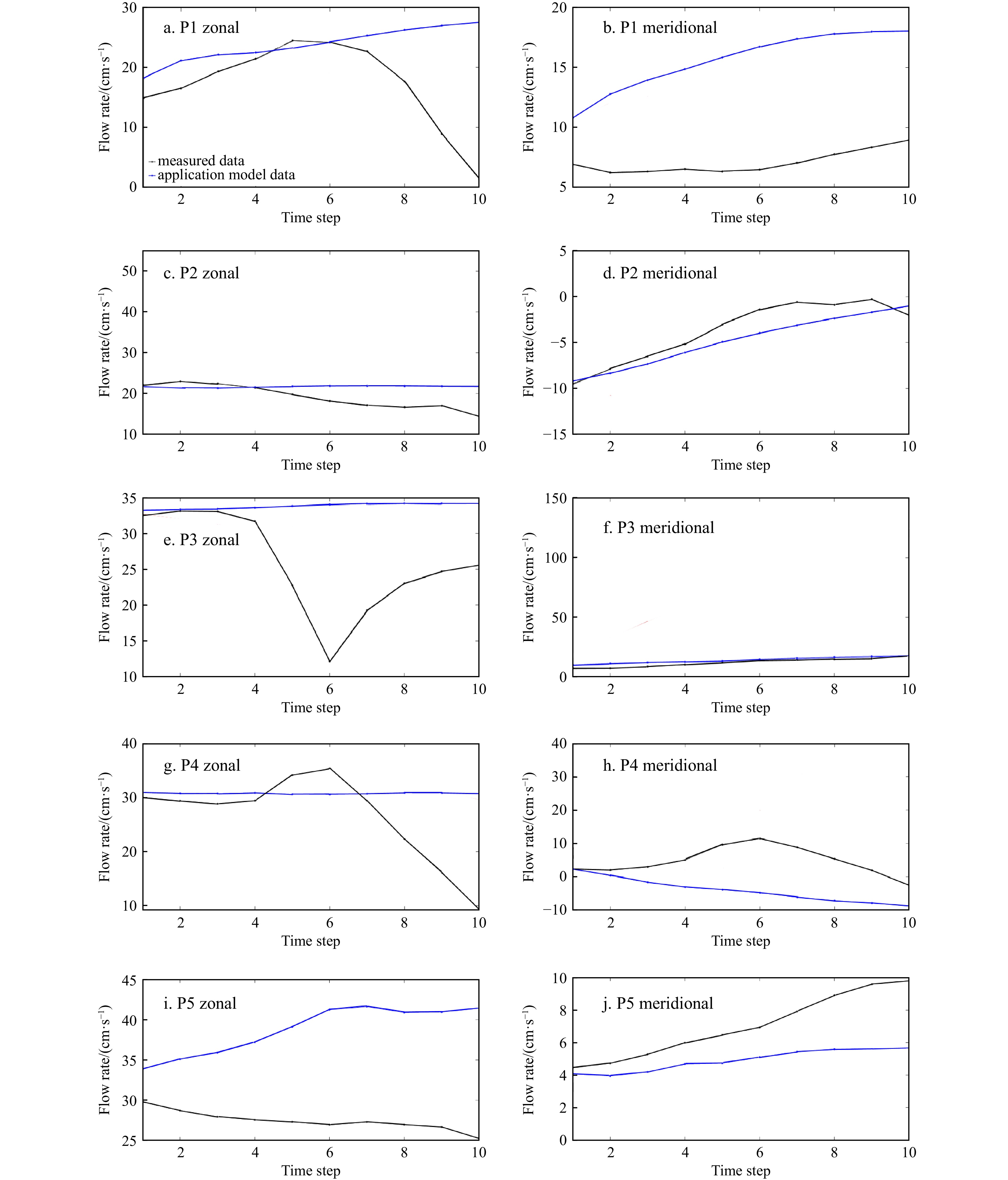
The application model based on the ensemble algorithm generate satisfactory surface current forecasting at single time-step, but multi time-steps forecasting information of surface currents are more useful and are needed in practical engineering applications. Thus, the forecasting and analysis of the sea surface current velocities for subsequent steps were performed in rolling forecasting models. Figure 8 shows the rolling forecasting results of sea surface current zonal and meridional components at P1–P5. It is difficult to portray the trend of surface current velocity changes in forecasting surface currents in the application model, and it only continues the trend of surface current velocity at the input end, which leads to a significant decrease in the accuracy of the application model when the surface currents are more variable. The application model performs similarly in all the forecasting at the representative points, with a monotonic trend in the forecasting surface current velocities. In Figs 8d and f, the measured surface currents vary smoothly with a certain trend, forecasting results of the application model is high. But in Fig. 8e, the trend of the measured surface currents decreases and then increases, and the trend of the forecasting surface currents of the application model increases slowly, and the application model cannot reflect the variation of the surface currents, and the MAE is relatively large. The application model has large variability. Therefore, in order to improve the forecasting ability of the model, the following study focuses on improving the model structure and input variable selection by combining the characteristics of surface currents, reconstructing models for different forecasting time-steps and optimizing the forecasting results.
Different historical surface currents and wind speed data are available at different time steps. If the forecasting features do not vary with the increase of forecast steps, the forecast errors increase. Therefore, the forecasting model was reconstructed according to the characteristics of surface currents in combination with the ensemble algorithm. RF was used for each time-step to evaluate the importance of the features and select the features dynamically. The forecasting results are presented in Table 6 and Table 7. Forecasting accuracy decreases gradually with the increase of forecasting time-steps. When the forecasting are 10 time-steps, the optimal model is the reconstruction model of the meridional component at P1 with RMSE by 2.84 cm/s, correlation coefficient by 0.96 and MAE by 2.02 cm/s. Increasement in the number of forecasting steps leads to a gradual increase in the number of feature inputs to maintain the high forecasting accuracy. This dynamic forecasting factor selection method makes the forecasting ability of the reconstruction forecasting model maintain at a high and stable level.
Table 6. Evaluation of multi time-step forecasting (zonal component of surface velocity)Point Forecasting
stepFeature
numberRMSE/
(cm·s–1)r MAE/
(cm·s–1)P1 2 8 1.82 1.00 1.09 3 8 2.59 1.00 1.61 4 9 3.33 0.99 2.16 5 10 3.93 0.99 2.60 6 12 4.47 0.99 3.02 7 16 4.56 0.99 3.12 8 23 4.60 0.99 3.13 9 32 4.72 0.99 3.27 10 37 4.97 0.99 3.45 P2 2 8 2.51 1.00 1.49 3 9 3.57 0.99 2.16 4 10 4.19 0.99 2.62 5 11 4.69 0.98 3.02 6 16 4.91 0.98 3.17 7 25 4.92 0.98 3.26 8 33 4.81 0.98 3.27 9 39 4.97 0.98 3.40 10 43 5.01 0.98 3.5 P3 2 8 1.70 1.00 0.99 3 8 2.27 1.00 1.40 4 9 2.83 0.99 1.80 5 10 3.29 0.99 2.19 6 13 3.61 0.99 2.45 7 18 3.52 0.99 2.39 8 26 3.67 0.99 2.50 9 34 3.74 0.99 2.62 10 43 3.93 0.99 2.81 P4 2 12 3.84 0.99 2.18 3 22 4.74 0.98 2.78 4 35 5.30 0.97 3.21 5 48 5.60 0.97 3.48 6 58 5.71 0.97 3.65 7 66 5.41 0.97 3.54 8 74 5.58 0.97 3.68 9 80 5.67 0.97 3.79 10 85 5.84 0.97 3.92 P5 2 58 4.48 0.97 2.72 3 85 5.51 0.95 3.46 4 100 5.80 0.95 3.75 5 108 6.08 0.94 4.02 6 114 6.00 0.94 4.04 7 118 6.29 0.94 4.24 8 120 6.39 0.94 4.36 9 122 6.43 0.94 4.40 10 123 6.68 0.93 4.61 Table 7. Evaluation of multi time-step forecasting (meridional component of surface velocity)Point Forecasting
stepFeature
numberRMSE/
(cm·s–1)r MAE/
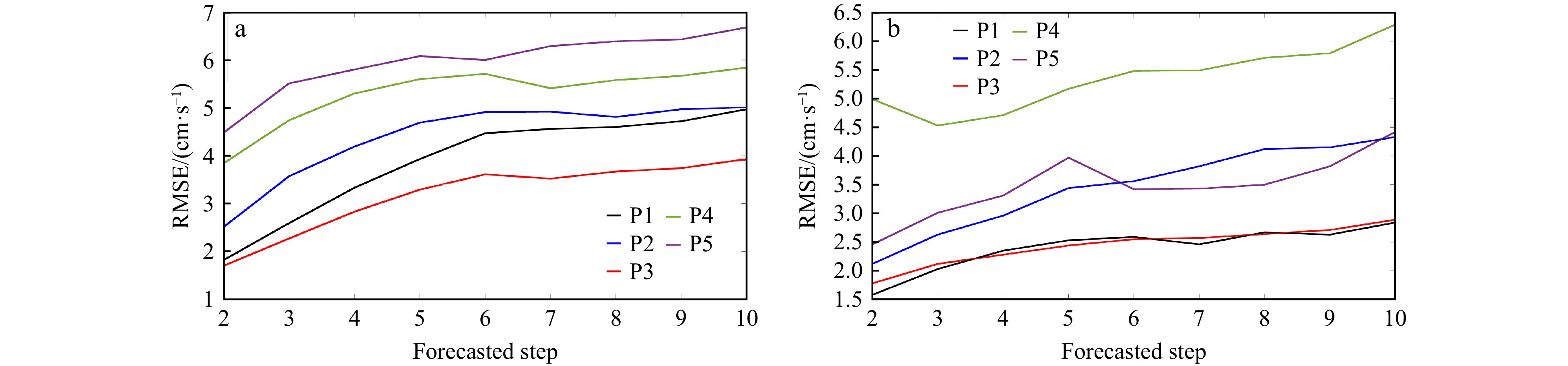
(cm·s–1)P1 2 9 1.58 0.99 0.78 3 25 2.03 0.98 1.08 4 40 2.35 0.97 1.35 5 56 2.53 0.97 1.54 6 74 2.59 0.97 1.67 7 89 2.46 0.97 1.68 8 102 2.67 0.97 1.85 9 111 2.63 0.97 1.87 10 117 2.84 0.96 2.02 P2 2 18 2.12 0.98 1.24 3 46 2.63 0.97 1.66 4 72 2.96 0.96 1.99 5 90 3.44 0.95 2.30 6 102 3.56 0.95 2.54 7 112 3.82 0.94 2.63 8 176 4.12 0.93 2.88 9 126 4.15 0.93 2.90 10 131 4.33 0.92 3.02 P3 2 10 1.78 0.99 0.82 3 19 2.12 0.98 1.08 4 36 2.28 0.98 1.24 5 53 2.44 0.97 1.40 6 65 2.55 0.97 1.54 7 76 2.57 0.97 1.62 8 86 2.64 0.97 1.72 9 93 2.71 0.97 1.79 10 100 2.89 0.96 1.95 P4 2 84 4.99 0.92 3.08 3 109 4.53 0.93 2.82 4 121 4.71 0.93 2.96 5 129 5.17 0.91 3.27 6 134 5.48 0.90 3.55 7 137 5.49 0.90 3.62 8 141 5.71 0.89 3.75 9 143 5.79 0.89 3.85 10 145 6.29 0.87 4.15 P5 2 40 2.46 0.97 1.29 3 67 3.01 0.96 1.67 4 83 3.31 0.95 1.94 5 95 3.97 0.93 2.36 6 104 3.42 0.95 2.18 7 111 3.43 0.95 2.28 8 116 3.50 0.95 2.34 9 121 3.82 0.94 2.60 10 125 4.42 0.91 3.01 The RMSE of the multi time-step forecasting results of the zonal and meridional components are shown in Fig. 9. Results indicate that the forecasting ability of the reconstruction model decreases with the extension of the forecasting window period. However, when the forecasting time is 10 time-steps, the RMSE is still less than 7.00 cm/s, lower than the 16 cm/s predicted by Aydoğan et al. (2010) using FFBP-ANN model. It can be seen from Fig. 9a that the RMSE value increases gradually with the increase of the number of forecasting steps, and the increase is greater when there are few forecasting steps. After the forecasting length was extended to 6 time-steps, variation of RMSE becomes flat and even decreases at some representative points. Since HFR observations have high accuracy and strong continuity, when the number of forecasting length is short, variation trend of surface currents can be well captured by the models. Increasement of forecasting steps has little effects on the data continuity of the forecasting. Gradual stabilization of subsequent errors better reflect the stability of the reconstruction application model based on ensemble learning after the forecasting windows were extended.
It can be seen that P3 has the strongest predictability, followed by P1 and P2, and then points P4 and P5. Combined with the spatial position of the five representative points, P1 and P2 are close to the land. Water depth is shallow and there are some surrounding islands. Marine hydrodynamic processes are more complex in this area, which makes it more difficult to forecast. P3 is located in the core area of radar observation, the input data are of high quality and it is distant from the coast. Surface currents are affected by the features to a less extent than others, so the forecasting accuracy is higher than others. P4 and P5 are far away from the shore. Surface seawater is less affected by the shore boundaries and the bottom boundaries than P1 and P2. However, because P4 and P5 are far from the two observation radar stations, the data are not as good as P1 and P2 in quality and completeness. According to the characteristics of HFR surface currents, the accuracy of the sea current velocity extracted from the radar echo signal decreases with increasing distance, and the range of the missing data is also increasing (Li et al., 2017). In the subsequent process of filling the data through various methods, it inevitably brings errors, which directly have influence on the forecasting results, and even bring greater forecasting errors. Figure 9b shows that except point P4, the multi time-step forecasting of the representative points is better in meridional component than that of zonal component. Forecasting accuracy of meridional component at P5 is significantly higher than that of zonal component. Its accuracy is close to that of meridional component at point P2. With the increase of forecasting steps, the curve of P5 intersects P2 and even lower than P2.
3.2.2 Forecasting of surface current fields in multi time-steps
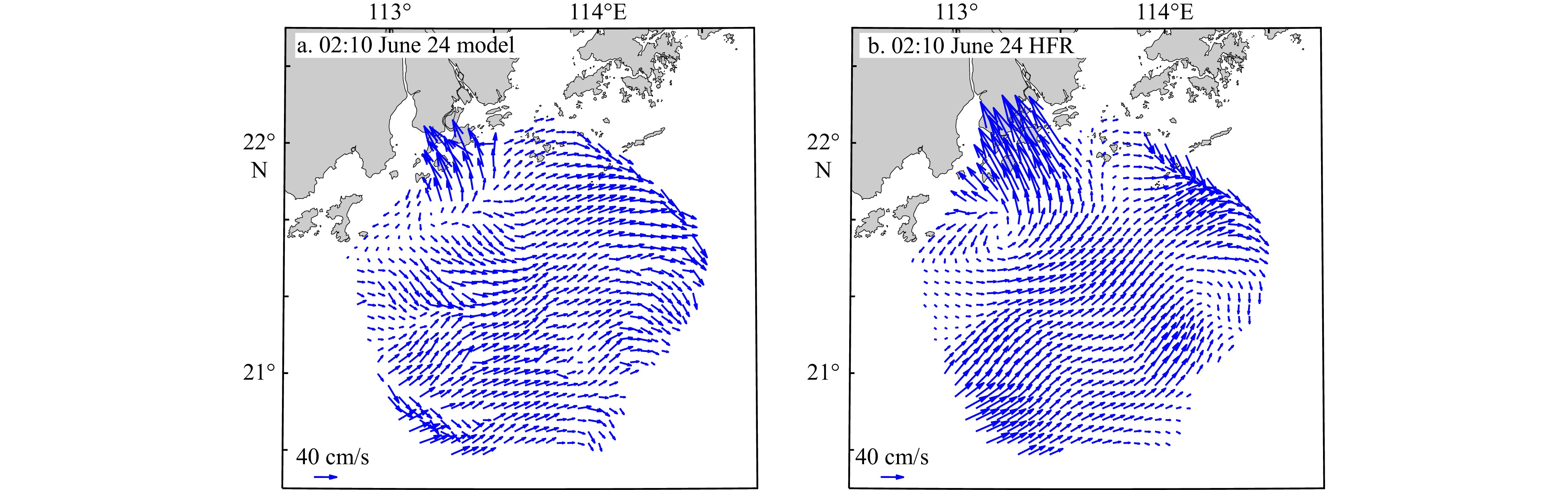
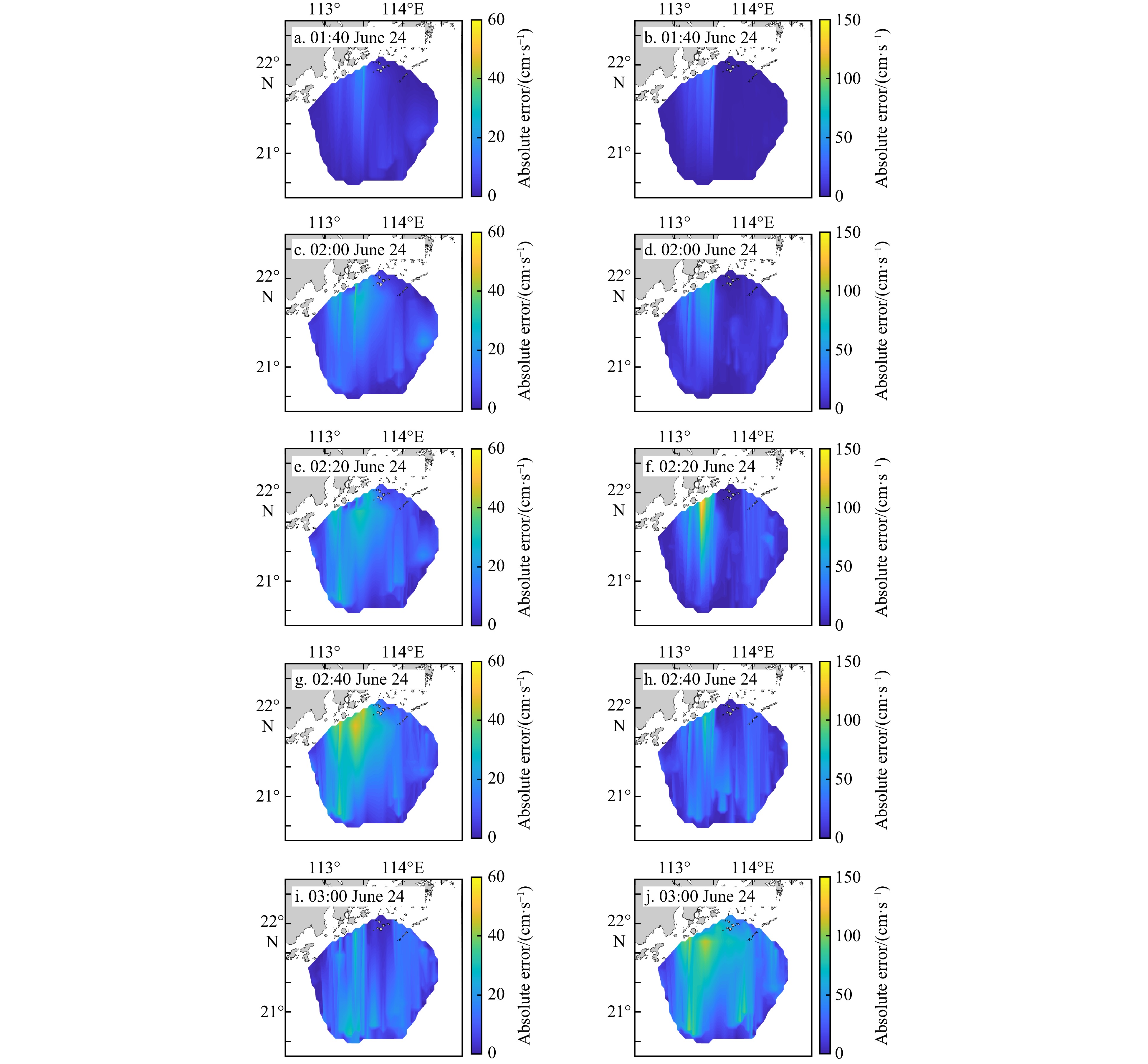
After obtaining the reconstruction model for each forecasting time-step, the current field forecasting over a long window period can be obtained by applying the point-to-surface expansion method. If the present time is 01:30 (UTC+8) on June 24, 2021, based on the HFR observations at and before this time, the wind speeds from the ECMWF, surface current fields at ten time-steps ahead were obtained, as shown in Fig. 10. It can be found that the surface current fields from 01:40 (UTC+8) to 03:10 (UTC+8) generally have a northeastern flow trend. This forecasting period is located in the flood tide stage. Flow direction of the surface currents in the northwest coastal areas is toward the shore, and flow direction in the northeast areas along the island chain areas is generally southeastward. Eddies in the western areas existed and the vortex center tended to move eastward. A new eddy gradually formed in the southeastern areas at nearly 03:00 (UTC+8). Additionally, the model can generate northeastward flows during the period. Forecasted surface currents in the northwest nearshore areas always flow in the inshore direction. The southeastward surface currents in the northeast island chain areas also have a good agreement with HFR observations. Eddies in the northwest disappear at the fourth forecasting time-step. With the increasement of forecasting time-steps, there is a chaotic streamline at the edge of the surface current fields, especially in the southern areas. Focusing on the overall surface current fields, the boundaries between the eastern and western areas due to zoning is gradually significant. Although the forecasting window is 10 time-steps, the application model still well captures the overall surface flow trend. In the case when the forecasting window is 3 time-steps, the forecasting has the highest accuracy. For 4 to 10 forecasting time-steps, the model generates surface currents with a good agreement with observations in flow trend.
4. Discussion
In this study, forecasting of surface current velocities based on an ensemble learning algorithm in combination AdaBoost with RF. Input variables are the historical current data observed by HFR and 10 m wind speed data provided by ECMWF. For the zonal component, the point P1 has the optimal effect of forecasting, RMSE by 0.95 cm/s, correlation coefficient close to 1, and MAE by 0.62 cm/s; for the meridional component, similarly, the point P1 has the optimal effect of forecasting, with RMSE by 0.87 cm/s, correlation coefficient close to 1, and MAE by 0.40 cm/s. Ren et al. (2018) used historical radar data, wind data and tidal data to build a model with the error backward transfer artificial neural network algorithm, which produced accurate outputs within a short-term forecasting window. In this study, the higher forecast accuracy was achieved with less input data, which highlights the advantages of the ensemble algorithm for surface current forecasting.
Aydoğan et al. (2010) developed the FFBP-ANN models for forecasting and the RMSE between forecasting results and observations is 16 cm/s. Bradbury and Conley (2021) used the HFR observations as input to forecast the subsurface currents and the MAE is 5 cm/s. Forecasting accuracy in this research has a huge advantage of one to two orders of magnitude compared with them. The basis of machine learning application in physical ocean fields still rely on high quality observation data, reliable numerical model and deep understanding of physical ocean principles. It is necessary to choose the appropriate machine learning method according to different application scenarios combined with physical mechanisms. Besides the advantages of the models and algorithms themselves, the high forecasting accuracy in this study is to some extent due to the selection procedure of input variables. Additionally, in term of RMSE values between forecasting and observations, short-term forecasting using the developed machine learning model in this research outperformed the self-organizing map-based forecast and ROMS model (Vilibić et al., 2016).
In addition to forecast the surface current patterns, trends of surface currents and ocean physical phenomena, so as to provide guidance and basis for route planning and coastal island engineering construction and so on. In order to further analyze the accuracy of multi time-step forecasting of the surface current fields using the reconstruction model, the absolute errors of the zonal and meridional components between forecasting and HFR observations at each observation point of the measured current field are shown in Fig. 11 (interval is two time-steps). Forecasting accuracy in the nearshore areas is low at the 5th forecasting time-steps. Although the surface flow direction and flood tide states can be well predicted, the difference is especially significant in the areas near the Modaomen estuary. The absolute error of the zonal component is greater than 50 cm/s and the absolute error of the meridional component is greater than 100 cm/s. This may be due to following reasons: (1) the northwestern part of the study area is close to the land and coast, with complex topographic conditions and shallow water depth, the movement of surface currents is influenced by the land boundary, bottom boundary and the dynamic processes is more complex; (2) this area is influenced by river runoff from the Modaomen estuary, the surface currents are affected (Xie et al., 2015); (3) the area is located on the line of two radar stations, accuracy of the total surface current vectors synthesized from two radars is low, which may lead to the decrease of the predictability of surface currents (Port et al., 2011).
Except for the northwestern part of the study area where the absolute error is significantly greater than others, the absolute error of the zonal component is still larger than that of meridional component. This may be due to that two radar stations were deployed in the northwestern and northeastern parts of the study area, resulting in the poor inversion of signals. The analysis of regional surface currents in this study is based on the HFR observations, but due to the limitations of the radar data itself, the inversion of echo signals in areas farther away from the stations is poorer than other areas. Additionally, the radar observation principle is based on vector synthesis and decomposition, the current measurement data within the straight line of the two radars will be less accurate (Paduan and Washburn, 2013).
In comparison with previous studies on ocean current forecasting, there are two significant innovations in this research. Firstly, multi strategy feature parameter selection methods had been applied in model construction to avoid errors caused by empirical selection. Secondly, the abundant observation data from HFR system provides feasibility for constructing machine learning ocean surface current forecasting models at multiple representative points, and helps to verify the effectiveness and scalability of the model construction framework. Thus, utilization of machine learning algorithms and HFR observation is a potential and useful means can to generate forecasting information of surface currents in coastal areas. This research is a good test for its applicability and effectiveness. It can be used in other coastal areas and other marine environmental parameters such as wave, tide and wind. It should be noted that although Random Forests can evaluate the importance of features, in practical applications, the feature selection process may involve subjective judgment, such as setting a threshold for feature importance. Moreover, random forests have a certain degree of robustness, in some cases, they may be overly sensitive to noise and outliers in the data, which may affect the forecasting performance.
5. Conclusions
Based on the analysis of the spatial and temporal characteristics of the sea surface currents in the GBA, this study constructed forecasting models of coastal surface currents and extended the model forecasting ability from single point and single time-step to multi time-steps in space. The developed forecasting model has advantages of relatively simple construction process, low computational cost and high short-term forecast accuracy. The main conclusions are as follows:
(1) The semidiurnal and diurnal components of tide currents are the main influencing factors at representative points. Shallow water effect is significant.
(2) The application model based on the ensemble algorithm produced satisfactory sea surface current forecasting at a single time step. However, in the rolling multi time-step forecasting, the application model is not effective in forecasting sea surface currents with large variability. Application models is a efficient way to improve the forecasting ability.
(3) When the forecast window is 10 time-steps, the overall trend of the surface current fields obtained by the ensemble-based algorithm is consistent with the measured current field, but the difference with the measured data is more significant in the northwestern sea area, which may be influenced by the topography of the study area, the boundary and the geometric accuracy of the observation system.
The next step is to consider selecting a larger number of representative points, especially in the nearshore area where the current velocities are influenced by the interaction of multiple features. It is necessary to further optimize forecasting capability of models and improve the reliability of the model for short-term forecasting and current field forecasting. In future research, it needs to consider introducing other current measurement such as ADCP and buoys or combining them with numerical forecasting models, which is important for the subsequent improvement of the forecast accuracy in these areas.
Acknowledgement: We would like to thank ECMWF for providing wind data. -
Table 1. Statistics of tidal ellipticity, tidal type coefficients and shallow water coefficients
Point Tidal ellipticity Tidal type
coefficientShallow water
coefficientO1 K1 M2 S2 P1 –0.4 –0.06 –0.22 0.12 1.51 0.32 P2 –0.10 –0.11 –0.02 0.21 1.11 0.20 P3 –0.07 –0.2 –0.02 0.29 1.09 0.20 P4 0.22 –0.34 –0.05 –0.12 1.27 0.19 P5 –0.37 –0.27 –0.31 0.44 1.68 0.24 Table 2. Statistics of the optimal correlation coefficients of surface current components
Point Correlation coefficient Lag time/h Zonal component Meridional component Zonal component Meridional component P1 0.75 0.31 12 11 P2 0.78 0.31 12 8 P3 0.79 0.22 11 9 P4 0.68 0.24 9 9 P5 0.55 –0.09 11 9 Table 3. Forecasting model set-up
Model Algorithm Feature Feature selection Forecasting model Baseline model \ AdaBoost total observation data Application model random forest AdaBoost observation data whose total variable importance accumulates over 95% Rolling model random forest AdaBoost observation data whose importance accumulates over 95% at the first time-step Reconstruction model random forest AdaBoost observation data whose importance accumulates over 95% at each time-step Note: \ denotes no feature selection. Table 4. Assessment statistics of single time-step forecasting (training dataset)
Point Zonal component of surface velocity assessment statistic Meridional component of surface velocity assessment statistic Feature number RMSE/(cm·s–1) R MAE/(cm·s–1) Feature number RMSE/(cm·s–1) R MAE/(cm·s–1) P1 176 0.96 1.00 0.55 176 0.87 1.00 0.40 8 1.04 1.00 0.58 8 0.94 1.00 0.58 P2 176 1.46 1.00 0.82 176 1.31 0.99 0.73 9 1.56 1.00 0.85 8 1.42 0.99 0.76 P3 176 0.96 1.00 0.52 176 1.06 1.00 0.45 8 1.04 1.00 0.55 8 1.14 0.99 0.46 P4 176 2.41 0.99 1.29 176 2.52 0.98 1.35 9 2.60 0.99 1.36 36 2.68 0.98 1.36 P5 176 3.55 0.98 2.11 176 1.69 0.99 0.81 13 4.06 0.98 2.16 13 1.80 0.99 0.85 Table 5. Assessment statistics of single time-step forecasting (test dataset)
Point Zonal component of surface velocity assessment statistic Meridional component of surface velocity assessment statistic Feature number RMSE/(cm·s–1) R MAE/(cm·s–1) Feature number RMSE/(cm·s–1) R MAE/(cm·s–1) P1 8 0.95 1.00 0.62 8 1.66 0.99 0.67 P2 9 2.41 0.99 1.00 8 2.05 0.98 0.85 P3 8 1.55 1.00 0.71 8 3.68 0.97 1.04 P4 9 5.02 0.98 1.62 36 9.36 0.94 3.29 P5 13 2.97 0.98 1.75 10 1.90 0.99 0.84 Table 6. Evaluation of multi time-step forecasting (zonal component of surface velocity)
Point Forecasting
stepFeature
numberRMSE/
(cm·s–1)r MAE/
(cm·s–1)P1 2 8 1.82 1.00 1.09 3 8 2.59 1.00 1.61 4 9 3.33 0.99 2.16 5 10 3.93 0.99 2.60 6 12 4.47 0.99 3.02 7 16 4.56 0.99 3.12 8 23 4.60 0.99 3.13 9 32 4.72 0.99 3.27 10 37 4.97 0.99 3.45 P2 2 8 2.51 1.00 1.49 3 9 3.57 0.99 2.16 4 10 4.19 0.99 2.62 5 11 4.69 0.98 3.02 6 16 4.91 0.98 3.17 7 25 4.92 0.98 3.26 8 33 4.81 0.98 3.27 9 39 4.97 0.98 3.40 10 43 5.01 0.98 3.5 P3 2 8 1.70 1.00 0.99 3 8 2.27 1.00 1.40 4 9 2.83 0.99 1.80 5 10 3.29 0.99 2.19 6 13 3.61 0.99 2.45 7 18 3.52 0.99 2.39 8 26 3.67 0.99 2.50 9 34 3.74 0.99 2.62 10 43 3.93 0.99 2.81 P4 2 12 3.84 0.99 2.18 3 22 4.74 0.98 2.78 4 35 5.30 0.97 3.21 5 48 5.60 0.97 3.48 6 58 5.71 0.97 3.65 7 66 5.41 0.97 3.54 8 74 5.58 0.97 3.68 9 80 5.67 0.97 3.79 10 85 5.84 0.97 3.92 P5 2 58 4.48 0.97 2.72 3 85 5.51 0.95 3.46 4 100 5.80 0.95 3.75 5 108 6.08 0.94 4.02 6 114 6.00 0.94 4.04 7 118 6.29 0.94 4.24 8 120 6.39 0.94 4.36 9 122 6.43 0.94 4.40 10 123 6.68 0.93 4.61 Table 7. Evaluation of multi time-step forecasting (meridional component of surface velocity)
Point Forecasting
stepFeature
numberRMSE/
(cm·s–1)r MAE/
(cm·s–1)P1 2 9 1.58 0.99 0.78 3 25 2.03 0.98 1.08 4 40 2.35 0.97 1.35 5 56 2.53 0.97 1.54 6 74 2.59 0.97 1.67 7 89 2.46 0.97 1.68 8 102 2.67 0.97 1.85 9 111 2.63 0.97 1.87 10 117 2.84 0.96 2.02 P2 2 18 2.12 0.98 1.24 3 46 2.63 0.97 1.66 4 72 2.96 0.96 1.99 5 90 3.44 0.95 2.30 6 102 3.56 0.95 2.54 7 112 3.82 0.94 2.63 8 176 4.12 0.93 2.88 9 126 4.15 0.93 2.90 10 131 4.33 0.92 3.02 P3 2 10 1.78 0.99 0.82 3 19 2.12 0.98 1.08 4 36 2.28 0.98 1.24 5 53 2.44 0.97 1.40 6 65 2.55 0.97 1.54 7 76 2.57 0.97 1.62 8 86 2.64 0.97 1.72 9 93 2.71 0.97 1.79 10 100 2.89 0.96 1.95 P4 2 84 4.99 0.92 3.08 3 109 4.53 0.93 2.82 4 121 4.71 0.93 2.96 5 129 5.17 0.91 3.27 6 134 5.48 0.90 3.55 7 137 5.49 0.90 3.62 8 141 5.71 0.89 3.75 9 143 5.79 0.89 3.85 10 145 6.29 0.87 4.15 P5 2 40 2.46 0.97 1.29 3 67 3.01 0.96 1.67 4 83 3.31 0.95 1.94 5 95 3.97 0.93 2.36 6 104 3.42 0.95 2.18 7 111 3.43 0.95 2.28 8 116 3.50 0.95 2.34 9 121 3.82 0.94 2.60 10 125 4.42 0.91 3.01 -
Ali J, Khan R, Ahmad N, et al. 2012. Random forests and decision trees. International Journal of Computer Science Issues, 9(5): 272–278 Aydoğan B, Ayat B, Öztürk M N, et al. 2010. Current velocity forecasting in straits with artificial neural networks, a case study: Strait of Istanbul. Ocean Engineering, 37(5/6): 443–453, doi: 10.1016/j.oceaneng.2010.01.016 Barrick D E, Headrick J M, Bogle R W, et al. 1974. Sea backscatter at HF: Interpretation and utilization of the echo. Proceedings of the IEEE, 62(6): 673–680, doi: 10.1109/PROC.1974.9507 Basañez A, Pérez-Muñuzuri V. 2021. HF radars for wave energy resource assessment offshore NW Spain. Remote Sensing, 13(11): 2070, doi: 10.3390/rs13112070 Bradbury M C, Conley D C. 2021. Using artificial neural networks for the estimation of subsurface tidal currents from high-frequency radar surface current measurements. Remote Sensing, 13(19): 3896, doi: 10.3390/rs13193896 Breiman L. 2001. Random forests. Machine Learning, 45(1): 5–32, doi: 10.1023/A:1010933404324 Chen Yuru, Paduan J D, Cook M S, et al. 2021. Observations of surface currents and tidal variability off of northeastern taiwan from shore-based high frequency radar. Remote Sensing, 13(17): 3438, doi: 10.3390/rs13173438 Cheng Peng, Valle-Levinson A. 2009. Influence of lateral advection on residual currents in microtidal estuaries. Journal of Physical Oceanography, 39(12): 3177–3190, doi: 10.1175/2009JPO4252.1 Cosoli S, Pattiaratchi C, Hetzel Y. 2020. High-frequency radar observations of surface circulation features along the south-western Australian coast. Journal of Marine Science and Engineering, 8(2): 97, doi: 10.3390/jmse8020097 Dinh V N, McKeogh E. 2019. Offshore wind energy: technology opportunities and challenges. In: Proceedings of the 1st Vietnam Symposium on Advances in Offshore Engineering. Singapore: Springer Fang Shenguang, Xie Yufeng, Cui Liqin. 2015. Analysis of tidal prism evolution and characteristics of the Lingdingyang Bay at Pearl River estuary. MATEC Web of Conferences, 25: 01006, doi: 10.1051/matecconf/20152501006 Han Qinghua, Gui Changqing, Xu Jie, et al. 2019. A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Construction and Building Materials, 226: 734–742, doi: 10.1016/j.conbuildmat.2019.07.315 Hastie T, Tibshirani R, Friedman J. 2009. Random forests. In: Hastie T, Tibshirani R, Friedman J, eds. The Elements of Statistical Learning. New York: Springer, 587–604 Immas A, Do N, Alam M R. 2021. Real-time in situ prediction of ocean currents. Ocean Engineering, 228: 108922, doi: 10.1016/j.oceaneng.2021.108922 Jishun R. 1991. On the geotectonics of southern China. Acta Geologica Sinica-English Edition, 4(2): 111–130, doi: 10.1111/j.1755-6724.1991.mp4002001.x Johnston K, Ver Hoef J M, Krivoruchko K, et al. 2001. Using ArcGIS Geostatistical Analyst. Redlands: Esri Redlands Kim S J, Kõrgersaar M, Ahmadi N, et al. 2021. The influence of fluid structure interaction modelling on the dynamic response of ships subject to collision and grounding. Marine Structures, 75: 102875, doi: 10.1016/j.marstruc.2020.102875 Klemas V. 2011. Remote sensing techniques for studying coastal ecosystems: an overview. Journal of Coastal Research, 27(1): 2–17 Li Ruixiang, Chen Changsheng, Xia Huayong, et al. 2014. Observed wintertime tidal and subtidal currents over the continental shelf in the northern South China Sea. Journal of Geophysical Research: Oceans, 119(8): 5289–5310, doi: 10.1002/2014JC009931 Li Chuan, Wu Xiongbin, Yue Xianchang, et al. 2017. Extraction of wind direction spreading factor from broad-beam high-frequency surface wave radar data. IEEE Transactions on Geoscience and Remote Sensing, 55(9): 5123–5133, doi: 10.1109/TGRS.2017.2702394 Lin Mingsen, Xu Dewei, Li Xiaosun. 2003. Application of satellite data in monsoon and circulation of south China sea. In: Proceedings of SPIE 4892, Ocean Remote Sensing and Applications. Hangzhou: SPIE Liu Qinyu, Kaneko A, Jilan S. 2008. Recent progress in studies of the South China Sea circulation. Journal of Oceanography, 64(5): 753–762, doi: 10.1007/s10872-008-0063-8 Liu Zhen, Zhang Zhilong, Zhou Cuiying, et al. 2021. An adaptive inverse-distance weighting interpolation method considering spatial differentiation in 3D geological modeling. Geosciences, 11(2): 51, doi: 10.3390/geosciences11020051 Ma Lei, Fu Tengyu, Blaschke T, et al. 2017. Evaluation of feature selection methods for object-based land cover mapping of unmanned aerial vehicle imagery using random forest and support vector machine classifiers. ISPRS International Journal of Geo-Information, 6(2): 51, doi: 10.3390/ijgi6020051 Mantovani C, Corgnati L, Horstmann J, et al. 2020. Best practices on high frequency radar deployment and operation for ocean current measurement. Frontiers in Marine Science, 7: 210, doi: 10.3389/fmars.2020.00210 Mao Xiaojun, Peng Liuhua, Wang Zhonglei. 2022. Nonparametric feature selection by random forests and deep neural networks. Computational Statistics & Data Analysis, 170: 107436 Mitchell T M. 1999. Machine learning and data mining. Communications of the ACM, 42(11): 30–36, doi: 10.1145/319382.319388 Paduan J D, Washburn L. 2013. High-frequency radar observations of ocean surface currents. Annual Review of Marine Science, 5: 115–136, doi: 10.1146/annurev-marine-121211-172315 Port A, Gurgel K W, Staneva J, et al. 2011. Tidal and wind-driven surface currents in the German Bight: HFR observations versus model simulations. Ocean Dynamics, 61(10): 1567–1585, doi: 10.1007/s10236-011-0412-9 Ren Lei, Hartnett M. 2017a. Sensitivity analysis of a data assimilation technique for hindcasting and forecasting hydrodynamics of a complex coastal water body. Computers & GeoSciences, 99: 81–90 Ren Lei, Hartnett M. 2017b. Prediction of surface currents using high frequency CODAR data and decision tree at a marine renewable energy test site. Energy Procedia, 107: 345–350, doi: 10.1016/j.egypro.2016.12.171 Ren Lei, Hu Zhan, Hartnett M. 2018. Short-term forecasting of coastal surface currents using high frequency radar data and artificial neural networks. Remote Sensing, 10(6): 850, doi: 10.3390/rs10060850 Sagi O, Rokach L. 2018. Ensemble learning: A survey. WIREs: Data Mining and Knowledge Discovery, 8(4): e1249, doi: https://doi.org/10.1002/widm.1249 Sun Shuo, Zhang Qianli, Sun Junzhong, et al. 2022. Lead–acid battery SOC Prediction using improved adaBoost algorithm. Energies, 15(16): 5842, doi: 10.3390/en15165842 Vavatsikos A P, Sotiropoulou K F, Tzingizis V. 2022. GIS-assisted suitability analysis combining PROMETHEE II, analytic hierarchy process and inverse distance weighting. Operational Research, 22(5): 5983–6006, doi: 10.1007/s12351-022-00706-0 Vilibić I, Šepić J, Mihanović H, et al. 2016. Self-organizing maps-based ocean currents forecasting system. Scientific Reports, 6: 22924, doi: 10.1038/srep22924 Wang Lina, Cao Yu, Deng Xilin, et al. 2023a. Significant wave height forecasts integrating ensemble empirical mode decomposition with sequence-to-sequence model. Acta Oceanologica Sinica, 42(10): 54–66, doi: 10.1007/s13131-023-2246-y Wang Yuchen, Imai K, Mulia I E, et al. 2023b. Data Assimilation using high-frequency radar for tsunami early warning: a case study of the 2022 Tonga Volcanic Tsunami. Journal of Geophysical Research: Solid Earth, 128(2): e2022JB025153, doi: 10.1029/2022JB025153 Wang Wenxiong, Rainbow P S. 2020. Environmental Pollution of the Pearl River Estuary, China. Berlin: Springer Wang Shuangling, Zhou Fengxia, Chen Fajin, et al. 2021. Spatiotemporal distribution characteristics of nutrients in the drowned tidal inlet under the influence of tides: a case study of Zhanjiang Bay, China. International Journal of Environmental Research and Public Health, 18(4): 2089, doi: 10.3390/ijerph18042089 Wei Xing, Cai Shuqun, Zhan Weikang. 2021. Impact of anthropogenic activities on morphological and deposition flux changes in the Pearl River Estuary, China. Scientific Reports, 11(1): 16643, doi: 10.1038/s41598-021-96183-0 Wen Xuezhi, Shao Ling, Xue Yu, et al. 2015. A rapid learning algorithm for vehicle classification. Information Sciences, 295: 295–406, doi: 10.1016/j.ins.2014.10.040 Xie Lili, Liu Xia, Yang Qingshu, et al. 2015. Variations of current and sediment transport in Lingding Bay during spring tide in flood season driven by human activities. Journal of Sediment Research (in Chinese), (3): 56–62 Yang Yun. 2017. Temporal Data Mining via Unsupervised Ensemble Learning. Amsterdam: Elsevier Yang Liling, Yang Fang, Yu Shunchao, et al. 2021. The hydrodynamic division of lingdingyang estuary and its application in the impact analysis of large water-related projects. IOP Conference Series: Earth and Environmental Science, 643(1): 012135., doi: 10.1088/1755-1315/643/1/012135 Ye A L, Robinson I S. 1983. Tidal dynamics in the South China Sea. Geophysical Journal International, 72(3): 691–707, doi: 10.1111/j.1365-246X.1983.tb02827.x Yin Xunqiang, Shi Junqiang, Qiao Fangli. 2018. Evaluation on surface current observing network of high frequency ground wave radars in the Gulf of Thailand. Ocean Dynamics, 68(4): 575–587 -





 DownLoad:
DownLoad:

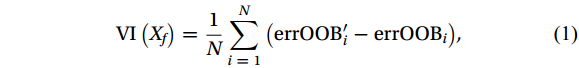
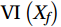
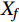
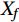


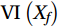
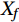
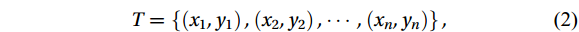
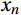

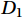

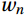
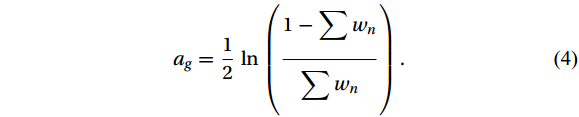
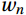
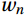
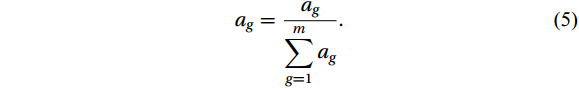
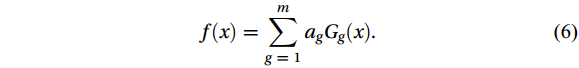
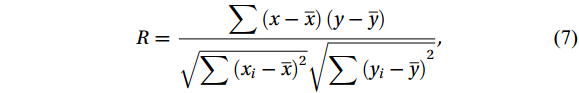
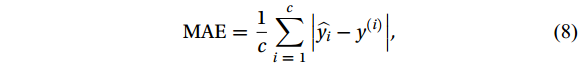
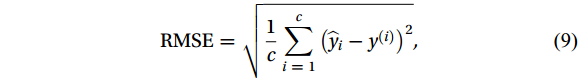
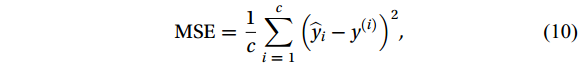

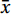
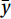

 DownLoad:
DownLoad:

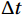




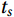

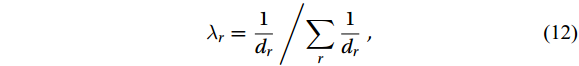







 下载:
下载: