-
Abstract: Coastal wetlands such as salt marshes and mangroves provide important protection against stormy waves. Accurate assessments of wetlands’ capacity in wave attenuation are required to safely utilize their protection services. Recent studies have shown that tidal currents have a significant impact on wetlands’ wave attenuation capacity, but such impact has been rarely considered in numerical models, which may lead to overestimation of wave attenuation in wetlands. This study modified the SWAN (Simulating Waves Nearshore) model to account for the effect of accompanying currents on vegetation-induced wave dissipation. Furthermore, this model was extended to include automatically derived vegetation drag coefficients, spatially varying vegetation height, and Doppler Effect in combined current-wave flows. Model evaluation against an analytical model and flume data shows that the modified model can accurately simulate wave height change in combined current-wave flows. Subsequently, we applied the new model to a mangrove wetland on Hailing Island in China with a special focus on the effect of currents on wave dissipation. It is found that the currents can either increase or decrease wave attenuation depending on the ratio of current velocity to the amplitude of the horizontal wave orbital velocity, which is in good agreement with field observations. Lastly, we used Hailing Island site as an example to simulate wave attenuation by vegetation under hypothetical storm surge conditions. Model results indicate that when currents are 0.08–0.15 m/s and the incident wave height is 0.75–0.90 m, wetlands’ wave attenuation capacity can be reduced by nearly 10% compared with pure wave conditions, which provides implications for critical design conditions for coastal safety. The obtained results and the developed model are valuable for the design and implementation of wetland-based coastal defense. The code of the developed model has been made open source, in the hope to assist further research and coastal management.
-
Key words:
- wave attenuation by vegetation /
- wave-current interaction /
- SWAN model /
- storm waves /
- drag coefficient
-
Figure 1. Wetland ecosystem in combined current-wave flows (a) and wave flume set up (Hu et al., 2014) (b). ADP, RBR, WG, EMF, FT represent Acoustic Doppler Profiler, pressure sensors (RBR solo3), Wave Gauge, electromagnetic flow meter, and force transducer for measuring parameters of currents and waves.
Figure 2. Comparisons of
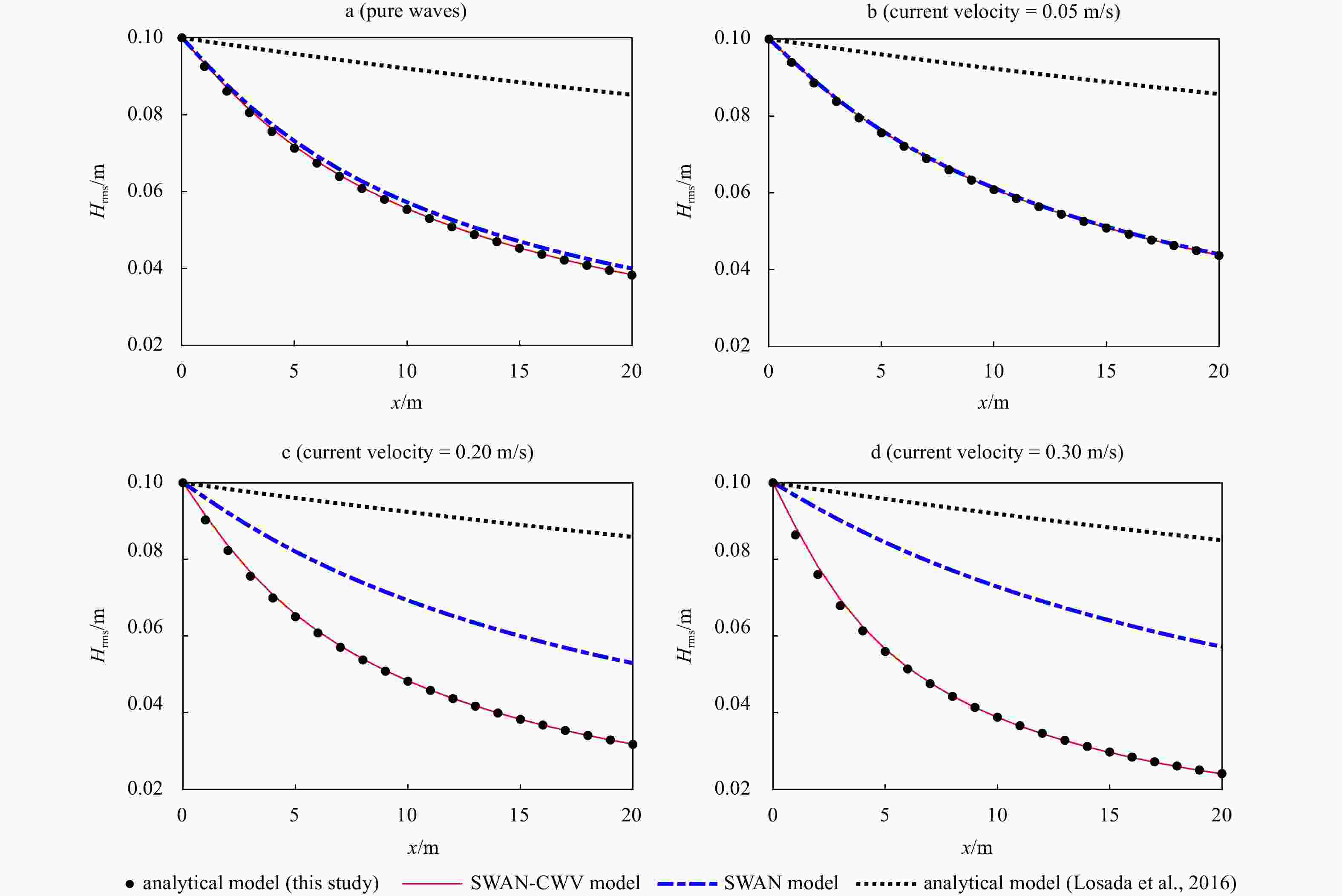
$ {H}_{\mathrm{r}\mathrm{m}\mathrm{s}} $ evolution for SWAN-CWV model with the SWAN model, the analytical model proposed in this study on Eqs (26) and (27), and the analytical model from Losada et al. (2016) with different current velocities. a. Pure waves, b. current velocity = 0.05 m/s, c. current velocity = 0.20 m/s; and d. current velocity = 0.30 m/s. All the tested incident wave height$ {H}_{\mathrm{r}\mathrm{m}\mathrm{s}} $ is 0.1 m and the wave period Tp is 1.5 s. The drag coefficients were all calculated according to the empirical Re-$ {C}_{\mathrm{D}} $ relation on Eq. (16) to exclude the influence of$ {C}_{\mathrm{D}} $ to wave attenuation.Figure 3. Comparisons of the wave height along mimic canopies (green patch) in the current-wave flows (
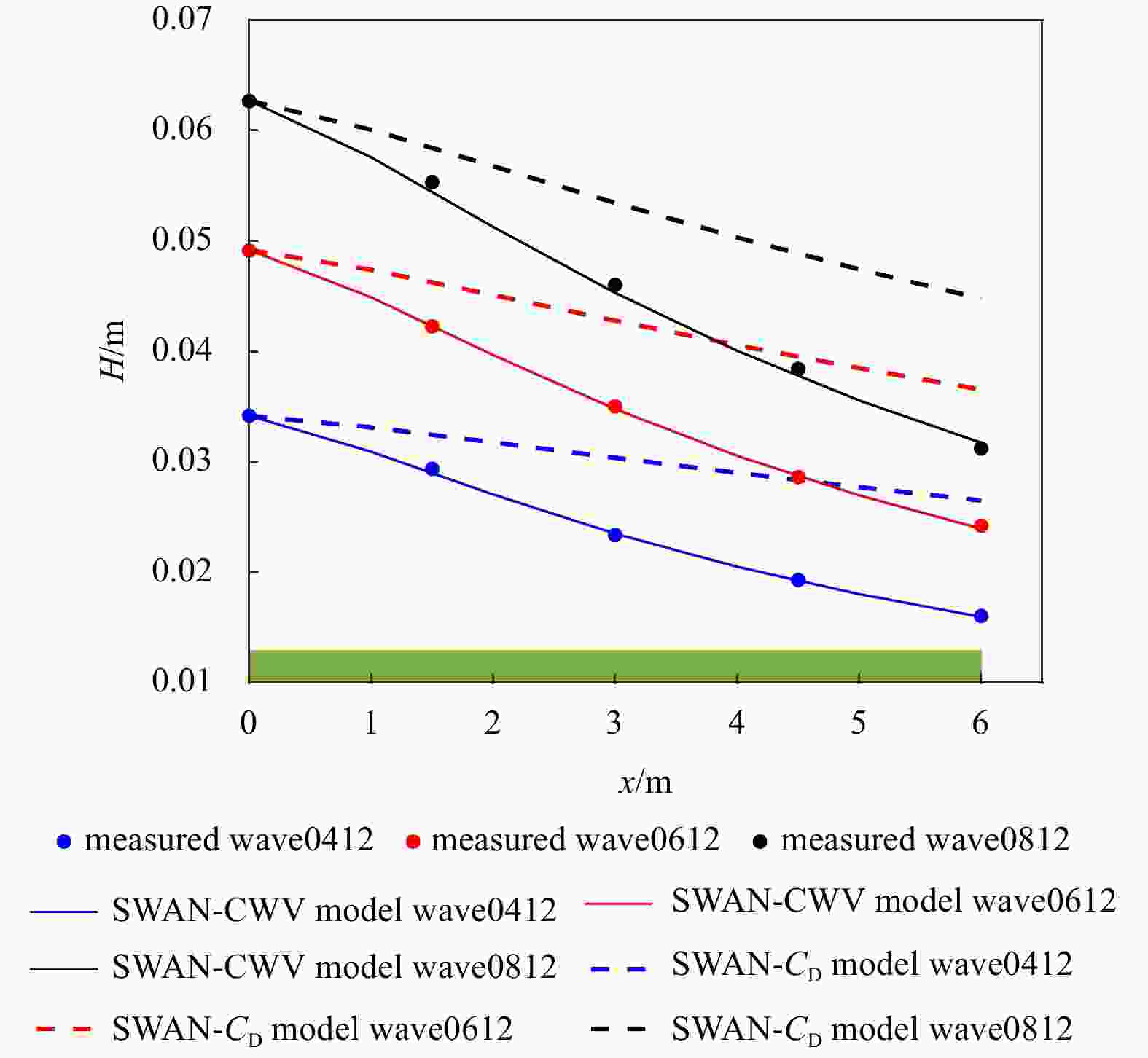
$ {U}_{\mathrm{c}} $ = 0.20 m/s): SWAN-CWV, SWAN-$ {C}_{\mathrm{D}} $ and the measured data (Hu et al., 2014). All cases are in non-submerged canopies with medium mimic stem densities (139 stems/m2). The case name stands for the combination of incident wave height 0.04 m and wave period 1.2 s, namely wave0412.Figure 4. Comparisons of wave height attenuation induced by a unit length of canopies (
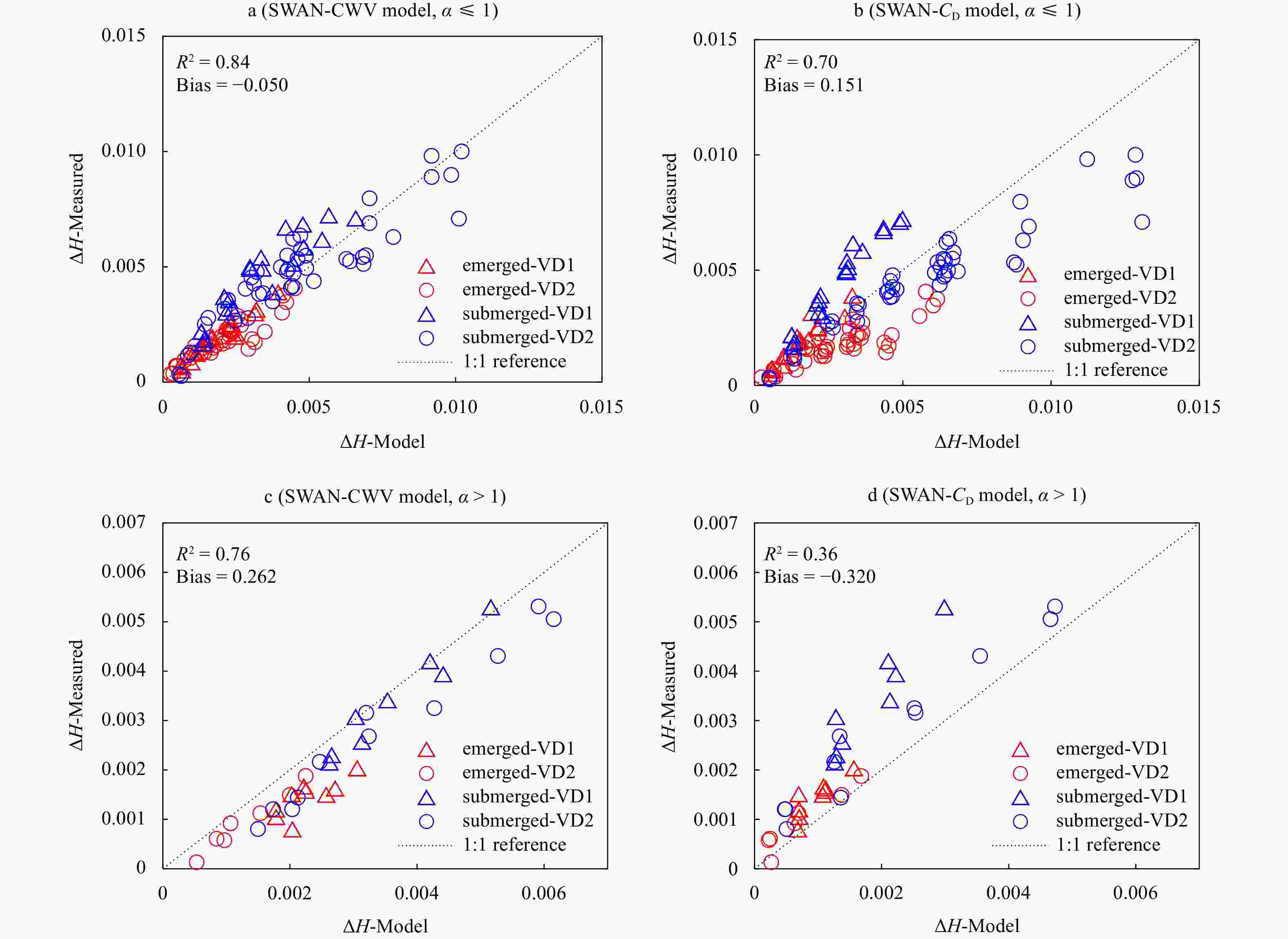
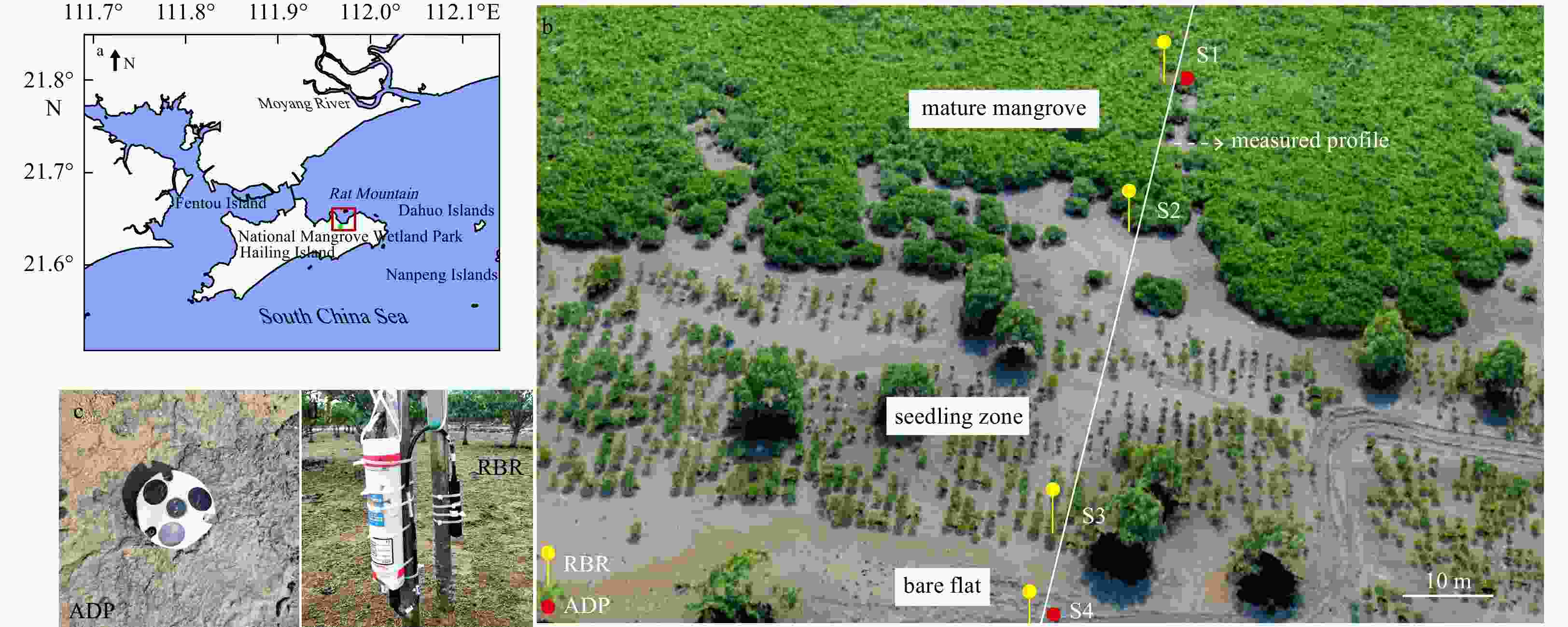
$ \Delta H $ in Eq. (28)) between numerical models (SWAN-CWV and SWAN-$ {C}_{\mathrm{D}} $ ) and experiment data (Hu et al., 2014).Figure 5. The study area (enclosed by the red rectangle) on Hailing Island, South of China (a), top view of the study area (b), and ADP (c) and RBR (d) for current and wave measurements, respectively. S1–S4 represent the four stations set up at the field site for measuring wave and current parameters.
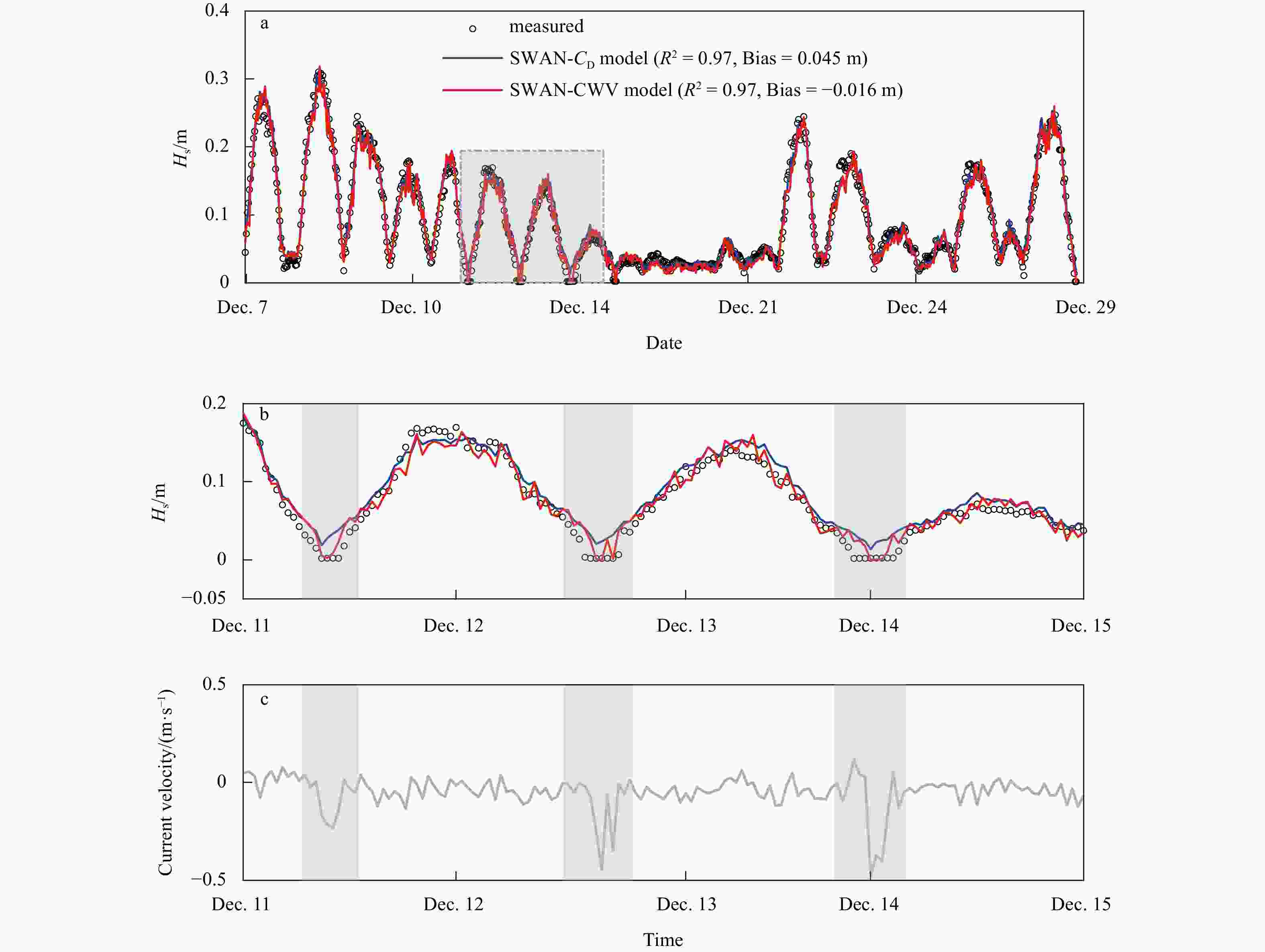
Figure 6. Comparisons between measured significant wave height in the mature mangroves and results from SWAN-
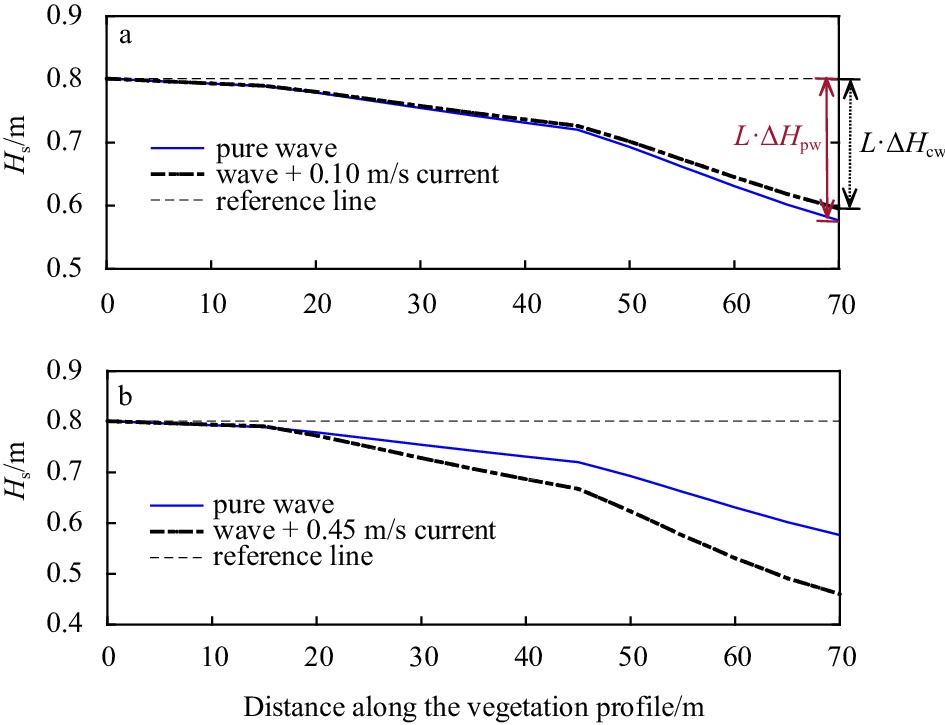
$ {C}_{\mathrm{D}} $ and SWAN-CWV models for field observations in Hailing Island (a and b), and variation of depth-averaged current velocity at Station S1 (c). The shaded area in a is enlarged in b to better show the influence of currents to wave vegetation. Three shaded parts in b represent relatively strong current in the observed period.Figure 8. Variation of the significant wave height along with the canopy in different combinations of waves and currents. a. Weak current (
$ {H}_{0} $ = 0.8 m,$ {T}_{\mathrm{p}} $ = 4.0 s,$ {U}_{\mathrm{c}} $ = 0.10 m/s); b. strong current ($ {H}_{0} $ = 0.8 m,$ {T}_{\mathrm{p}} $ = 4.0 s,$ {U}_{\mathrm{c}} $ = 0.45 m/s). The numerical test in pure wave conditions with the same incident waves was carried out as a reference to assess the currents to wave attenuation (blue line). L is the length of the vegetated area.$ \Delta {H}_{\mathrm{p}\mathrm{w}} $ and$ \Delta {H}_{\mathrm{c}\mathrm{w}} $ stand for the wave height attenuation induced by a unit length of canopies for pure wave and combined current-wave flows in Eq. (28).Figure 9. Variation of
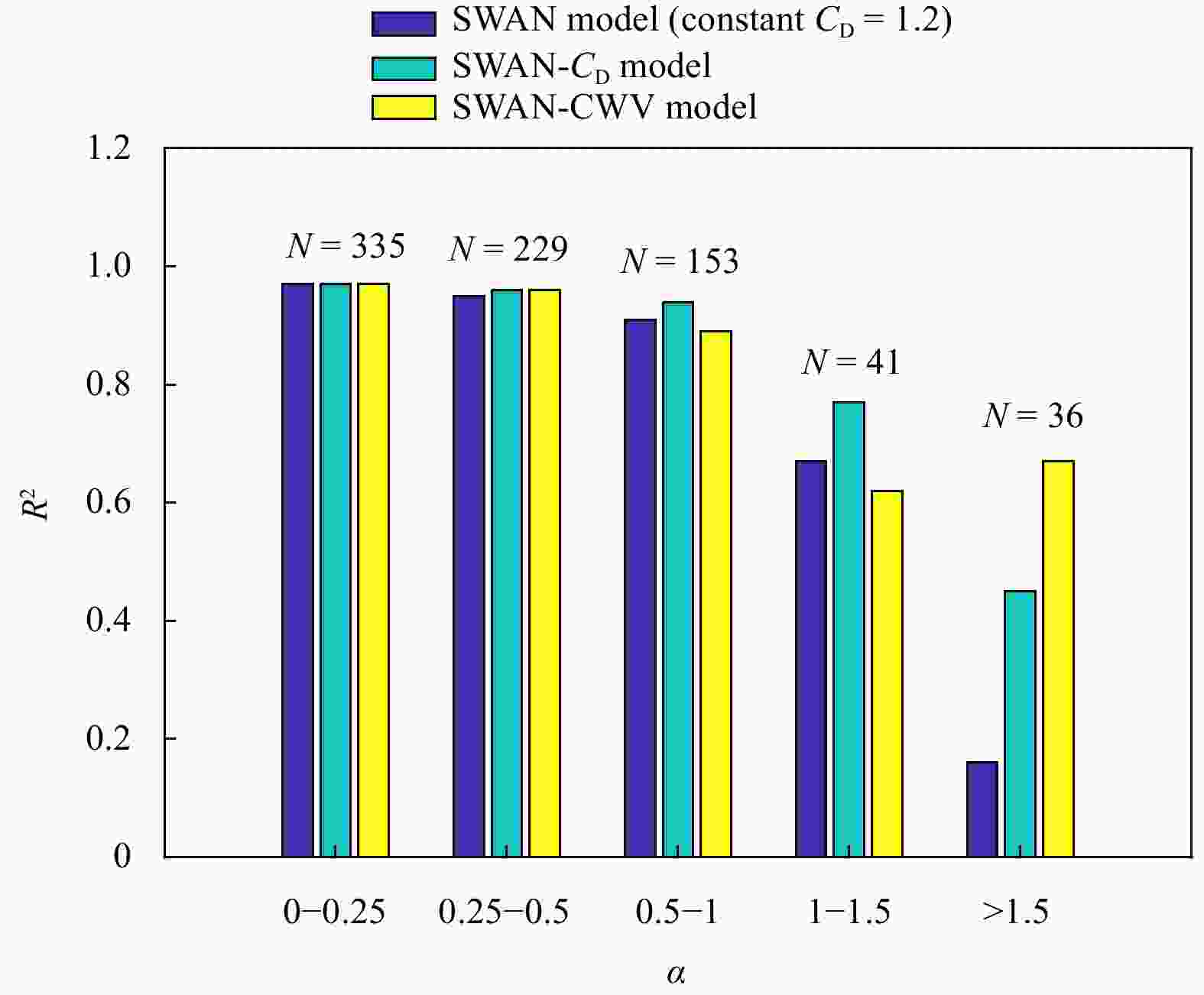
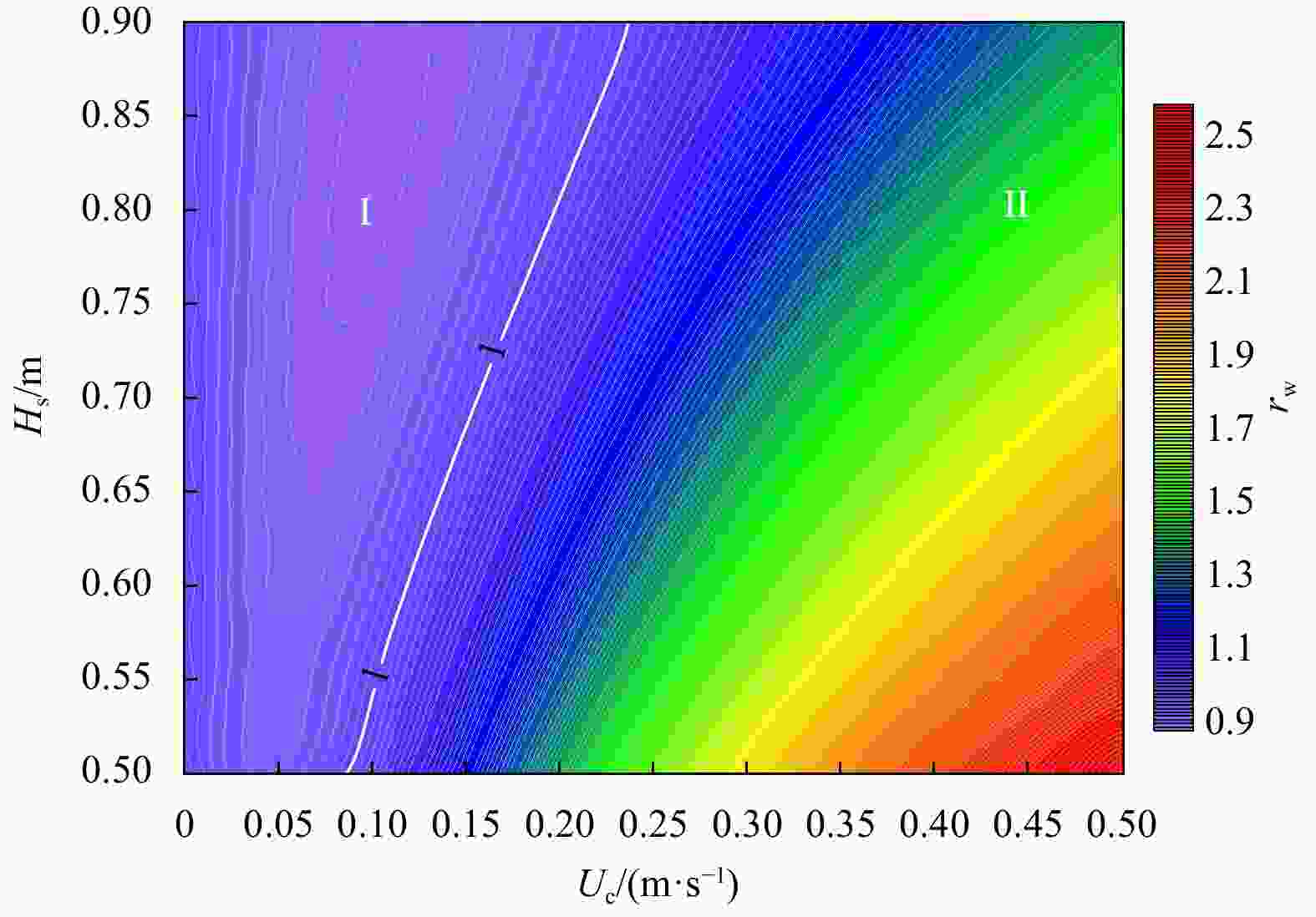
$ {r}_{\mathrm{w}} $ ($ {r}_{\mathrm{w}}=\Delta {H}_{\mathrm{c}\mathrm{w}}/\Delta {H}_{\mathrm{p}\mathrm{w}} $ ) with different hydrodynamic combinations under the storm surge. The white solid line represents contour 1 ($ {r}_{\mathrm{w}}=1 $ ), indicating that the wave attenuation caused by vegetation has neither increased nor decreased in the combined current-wave flows compared to the pure wave conditions. Area I indicates a decrease in the amount of vegetation-induced wave height reduction. Area II indicates an increase in wave attenuation by vegetation when the currents become stronger under the same wave conditions.Table 1. Input parameters of vegetation characters
Region Vegetation character Length (x)/m Height ($ {h}_{\mathrm{v}} $)/m Diameter ($ {b}_{\mathrm{v}} $)/m Density ($ {N}_{\mathrm{v}} $)/(stem·m−2) Drag coefficient ($ {C}_{\mathrm{D}} $) Mudflat 15 0 0 0 0 Seedling zone 35 0.6 0.05 6 Re-$ {C}_{\mathrm{D}} $ Mature mangrove 20 1.8 0.15 2 Re-$ {C}_{\mathrm{D}} $ -
Baron-Hyppolite C, Lashley C H, Garzon J, et al. 2019. Comparison of implicit and explicit vegetation representations in SWAN hindcasting wave dissipation by coastal wetlands in Chesapeake Bay. Geosciences, 9(1): 8. doi: 10.3390/geosciences9010008 Cao Haijin, Feng Weibing, Hu Zhan, et al. 2015. Numerical modeling of vegetation-induced dissipation using an extended mild-slope equation. Ocean Engineering, 110: 258–269. doi: 10.1016/j.oceaneng.2015.09.057 Chen Ming, Lou Sha, Liu Shuguang, et al. 2020. Velocity and turbulence affected by submerged rigid vegetation under waves, currents and combined wave-current flows. Coastal Engineering, 159: 103727. doi: 10.1016/j.coastaleng.2020.103727 Chen Hui, Ni Yan, Li Yulong, et al. 2018. Deriving vegetation drag coefficients in combined wave-current flows by calibration and direct measurement methods. Advances in Water Resources, 122: 217–227. doi: 10.1016/j.advwatres.2018.10.008 Dai Zhijun, Ge Zhenming. 2022. Research and Practice of Green Ecological Coastal Defense. Beijing: Science Press, 104–130 Dalrymple R A, Kirby J T, Hwang P A. 1984. Wave diffraction due to areas of energy dissipation. Journal of Waterway, Port, Coastal, and Ocean Engineering, 110(1): 67–79 De Dominicis M, Wolf J, van Hespen R, et al. 2023. Mangrove forests can be an effective coastal defence in the Pearl River Delta, China. Communications Earth & Environment, 4(1): 13. doi: 10.1038/s43247-022-00672-7 Garzon J L, Maza M, Ferreira C M, et al. 2019. Wave attenuation by Spartina saltmarshes in the Chesapeake Bay under storm surge conditions. Journal of Geophysical Research: Oceans, 124(7): 5220–5243. doi: 10.1029/2018JC014865 Hoque A, Husrin S, Oumeraci H. 2018. Laboratory studies of wave attenuation by coastal forest under storm surge. Coastal Engineering Journal, 60(2): 225–238. doi: 10.1080/21664250.2018.1486268 Hu Zhan, Lian Simei, Wei Huaiyu, et al. 2021. Laboratory data on wave propagation through vegetation with following and opposing currents. Earth System Science Data, 13(10): 4987–4999. doi: 10.5194/essd-13-4987-2021 Hu Zhan, Lian Simei, Zitman T, et al. 2022. Wave breaking induced by opposing currents in submerged vegetation canopies. Water Resources Research, 58(4): e2021WR031121. doi: 10.1029/2021WR031121 Hu Zhan, Suzuki T, Zitman T, et al. 2014. Laboratory study on wave dissipation by vegetation in combined current-wave flow. Coastal Engineering, 88: 131–142. doi: 10.1016/j.coastaleng.2014.02.009 Hu Zhan, Zhou Juanling, Wang Chen, et al. 2020. A novel instrument for bed dynamics observation supports machine learning applications in mangrove biogeomorphic processes. Water Resources Research, 56(7): e2020WR027257. doi: 10.1029/2020WR027257 Hudspeth R T, Sulisz W. 1991. Stokes drift in two-dimensional wave flumes. Journal of Fluid Mechanics, 230: 209–229. doi: 10.1017/S0022112091000769 Lara J L, Maza M, Ondiviela B, et al. 2016. Large-scale 3-D experiments of wave and current interaction with real vegetation. Part 1: Guidelines for physical modeling. Coastal Engineering, 107: 70–83. doi: 10.1016/j.coastaleng.2015.09.012 Li C W, Yan K. 2007. Numerical investigation of wave-current-vegetation interaction. Journal of Hydraulic Engineering, 133(7): 794–803. doi: 10.1061/(ASCE)0733-9429(2007)133:7(794 Loder N M, Irish J L, Cialone M A G, et al. 2009. Sensitivity of hurricane surge to morphological parameters of coastal wetlands. Estuarine, Coastal and Shelf Science, 84(4): 625–636 Longuet-Higgins M S, Stewart R W. 1960. Changes in the form of short gravity waves on long waves and tidal currents. Journal of Fluid Mechanics, 8(4): 565–583. doi: 10.1017/S0022112060000803 Longuet-Higgins M S, Stewart R W. 1961. The changes in amplitude of short gravity waves on steady non-uniform currents. Journal of Fluid Mechanics, 10(4): 529–549. doi: 10.1017/S0022112061000342 Losada I J, Maza M, Lara J L. 2016. A new formulation for vegetation-induced damping under combined waves and currents. Coastal Engineering, 107: 1–13. doi: 10.1016/j.coastaleng.2015.09.011 Maza M, Lara J L, Losada I J, et al. 2015. Large-scale 3-D experiments of wave and current interaction with real vegetation. Part 2: Experimental analysis. Coastal Engineering, 106: 73–86. doi: 10.1016/j.coastaleng.2015.09.010 Mendez F J, Losada I J. 2004. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coastal Engineering, 51(2): 103–118. doi: 10.1016/j.coastaleng.2003.11.003 Möller I, Kudella M, Rupprecht F, et al. 2014. Wave attenuation over coastal salt marshes under storm surge conditions. Nature Geoscience, 7(10): 727–731. doi: 10.1038/NGEO2251 Morison J R, Johnson J W, Schaaf S A. 1950. The force exerted by surface waves on piles. Journal of Petroleum Technology, 2(5): 149–154. doi: 10.2118/950149-g Neumann J E, Emanuel K A, Ravela S, et al. 2015. Risks of coastal storm surge and the effect of sea level rise in the Red River Delta, Vietnam. Sustainability, 7(6): 6553–6572. doi: 10.3390/su7066553 Ota T, Kobayashi N, Kirby J T. 2004. Wave and current interactions with vegetation. In: Coastal Engineering 2004. Lisbon, Portugal: World Scientific, 508–520, Paul M, Bouma T J, Amos C L. 2012. Wave attenuation by submerged vegetation: Combining the effect of organism traits and tidal current. Marine Ecology Progress Series, 444: 31–41. doi: 10.3354/meps09489 Rupprecht F, Möller I, Paul M, et al. 2017. Vegetation-wave interactions in salt marshes under storm surge conditions. Ecological Engineering, 100: 301–315. doi: 10.1016/j.ecoleng.2016.12.030 Sheng Y P, Lapetina A, Ma Gangfeng. 2012. The reduction of storm surge by vegetation canopies: Three-dimensional simulations. Geophysical Research Letters, 39(20): L20601. doi: 10.1029/2012GL053577 Suzuki T, Zijlema M, Burger B, et al. 2012. Wave dissipation by vegetation with layer schematization in SWAN. Coastal Engineering, 59(1): 64–71. doi: 10.1016/j.coastaleng.2011.07.006 Tanaka N. 2009. Vegetation bioshields for tsunami mitigation: review of effectiveness, limitations, construction, and sustainable management. Landscape and Ecological Engineering, 5(1): 71–79. doi: 10.1007/s11355-008-0058-z Tanaka N, Jinadasa K B S N, Mowjood M I M, et al. 2011. Coastal vegetation planting projects for tsunami disaster mitigation: effectiveness evaluation of new establishments. Landscape and Ecological Engineering, 7(1): 127–135. doi: 10.1007/s11355-010-0122-3 Temmerman S, Meire P, Bouma T J, et al. 2013. Ecosystem-based coastal defence in the face of global change. Nature, 504(7478): 79–83. doi: 10.1038/nature12859 The WAMDI Group. 1988. The WAM model—A third generation ocean wave prediction model. Journal of Physical Oceanography, 18(12): 1775–1810. doi: 10.1175/1520-0485(1988)018<1775:TWMTGO>2.0.CO;2 Vandenbruwaene W, Temmerman S, Bouma T J, et al. 2011. Flow interaction with dynamic vegetation patches: Implications for biogeomorphic evolution of a tidal landscape. Journal of Geophysical Research: Earth Surface, 116(F1): F01008. doi: 10.1029/2010JF001788 van Loon-Steensma J M, Hu Zhan, Slim P A. 2016. Modelled impact of vegetation heterogeneity and salt-marsh zonation on wave damping. Journal of Coastal Research, 32(2): 241–252. doi: 10.2112/JCOASTRES-D-15-00095.1 van Loon-Steensma J M, Slim P A, Decuyper M, et al. 2014. Salt-marsh erosion and restoration in relation to flood protection on the Wadden Sea barrier island Terschelling. Journal of Coastal Conservation, 18(4): 415–430. doi: 10.1007/s11852-014-0326-z Vuik V, Jonkman S N, Borsje B W, et al. 2016. Nature-based flood protection: The efficiency of vegetated foreshores for reducing wave loads on coastal dikes. Coastal Engineering, 116: 42–56. doi: 10.1016/j.coastaleng.2016.06.001 Wang Jun, Yi Si, Li Mengya, et al. 2018. Effects of sea level rise, land subsidence, bathymetric change and typhoon tracks on storm flooding in the coastal areas of Shanghai. Science of the Total Environment, 621: 228–234. doi: 10.1016/j.scitotenv.2017.11.224 Wu Weicheng, Ma Gangfeng, Cox D T. 2016. Modeling wave attenuation induced by the vertical density variations of vegetation. Coastal Engineering, 112: 17–27. doi: 10.1016/j.coastaleng.2016.02.004 Yang Yongqian, Irish J L. 2018. Evolution of wave spectra in mound-channel wetland systems. Estuarine, Coastal and Shelf Science, 207: 444–456, Yang Yongqian, Irish J L, Socolofsky S A. 2015. Numerical investigation of wave-induced flow in mound-channel wetland systems. Coastal Engineering, 102: 1–12. doi: 10.1016/j.coastaleng.2015.05.002 Yin Zegao, Wang Yanxu, Liu Yong, et al. 2020. Wave attenuation by rigid emergent vegetation under combined wave and current flows. Ocean Engineering, 213: 107632. doi: 10.1016/j.oceaneng.2020.107632 Zainali A, Marivela R, Weiss R, et al. 2018. Numerical simulation of nonlinear long waves in the presence of discontinuous coastal vegetation. Marine Geology, 396: 142–149. doi: 10.1016/j.margeo.2017.08.001 Zhang Wei, Ge Zhenming, Li Shihua, et al. 2022. The role of seasonal vegetation properties in determining the wave attenuation capacity of coastal marshes: implications for building natural defenses. Ecological Engineering, 175: 106494. doi: 10.1016/j.ecoleng.2021.106494 Zhang Xiaoxia, Lin Pengzhi, Nepf H. 2021. A simple-wave damping model for flexible marsh plants. Limnology and Oceanography, 66(12): 4182–4196. doi: 10.1002/lno.11952 Zhang Xiaoxia, Nepf H. 2021. Wave damping by flexible marsh plants influenced by current. Physical Review Fluids, 6(10): 100502. doi: 10.1103/PhysRevFluids.6.100502 Zhao Haihong, Chen Qin. 2014. Modeling attenuation of storm surge over deformable vegetation: methodology and verification. Journal of Engineering Mechanics, 140(12): 04014090. doi: 10.1061/(ASCE)EM.1943-7889.0000704 Zhao Chuyan, Tang Jun, Shen Yongming, et al. 2021. Study on wave attenuation in following and opposing currents due to rigid vegetation. Ocean Engineering, 236: 109574. doi: 10.1016/j.oceaneng.2021.109574 Zhao Chuyan, Zhang Yan, Tang Jun, et al. 2020. Numerical investigation of solitary wave run-up attenuation by patchy vegetation. Acta Oceanologica Sinica, 39(5): 105–114. doi: 10.1007/s13131-020-1572-6 Zhou Xiaoyan, Dai Zhijun, Pang Wenhong, et al. 2022. Wave attenuation over mangroves in the Nanliu Delta, China. Frontiers in Marine Science, 9: 874818. doi: 10.3389/fmars.2022.874818 Zheng Jinhai, Xu Wei, Tao Aifeng, et al. 2023. Synergy between coastal ecology and disaster mitigation in China: Policies, practices, and prospects. Ocean & Coastal Management, 245: 106866. doi: https://doi.org/10.1016/j.ocecoaman.2023.106866 -





 下载:
下载: