Forty-year investigation of wave power in energetic region of Persian Gulf in Iranian territorial waters by using short-term and new long-term stability assessment parameters
-
Abstract: The wave power in high potential area of the northern Persian Gulf (near to Iranian coastal areas) is assessed by taking into account the temporal and spatial distributions of wave power for a period of forty years. For this purpose, assimilated wind data of European Centre for Medium-Range Weather Forecasting Interim Reanalysis (ERA-Interim), and hydrography data of General Bathymetric Chat of the oceans (GEBCO) are used as SWAN model. Seven locations are investigated in the study area by considering the amount of coefficient of variation, the amount of average annual power, and the short-term and a new long-term (decadal variability index) power stability assessment parameters. The results showed more stability in the eastern parts of the study area and concluded that a narrow line between the point which is in the middle and another point which is in the eastern middle part of the study area may be the best locations for more investigation and the feasibility study for energy converter farms. Also, it is found that the middle part of the study region with about 2.5 kW/m power is the most energetic area. It is concluded that the dominant direction of wave power distribution in all points is the northeast, and this dominant direction has not changed during the forty-year period. It is observed that the mean annual energy increases with a slight slope in the total 40 a, and this increasing trend is more obvious in the fourth decade. Although it is observed that the wave power of the second decade has the most stability and the least variation, the wave power in the fourth decade has the most variation. Moreover, the results showed that the study region’s wave power increase by approximately a mean change rate of 0.027 kW/(m·a); and the maximum change rate of wave power was in the northwest part and the minimum change rate of wave power was in the southeast part which were about 0.036 kW/(m·a) and 0.014 kW/(m·a), respectively.
-
Key words:
- wave energy /
- SWAN model /
- wind assimilated data /
- Persian Gulf /
- numerical modeling /
- decadal assessment
-
1. Introduction
Today, the study and exploitation of renewable energy are very important subjects, because such energy is clean and can be used permanently. In this regard, many studies have been conducted in recent years.
Some researchers investigated different areas for the wave energy extraction such as the Black Sea (Akpınar and Kömürcü, 2013), Marmara Sea (Kutupoğlu et al., 2018), Caspian Sea (Kamranzad et al., 2016b), South China Sea (Wan et al., 2015, Mirzaei et al., 2015), East China Sea (Wu et al., 2015), the northwest European shelf seas (Neill and Hashemi, 2013), Galway Bay (Rute Bento et al., 2015), the nearshore shelf waters off Australia (Morim et al., 2014), Caribbean Sea (Ortega et al., 2013), Anzali Port (Hadadpour et al., 2014), global oceanic with the Maritime Silk Road as a case study (Zheng, 2021), global ocean (Zheng et al., 2014), and the seas around Australia, Indonesia, northern Spain and China (Hughes and Heap, 2010, Amiruddin et al., 2019, Rute Bento et al., 2018, Zheng and Li, 2015). In other studies, Kamranzad et al. (2016a) and Saket and Etemad-Shahidi (2012) also studied the energy of waves in the Oman Sea.
Moreover, the potential for wind and wave energy extraction in different areas is investigated by Langodan et al. (2016), Wang et al. (2016) and Rusu and Onea (2013).
In another study, the North Scottish area has been investigated, which is one of the most suitable areas for wave and tidal energy exploitation. In this area, there have been a lot of energy extraction economic sites in the past, and this has led to a small amount of data and results. After using 10 a wind field data (between 2003 and 2012) and SWAN numerical model, it was found that during December and March, there were many changes in the amount of energy which were between 10 kW/m and 25 kW/m (Neill et al., 2014).
The feasibility using waves and tidal energy of the Iranian seas was also investigated in order to determine the best points for extracting marine energy in these areas. The results showed that the Qeshm Canal is a suitable area for tidal energy extraction (Soleimani et al., 2015).
In another study, the energy of the Persian Gulf area was also studied for a 25-a period (since 1984 to 2008) and it was shown that the middle part of the Persian Gulf is its energetic part (Kamranzad et al., 2013).
2. Computational method
The Persian Gulf is a semi-closed aqueous area where Iran is located on its north margin and Arabic countries are in the south part of this area. This gulf is connected to the Oman Sea by the Hormuz Strait, which is fed by direct contact with the Indian Ocean. The gulf has a mean depth of 36 m, where it is rarely found to be above 90 m. The deeper part of the Persian Gulf is in its northern area and near its Iranian shores. Since the Persian Gulf area is a strategic and important area economically, politically and militarily and it is an important and well-known crossing point for the transfer of goods and fuel, there is a great need for energy in this area (Kamranzad et al., 2013).
2.1 Numerical modeling
The specifications of waves were obtained from SWAN numerical model, which is a third-generation all-spectral wave model. This model has been used in the past to study this area, which has provided results with acceptable accuracy. SWAN numerical model is based more on the spectrum density of the operator N (σ, θ) than on the energy density E (σ, θ), because the operator density is constant in the presence of current, while the energy density is not constant. The operator density is defined as follows:
$$ N(\sigma, \theta)= E(\sigma,\theta)/\sigma , $$ (1) where θ is the wave propagation direction, and σ is the relative angular frequency.
2.2 Data sources
The hydrography data of the study area were obtained from GEBCO, which has the grid distance of 30 s (approximately 835 m). Also, the assimilated wind field data which obtained from European Centre for Medium-Range Weather Forecasting have been used as model inputs at intervals of 6 h and spatial distances of 0.75° that were interpolated as a grid with spatial distances of 0.125° for a period of 40 a (since 1979 to 2018).
2.3 Model sensitivity analysis
In order to assess the impact of the water level, computational space-grid time steps, and computational space-grid intervals changes on the waves’ characteristics such as Hs (significant wave height) and Tp (peak period), a point with coordinates of (26.2°N, 56°E) was used for sensitivity analysis.
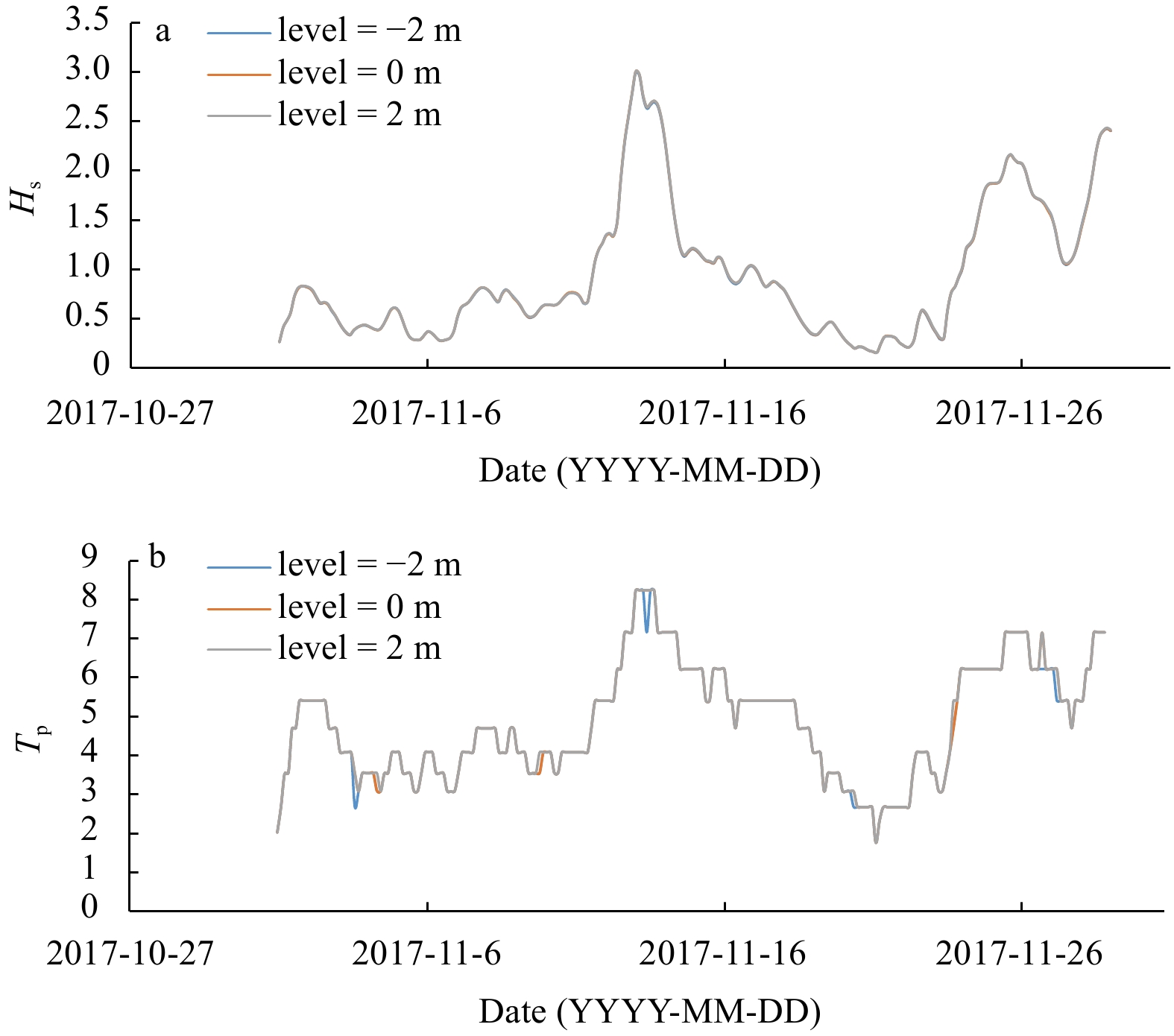
The water level was assessed by using the SWAN model with three types of water levels (+2 m, 0 m, and –2 m). It should be noted that the average tidal range in Persian Gulf is between l m to 2 m (Lambeck, 1996). The results which are shown in Fig. 1 illustrate that the water level changes don’t have any special impact on the significant wave height and wave period parameters.
Also, in order to investigate the impact of the computational time steps on the waves’ characteristics, the time steps of 300 s, 600 s, and 1200 s are used. Figure 2 can be seen that there is a good agreement between all of the studied time steps.
Finally, in order to investigate the impact of the computational space-grid intervals on the waves’ characteristics, the intervals of 0.5°, 0.2°, 0.1°, and 0.05° are used. By considering the results, Fig. 3 can be concluded that there is a good agreement between all of the studied space-grid intervals.
Therefore, it can be concluded that the water level of 0 m, the computational space-grid time steps of 600 s, and the space-grid intervals of 0.1° are strictly suitable for SWAN model in the Persian Gulf.
2.4 Model validation
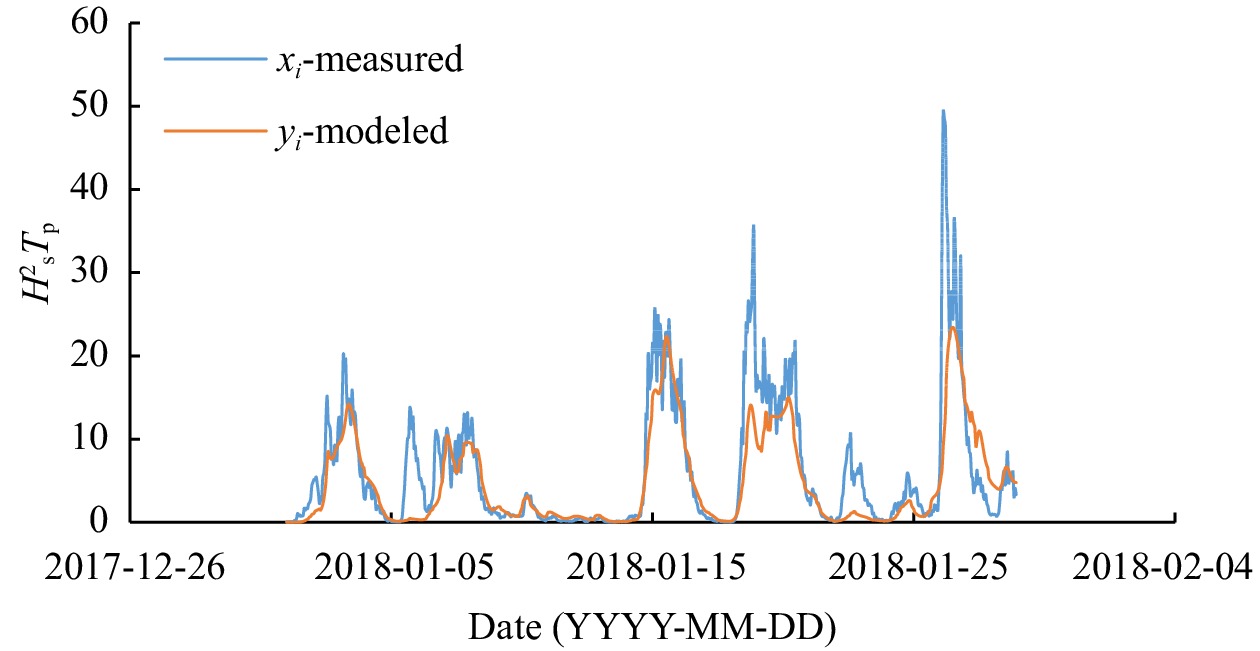
The results obtained from the model were calibrated by two buoys for recording data, one near Kish Island and the other near Bushehr Port, and then verified. In order to calibrate the results, the buoy data related to December 2017 have been used, and in order to verify the results, the January 2018 buoy data have been used. It should be noted that the model was calibrated based on wave energy parameters so that according to the main objective of the study, the accuracy of the obtained outputs would be higher.
In order to ensure the accuracy of the model, error indices such as bias, correlation coefficient (CC), root mean square error (RMSE), and scatter index (SI) were used. The equations related to the above indices are as follows:
$$ {\rm{Bias}}=\bar{y}-\bar{x} .$$ (2) $$ {\rm{CC}}=\frac{\displaystyle\sum _{i}\left(\left({x}_{i}-\bar{x}\right)\times \left({y}_{i}-\bar{y}\right)\right)}{\sqrt{\displaystyle\sum _{i}{\left({x}_{i}-\bar{x}\right)}^{2}\sum _{i}{\left({y}_{i}-\bar{y}\right)}^{2}}}. $$ (3) $$ {\rm{RMSE}}=\sqrt{\frac{\displaystyle\sum _{i}{({x}_{i}-{y}_{i})}^{2}}{n}} .$$ (4) $$ {\rm{SI}}=\frac{{\rm{RMSE}}}{\bar{x}} . $$ (5) In Eqs (2)−(5),
$ {x}_{i} $ and$ {y}_{i} $ are the actual and modeled measured values, respectively, and$ \bar{x} $ and$ \bar{y} $ are their mean values (Kamranzad et al., 2013).The wave specifications of model output were obtained at temporal and spatial intervals of 1 h and 0.1°, respectively. In Figs 4 and 5, the time series of the
${H}_{{\rm{s}}}^{2}{T}_{{\rm{P}}}$ parameter for Bushehr and Kish are shown, respectively. The model has shown appropriate accuracy. Error indices are also shown in Tables 1 and 2 to ensure that the model’s accuracy is acceptable.Table 1. Statistical parameters of Bushehr buoy errorBushehr Bias RMSE SI CC Hs 0.12 0.34 0.36 0.84 Tp 0.03 0.79 0.18 0.78 Hs2Tp 1.41 4.74 0.77 0.82 Note: CC: correlation coefficient; RMSE: root mean square error; SI: scatter index. Hs: significant wave height; Tp: peak wave period. Table 2. Statistical parameters of Kish buoy errorKish Bias RMSE SI CC Hs 0.1 0.23 0.36 0.9 Tp 0.24 0.55 0.16 0.84 Hs2Tp 0.43 2.28 0.84 0.87 Note: CC: correlation coefficient; RMSE: root mean square error; SI: scatter index. Hs: significant wave height; Tp: the peak wave period. 2.5 Estimation of wave energy
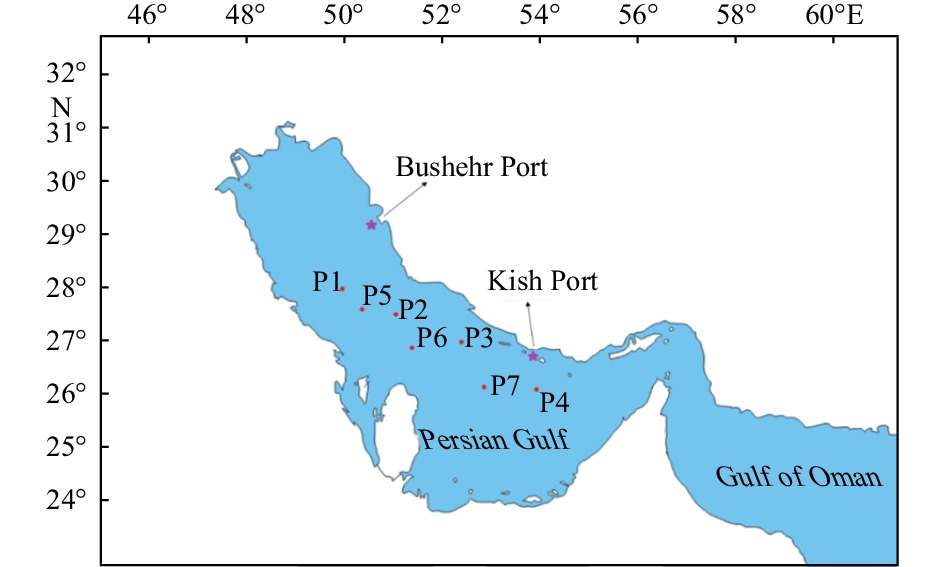
This study has investigated the decadal wave energy in the energetic area of the Persian Gulf. For this purpose, 7 points in the mentioned area have been investigated, whose locations are shown in Fig. 6. The wave energy is calculated based on the following equation:
$$ E=\frac{1}{16}\rho g{H}_{{\rm{s}}}^{2} , $$ (6) where
$ \rho $ , g, and${H}_{{\rm{s}}}$ represent the density of seawater, gravity acceleration, and significant wave height, respectively (Kamranzad et al., 2013).The wave energy flux (wave power, P ) is also obtained using the following equation:
$$ P=E{C}_{g}=ECn , $$ (7) where C is the wave velocity; n represents the ratio of the wave group velocity to the wave velocity, which in deep water is approximately 0.5. Also, C is obtained by dividing the wave length by the wave period (Kamranzad et al., 2013). Therefore, the wave power can be estimated using Eq. (8):
$$ P=\frac{1}{16}\rho g{H}_{{\rm{s}}}^{2}\frac{gT}{2\pi }\times 0.5 \simeq 0.49{H}_{{\rm{s}}}^{2}{T}_{{\rm{e}}}, $$ (8) where
${T}_{{\rm{e}}}$ in the above equation is the wave period obtained from multiplying${T}_{{\rm{P}}}$ by a coefficient, which is 0.9 for Jonswap wave spectrum (Abbaspour and Rahimi, 2011).The real waves in the sea are obtained from combining a large number of regular waves. Therefore, the wave power per unit width for irregular waves is obtained using Eq. (9):
$$ P=0.49{H}_{{\rm{s}}}^{2}{T}_{{\rm{e}}} . $$ (9) 3. Results and discussion
3.1 Mean total and annual wave power assessment
The specifications of wind waves were extracted in energetic areas of the Persian Gulf for a period of 40 a (1979–2018). In Table 3 and Fig. 7, the mean decadal energy in 7 points under investigation is given. It is observed that Points 2, 6 and 7 have the highest mean energy, with Point 6 having the highest value among them.
Table 3. Mean energy in 4 decades at the study pointsPoint 1 Point 2 Point 3 Point 4 Point 5 Point 6 Point 7 Total average
power/(kW·m−1)2.01 2.43 2.00 2.01 2.28 2.52 2.50 The mean annual energy was evaluated in all points in four different decades. As shown in Fig. 8, although the second decade has the lowest mean changes in energy in the studied years, on the contrary, the first and fourth decades have high mean annual changes in all points and this is cause of the differences between the mean wind speed in the second decade years compare to the other decades years. The third decade, after the second decade, is a relatively stable decade in which from the beginning to the end, the mean annual energy increases with a slight slope and change. It is also observed that the mean annual energy increases with a slight slope in the total 40 a. This increasing trend is more obvious in the fourth decade and this decade has the highest mean energy in comparison with other decades in all points. The results showed that the study region’s wave power increase by approximately a mean change rate of 0.027 kW/(m·a). The maximum change rate of wave power was in Point 2 and the minimum change rate of wave power was in Point 4 which were about 0.036 kW/(m·a) and 0.014 kW/(m·a) respectively. Also, it can be seen that year 2017 has the most energy in all of the points compared to the other years. Moreover, the middle points (Points 2, 6 and 7) are more energetic than the other points.
3.2 Wave power direction
Estimating the dominant direction of the wave energy is very important in the discussion of the use of energy converters, so in Fig. 9 to Fig. 11, the energy of the waves at Points 1, 4 and 6, which are investigated in the west, east and center parts of the area under study, respectively, are shown in four different decades on behalf of all points. As shown in Fig. 9 to Fig. 11, by moving from west to east in the energetic area of the Persian Gulf, the direction of energy and power of the waves gradually change from north-south to west-east. Also, it is clear that the dominant direction of the waves is to the southeast which is due to the Shamal wind, which blows from the northwest to the southeast in the Persian Gulf region (Mahmoodi et al., 2019). The dominant direction of the waves and their energy have been stable over the decades which is due to the wind direction stability. It can also be seen that as we move from the first decade to the fourth decade, the power of the wave increases in the dominant direction, indicating that the waves become more energetic over time.
3.3 Short-term and new long-term stability assessment parameters
The Cv parameter, which is the wave power coefficient of variation, shows the stability of wave energy in different months. The calculation method of this parameter is as follows:
$$ C_{\rm{v}}=\frac{S}{\bar{x}} , $$ (10) where Cv is the coefficient of variation,
$\bar{x}$ is the mean value, and S is the standard deviation.Moreover, the standard deviation can be calculated by Eq. (11):
$$ S=\sqrt{\frac{\displaystyle\sum _{i}{{x}_{i}}^{2}-\left(\sum _{i}{x}_{i}\right)^{2}/n}{n-1}}. $$ (11) The smaller amount of Cv shows more stability in wave energy (Zheng et al., 2013). The amount of Cv for every points in all months are shown in Fig. 12.
As it can be seen in Fig. 12, in all studied points, the Cv parameter is lower in June than the other months and it shows more stability in this month than the others. This figure shows less oscillation for different months and also less amount of average Cv in Point 4, which is in the eastern part of the study area in spite of the fact that in Points 1 and 5, which are in the western part, the result is vice versa. Therefore, it can be concluded that the eastern part of the study area is more stable than the other parts.
Also, the amount of average annual power (MVI) (and short-term power (SVI)) which are the ratio of the difference between the maximum and minimum monthly (and seasonal) mean wave power and the annual mean wave power parameters for the studied points are shown in Table 4. These parameters are used for stability evaluation of the seasonal and monthly wave powers and to determine the temporal variability of the wave power (Kamranzad et al., 2016b).
Table 4. The amount of average annual power (MVI) and short term power (SVI) parameters in all studied pointsPoint number MVI SVI Point 1 1.585 1.209 Point 2 1.800 1.164 Point 3 1.556 1.027 Point 4 1.481 1.082 Point 5 1.756 1.218 Point 6 1.793 1.100 Point 7 1.215 1.045 Table 4 also shows that the energy is more stable in the points which are in the eastern part of the study area. This means that the energy in the eastern part of the energetic area of Persian Gulf is more predictable and the risk of using energy converter farms in this part is less than the other parts.
The MVI and SVI parameters are used only for the stability assessment in short time-limit, so for long-time assessments, a new parameter named DVI (decadal variability index) is proposed, which is the ratio of the difference between the maximum and minimum decadal mean wave power and the annual mean wave power. The values of this new parameter for the studied points are shown in Table 5.
Table 5. The decadal variability index (DVI) parameter in all studied pointsPoint Number DVI Point 1 0.429 Point 2 0.466 Point 3 0.353 Point 4 0.194 Point 5 0.468 Point 6 0.383 Point 7 0.237 As it can be seen, the DVI parameter has lower values in the eastern parts. Then, by considering the mean power amounts and the stability parameters, it can be concluded that a narrow line between Points 6 and 7 can be the best location for more investigation and feasibility study for energy converter farms in the Iranian territorial waters of the Persian Gulf.
4. Conclusions
In general, the study results showed that the middle points of the north of the Persian Gulf energetic area with about 2.5 kW/m power have the highest mean energy. It was also observed that although moving from west to east of the energetic area of the Persian Gulf, the direction of energy and power of the waves gradually changes from north-south to west-east, the dominant direction of the waves is to the southeast. The dominant direction of the waves and their power has been also stable during different decades, and by moving from the first decade to the fourth decade, the power of the waves increases in the dominant direction, which indicates that the waves become more energetic over time. It was also found that the second decade had the lowest mean energy changes in the studied years and the fourth decade had high annual mean energy changes in all points. The third decade, after the second decade, is a relatively stable decade in which from the beginning to the end, the mean annual energy increases with a slight slope and change. Also, it can be seen that the mean annual energy increases with a slight slope in the total 40 a. This increasing trend is more obvious in the fourth decade. Moreover, it was found that the study region’s wave power increase by approximately a mean change rate of 0.027 kW/(m·a), and the maximum change rate of wave power was in Point 2 and the minimum change rate of wave power was in Point 4 which were about 0.036 kW/(m·a) and 0.014 kW/(m·a), respectively. It is also observed that the year 2017 had the most energy in all of the points in comparison with other years. The MVI and SVI parameters (for short-term stability assessment) and the Cv and DVI parameters (for long-term stability assessment) showed more wave power stability in the eastern part of the energetic region of the Persian Gulf in Iranian territorial waters. Moreover, by considering the amount of mean wave power of the studied points in all years of investigation and the results of the stability parameters, it was concluded that a narrow line between Point 6 and Point 7 can be the best location for more investigation and the feasibility study for energy converter farms in the studied area.
Acknowledgements: The authors appreciate the Ports and Maritime Organization of the Islamic Republic of Iran for providing the required data. -
Table 1. Statistical parameters of Bushehr buoy error
Bushehr Bias RMSE SI CC Hs 0.12 0.34 0.36 0.84 Tp 0.03 0.79 0.18 0.78 Hs2Tp 1.41 4.74 0.77 0.82 Note: CC: correlation coefficient; RMSE: root mean square error; SI: scatter index. Hs: significant wave height; Tp: peak wave period. Table 2. Statistical parameters of Kish buoy error
Kish Bias RMSE SI CC Hs 0.1 0.23 0.36 0.9 Tp 0.24 0.55 0.16 0.84 Hs2Tp 0.43 2.28 0.84 0.87 Note: CC: correlation coefficient; RMSE: root mean square error; SI: scatter index. Hs: significant wave height; Tp: the peak wave period. Table 3. Mean energy in 4 decades at the study points
Point 1 Point 2 Point 3 Point 4 Point 5 Point 6 Point 7 Total average
power/(kW·m−1)2.01 2.43 2.00 2.01 2.28 2.52 2.50 Table 4. The amount of average annual power (MVI) and short term power (SVI) parameters in all studied points
Point number MVI SVI Point 1 1.585 1.209 Point 2 1.800 1.164 Point 3 1.556 1.027 Point 4 1.481 1.082 Point 5 1.756 1.218 Point 6 1.793 1.100 Point 7 1.215 1.045 Table 5. The decadal variability index (DVI) parameter in all studied points
Point Number DVI Point 1 0.429 Point 2 0.466 Point 3 0.353 Point 4 0.194 Point 5 0.468 Point 6 0.383 Point 7 0.237 -
Abbaspour M, Rahimi R. 2011. Iran atlas of offshore renewable energies. Renewable Energy, 36(1): 388–398. doi: 10.1016/j.renene.2010.06.051 Akpınar A, Kömürcü M İ. 2013. Assessment of wave energy resource of the Black Sea based on 15-year numerical hindcast data. Applied Energy, 101: 502–512. doi: 10.1016/j.apenergy.2012.06.005 Amiruddin, Ribal A, Khaeruddin, et al. 2019. A 10-year wave energy resource assessment and trends of Indonesia based on satellite observations. Acta Oceanologica Sinica, 38(8): 86–93. doi: 10.1007/s13131-019-1400-z Hadadpour S, Etemad-Shahidi A, Jabbari E, et al. 2014. Wave energy and hot spots in Anzali Port. Energy, 74: 529–536. doi: 10.1016/j.energy.2014.07.018 Hughes M G, Heap A D. 2010. National-scale wave energy resource assessment for Australia. Renewable Energy, 35(8): 1783–1791. doi: 10.1016/j.renene.2009.11.001 Kamranzad B, Chegini V, Etemad-Shahidi A. 2016a. Temporal-spatial variation of wave energy and nearshore hotspots in the Gulf of Oman based on locally generated wind waves. Renewable Energy, 94: 341–352. doi: 10.1016/j.renene.2016.03.084 Kamranzad B, Etemad-shahidi A, Chegini V. 2013. Assessment of wave energy variation in the Persian Gulf. Ocean Engineering, 70: 72–80. doi: 10.1016/j.oceaneng.2013.05.027 Kamranzad B, Etemad-Shahidi A, Chegini V. 2016b. Sustainability of wave energy resources in southern Caspian Sea. Energy, 97: 549–559. doi: 10.1016/j.energy.2015.11.063 Kutupoğlu V, Çakmak R E, Akpınar A, et al. 2018. Setup and evaluation of a SWAN wind wave model for the Sea of Marmara. Ocean Engineering, 165: 450–464. doi: 10.1016/j.oceaneng.2018.07.053 Lambeck K. 1996. Shoreline reconstructions for the Persian Gulf since the last glacial maximum. Earth and Planetary Science Letters, 142(1–2): 43–57 Langodan S, Viswanadhapalli Y, Dasari H P, et al. 2016. A high-resolution assessment of wind and wave energy potentials in the Red Sea. Applied Energy, 181: 244–255. doi: 10.1016/j.apenergy.2016.08.076 Mahmoodi K, Ghassemi H, Razminia A. 2019. Temporal and spatial characteristics of wave energy in the Persian Gulf based on the ERA5 reanalysis dataset. Energy, 187: 115991. doi: 10.1016/j.energy.2019.115991 Mirzaei A, Tangang F, Juneng L. 2015. Wave energy potential assessment in the central and southern regions of the South China Sea. Renewable Energy, 80: 454–470. doi: 10.1016/j.renene.2015.02.005 Morim J, Cartwright N, Etemad-Shahidi A, et al. 2014. A review of wave energy estimates for nearshore shelf waters off Australia. International Journal of Marine Energy, 7: 57–70. doi: 10.1016/j.ijome.2014.09.002 Neill S P, Hashemi M R. 2013. Wave power variability over the northwest European shelf seas. Applied Energy, 106: 31–46. doi: 10.1016/j.apenergy.2013.01.026 Neill S P, Lewis M J, Hashemi M R, et al. 2014. Inter-annual and inter-seasonal variability of the Orkney wave power resource. Applied Energy, 132: 339–348. doi: 10.1016/j.apenergy.2014.07.023 Ortega S, Osorio A F, Agudelo P. 2013. Estimation of the wave power resource in the Caribbean Sea in areas with scarce instrumentation. Case study: Isla Fuerte, Colombia. Renewable Energy, 57: 240–248. doi: 10.1016/j.renene.2012.11.038 Rusu E, Onea F. 2013. Evaluation of the wind and wave energy along the Caspian Sea. Energy, 50: 1–14. doi: 10.1016/j.energy.2012.11.044 Rute Bento A, Martinho P, Guedes Soares C. 2015. Numerical modelling of the wave energy in Galway Bay. Renewable Energy, 78: 457–466. doi: 10.1016/j.renene.2015.01.024 Rute Bento A, Martinho P, Guedes Soares C. 2018. Wave energy assessement for northern Spain from a 33-year hindcast. Renewable Energy, 127: 322–333. doi: 10.1016/j.renene.2018.04.049 Saket A, Etemad-Shahidi A. 2012. Wave energy potential along the northern coasts of the Gulf of Oman, Iran. Renewable Energy, 40(1): 90–97. doi: 10.1016/j.renene.2011.09.024 Soleimani K, Ketabdari M J, Khorasani F. 2015. Feasibility study on tidal and wave energy conversion in Iranian seas. Sustainable Energy Technologies and Assessments, 11: 77–86. doi: 10.1016/j.seta.2015.03.006 Wan Yong, Zhang Jie, Meng Junmin, et al. 2015. Exploitable wave energy assessment based on ERA-interim reanalysis data—a case study in the East China Sea and the South China Sea. Acta Oceanologica Sinica, 34(9): 143–155. doi: 10.1007/s13131-015-0641-8 Wang Zhifeng, Dong Sheng, Dong Xiangke, et al. 2016. Assessment of wind energy and wave energy resources in Weifang Sea area. International Journal of Hydrogen Energy, 41(35): 15805–15811. doi: 10.1016/j.ijhydene.2016.04.002 Wu Shuping, Liu Chuanyu, Chen Xinping. 2015. Offshore wave energy resource assessment in the East China Sea. Renewable Energy, 76: 628–636. doi: 10.1016/j.renene.2014.11.054 Zheng Chongwei. 2021. Global oceanic wave energy resource dataset—with the Maritime Silk Road as a case study. Renewable Energy, 169: 843–854. doi: 10.1016/j.renene.2021.01.058 Zheng Chongwei, Li Chongyin. 2015. Variation of the wave energy and significant wave height in the China sea and adjacent waters. Renewable and Sustainable Energy Reviews, 43: 381–387. doi: 10.1016/j.rser.2014.11.001 Zheng Chongwei, Pan Jing, Li Jiaxun. 2013. Assessing the China sea wind energy and wave energy resources from 1988 to 2009. Ocean Engineering, 65: 39–48. doi: 10.1016/j.oceaneng.2013.03.006 Zheng Chongwei, Shao Longtan, Shi Wenli, et al. 2014. An assessment of global ocean wave energy resources over the last 45 a. Acta Oceanologica Sinica, 33(1): 92–101 -




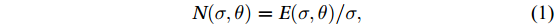

 DownLoad:
DownLoad:


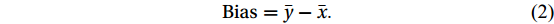
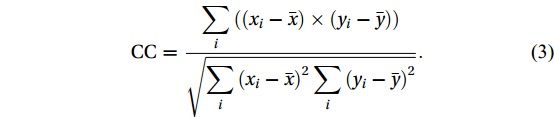
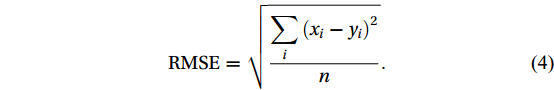

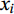
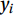
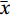

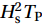

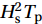

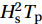
 DownLoad:
DownLoad:

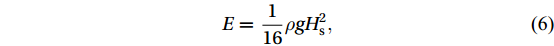
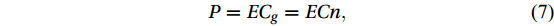
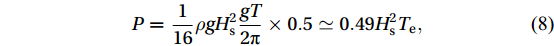
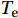
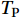
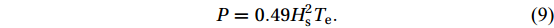





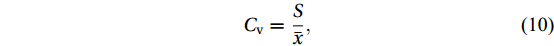



 下载:
下载: