Estimate of contribution of near-inertial waves to the velocity shear in the Bay of Bengal based on mooring observations from 2013 to 2014
-
Abstract: Near-inertial motions contribute most of the velocity shear in the upper ocean. In the Bay of Bengal (BoB), the annual-mean energy flux from the wind to near-inertial motions in the mixed layer in 2013 is dominated by tropical cyclone (TC) processes. However, due to the lack of long-term observations of velocity profiles, our knowledge about interior near-inertial waves (NIWs) as well as their shear features is limited. In this study, we quantified the contribution of NIWs to shear by integrating the wavenumber-frequency spectra estimated from velocity profiles in the upper layers (40−440 m) of the southern BoB from April 2013 to May 2014. It is shown that the annual-mean proportion of near-inertial shear out of the total is approximately 50%, and the high contribution is mainly due to the enhancement of the TC processes during which the near-inertial shear accounts for nearly 80% of the total. In the steady monsoon seasons, the near-inertial shear is dominant to or at least comparable with the subinertial shear. The contribution of NIWs to the total shear is lower during the summer monsoon than during the winter monsoon owing to more active mesoscale eddies and higher subinertial shear during the summer monsoon. The Doppler shifting of the M2 internal tide has little effect on the main results since the proportion of shear from the tidal motions is much lower than that from the near-inertial and subinertial motions.
-
Key words:
- near-inertial waves /
- shear /
- monsoon /
- tropical cyclone /
- Bay of Bengal
-
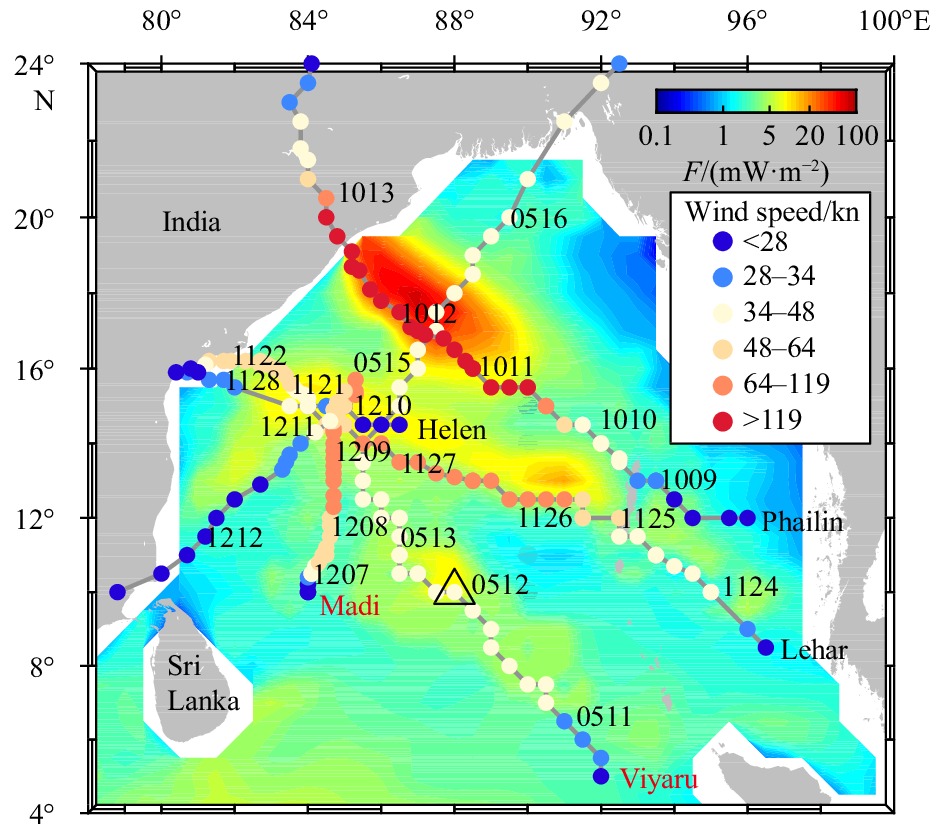
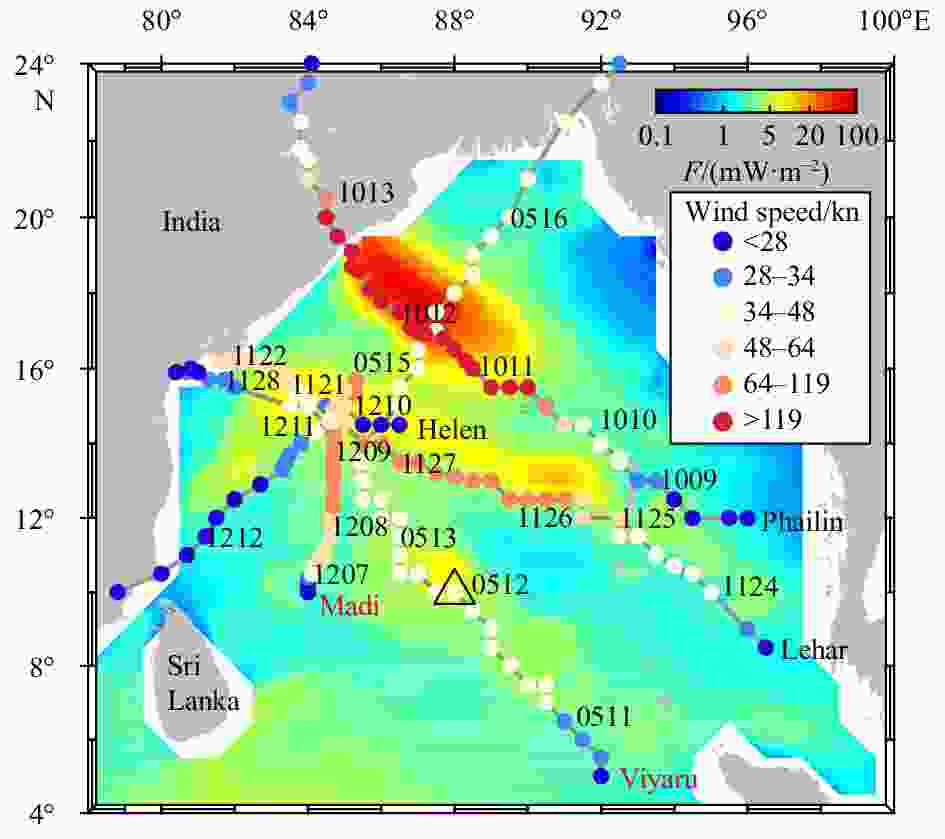
Figure 1. Distribution of annual-mean near-inertial energy flux (colors) in the BoB in 2013. The mooring location is indicated by the black triangle. Gray solid lines and color dots give the paths and strength levels of TCs in 2013, respectively. Dates (MMDD) are marked along the tracks besides the dots. The color dots represent the maximum sustained wind speed (in knots) of the TCs. The near-inertial energy flux (F) is computed by solving the Pollard-Millard slab model using the spectral method (Alford, 2003) with National Centers for Environmental Prediction (NCEP) Climate Forecast Version 2 (CSFv2) 6-hourly wind data (Saha et al., 2014) with the mixed layer depth in the slab model set to 15 m.
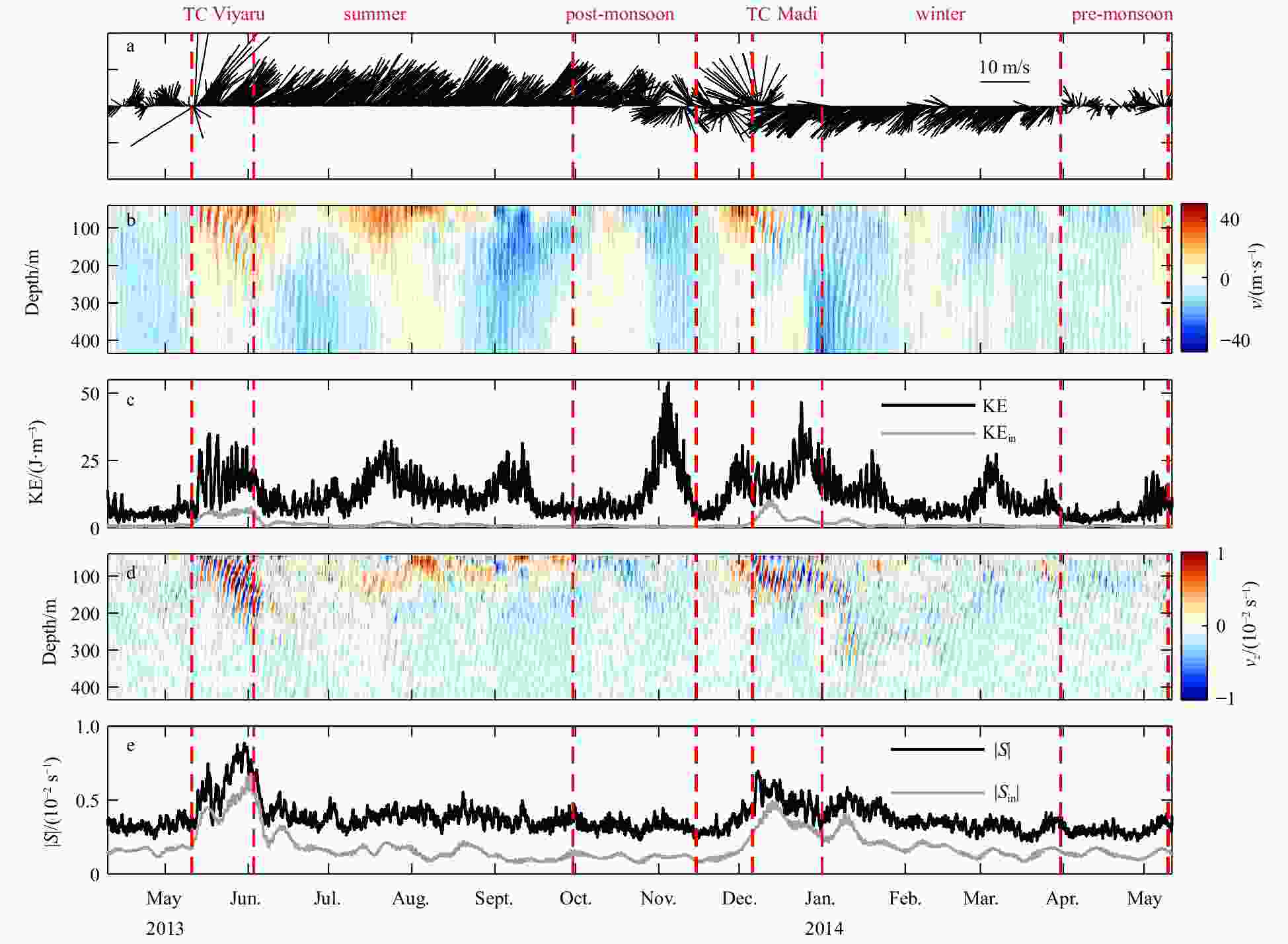
Figure 2. Mooring observations of the velocity and shear. Surface wind acquired from the NCEP CFSv2 6-hourly winds (a), observed meridional velocity (b), vertical mean of the total and near-inertial KE (c), vertical gradient of the meridional velocity (d), and vertical mean of the magnitude of the total shear and near-inertial shear (e). The red dashed lines divide the observations into six periods: TC Viyaru (May 11–June 3, 2013), summer monsoon (June–September, 2013), post-monsoon (October–mid November, 2013), TC Madi (December 6–31, 2013), winter monsoon (January–March, 2014) and pre-monsoon (April 1–May 11, 2014).
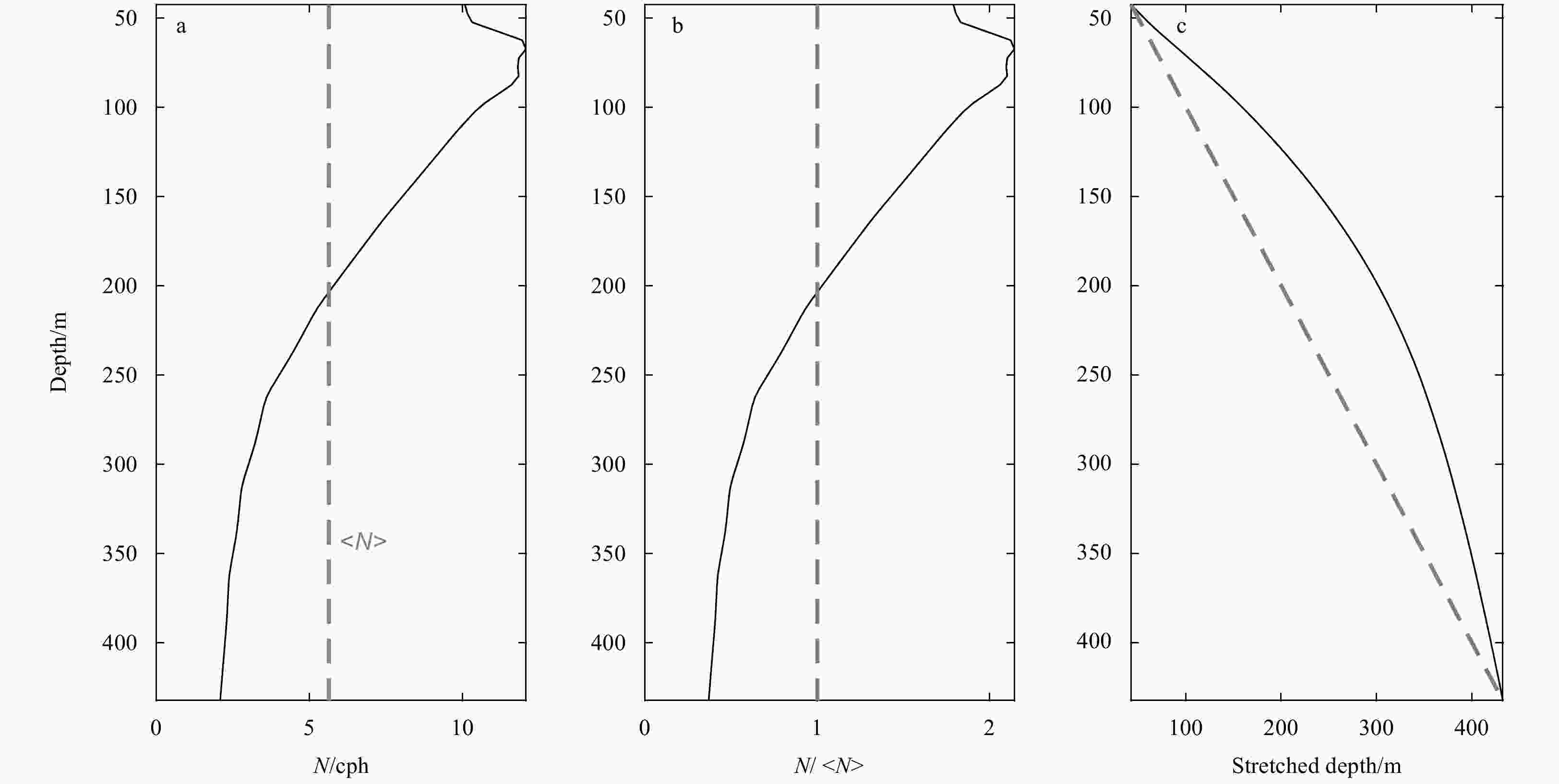
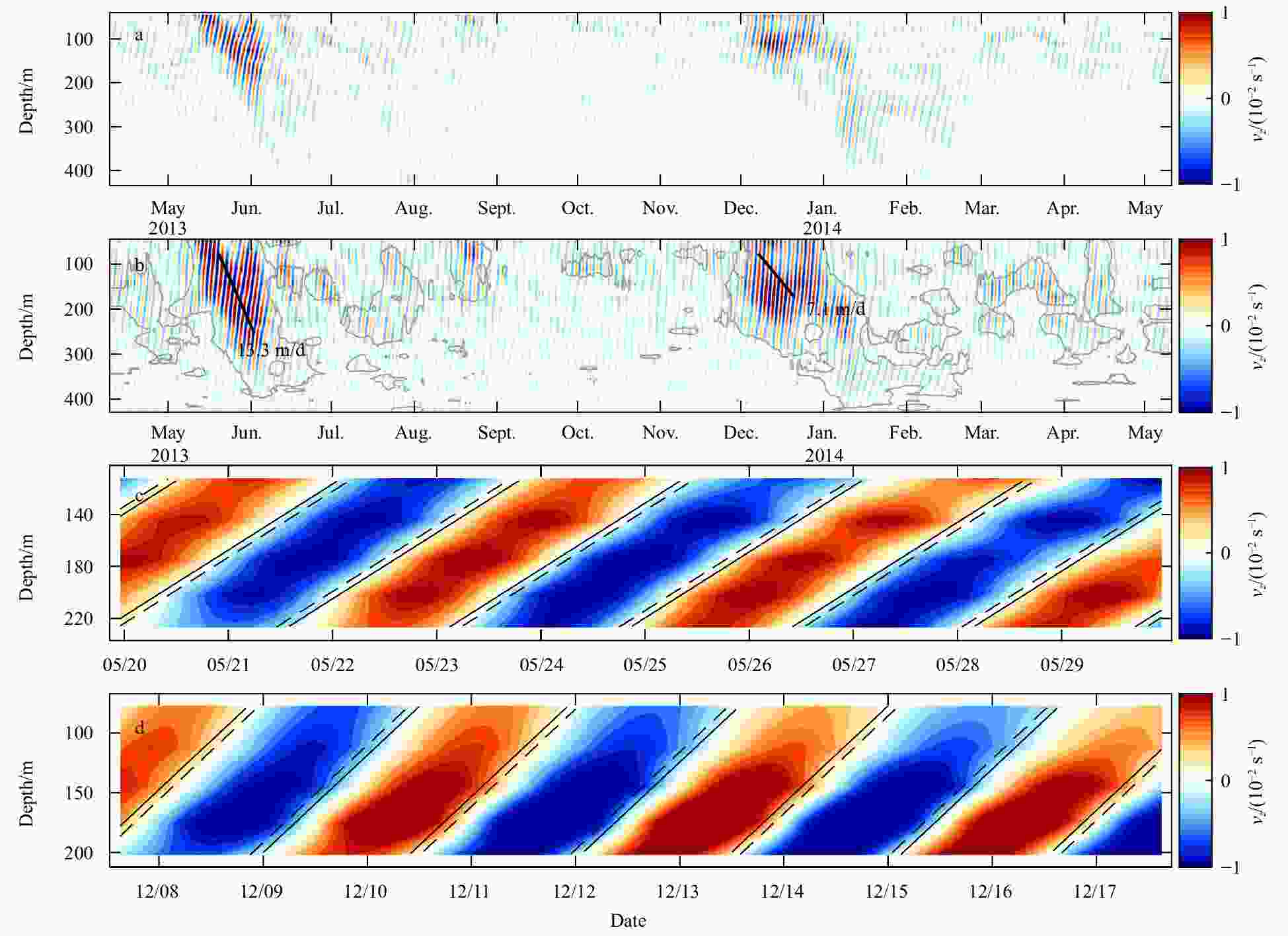
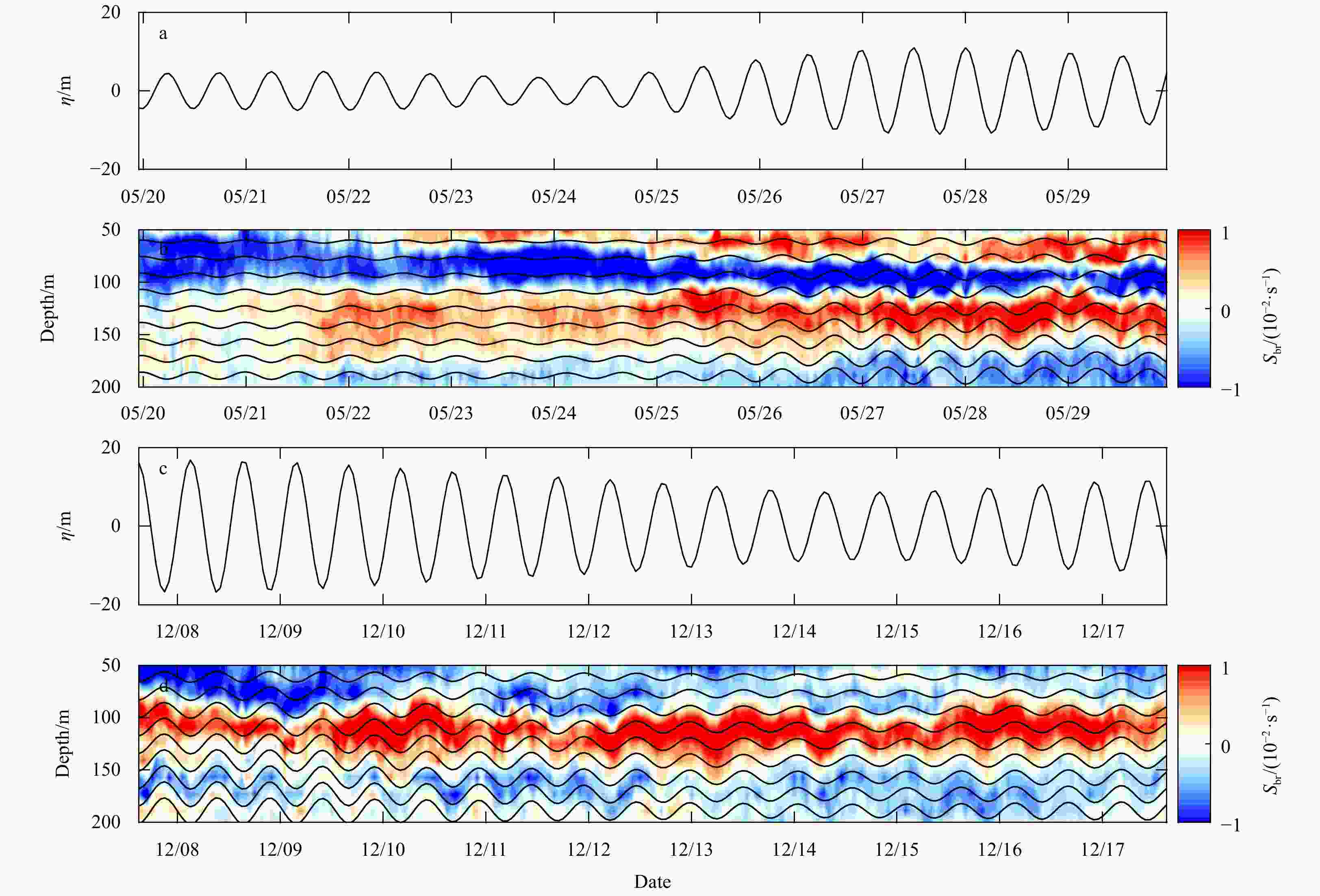
Figure 4. Near-inertial shear and plane wave solutions. a. Bandpass filtered near-inertial meridional shear from April 9, 2013 to May 11, 2014. b. Same as a, but for the bandpass filtered near-inertial meridional shear with WKB scaling. The gray lines give the areas where vector correlation coefficients between the total shear and the near-inertial shear exceeds 0.7. The black lines indicate the rays of NIWs propagating downward, and the group velocity is shown along the side. c. Snapshot of the TC Viyaru case between 112 m and 227 m (stretched depth). The time ticks are in format mm/dd. d. Same as c, but for the TC Madi case between 77 m and 202 m (stretched depth). The solid and dashed lines represent contours of 0.1 and –0.1 of the plane wave solutions, respectively.
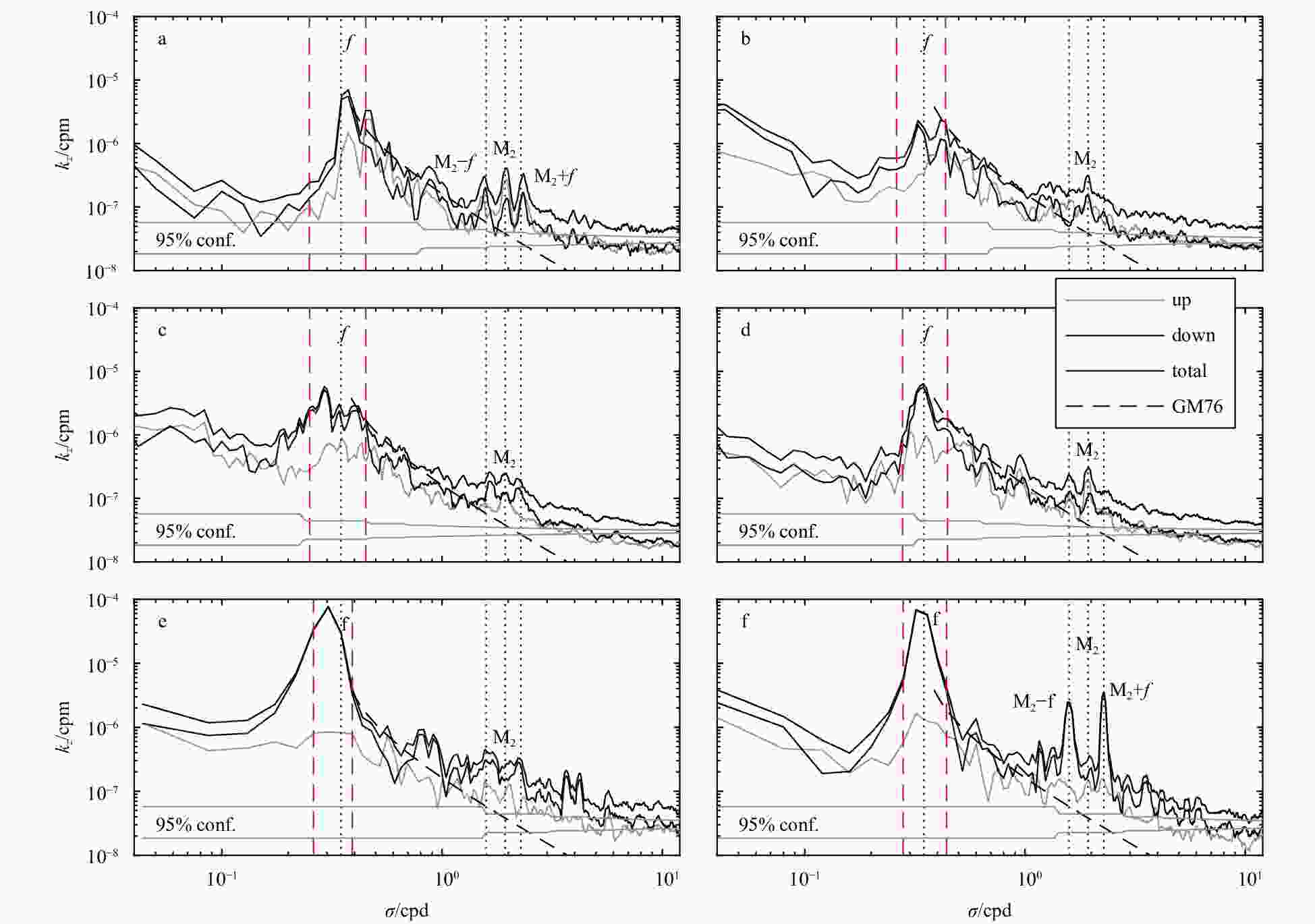
Figure 5. Wavenumber-frequency spectra for different periods. a. Pre-monsoon, b. post-monsoon, c. summer monsoon, d. winter monsoon, e. TC Viyaru, and f. TC Madi. The division of the periods is the same as that presented in Fig. 2. The gray dashed lines represent different frequencies, and the corresponding frequencies are shown. The abscissa is wave frequency, σ, in cycle per day (cpd), and the ordinate is vertical wavenumber, kz, in cycle per meter (cpm).
Figure 6. Rotary frequency spectra for different periods. a. Pre-monsoon, b. post-monsoon, c. summer monsoon, d. winter monsoon, e. TC Viyaru, and f. TC Madi. The red dashed lines indicate the near-inertial frequency bands determined by the ratio of clockwise and counterclockwise components exceeding 3 (see the text). Horizontal gray lines give the confidence intervals of the spectra, with degrees of freedom varying with increasing frequency, σ, in cycle per day (cpd), and the ordinate is vertical wavenumber, kz, in cycle per meter (cpm).
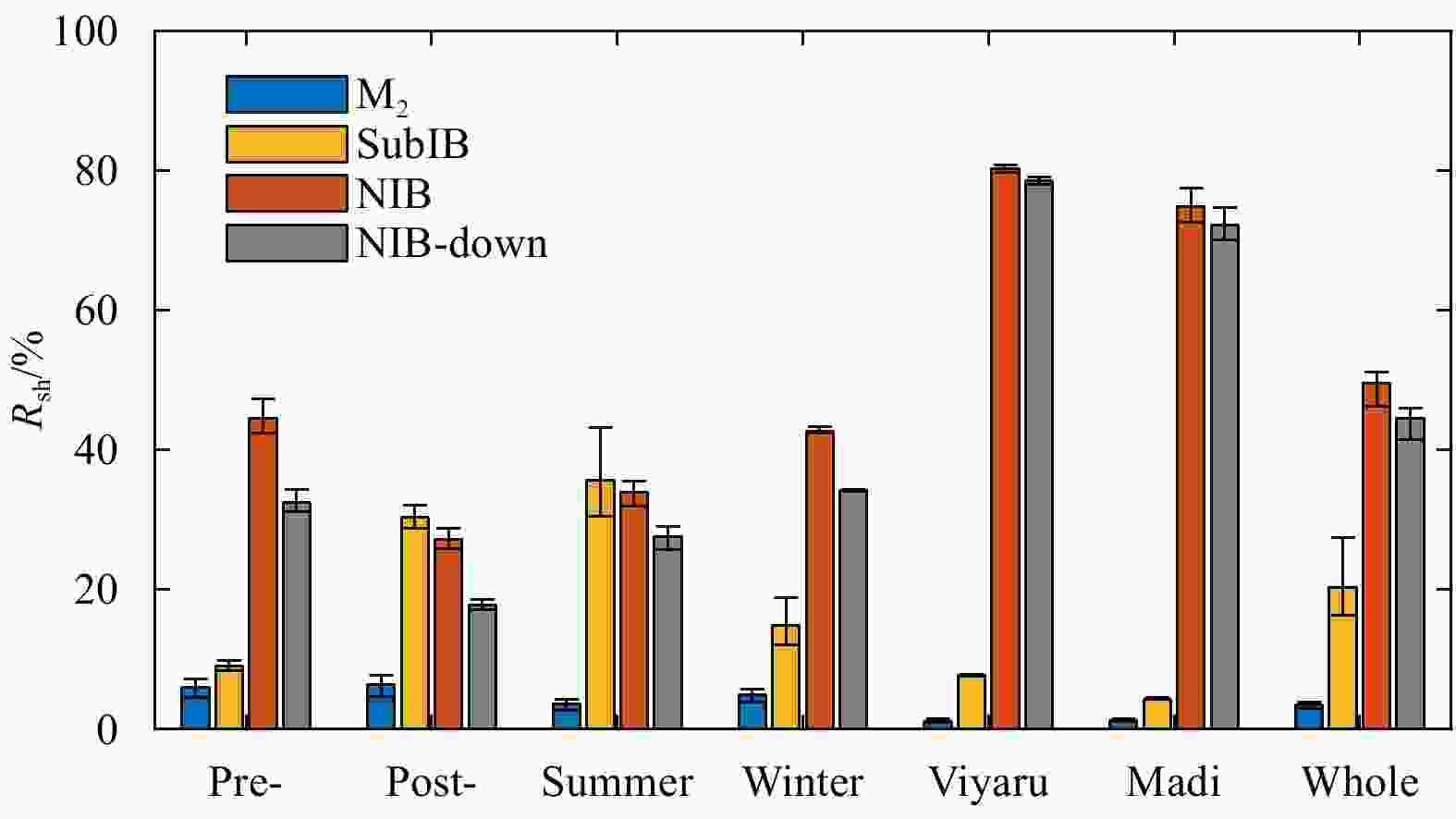
Figure 7. Histogram of the percentage of shear variances in total variances. The error bars were estimated by the corresponding 95% confidence intervals given in Fig. 6.
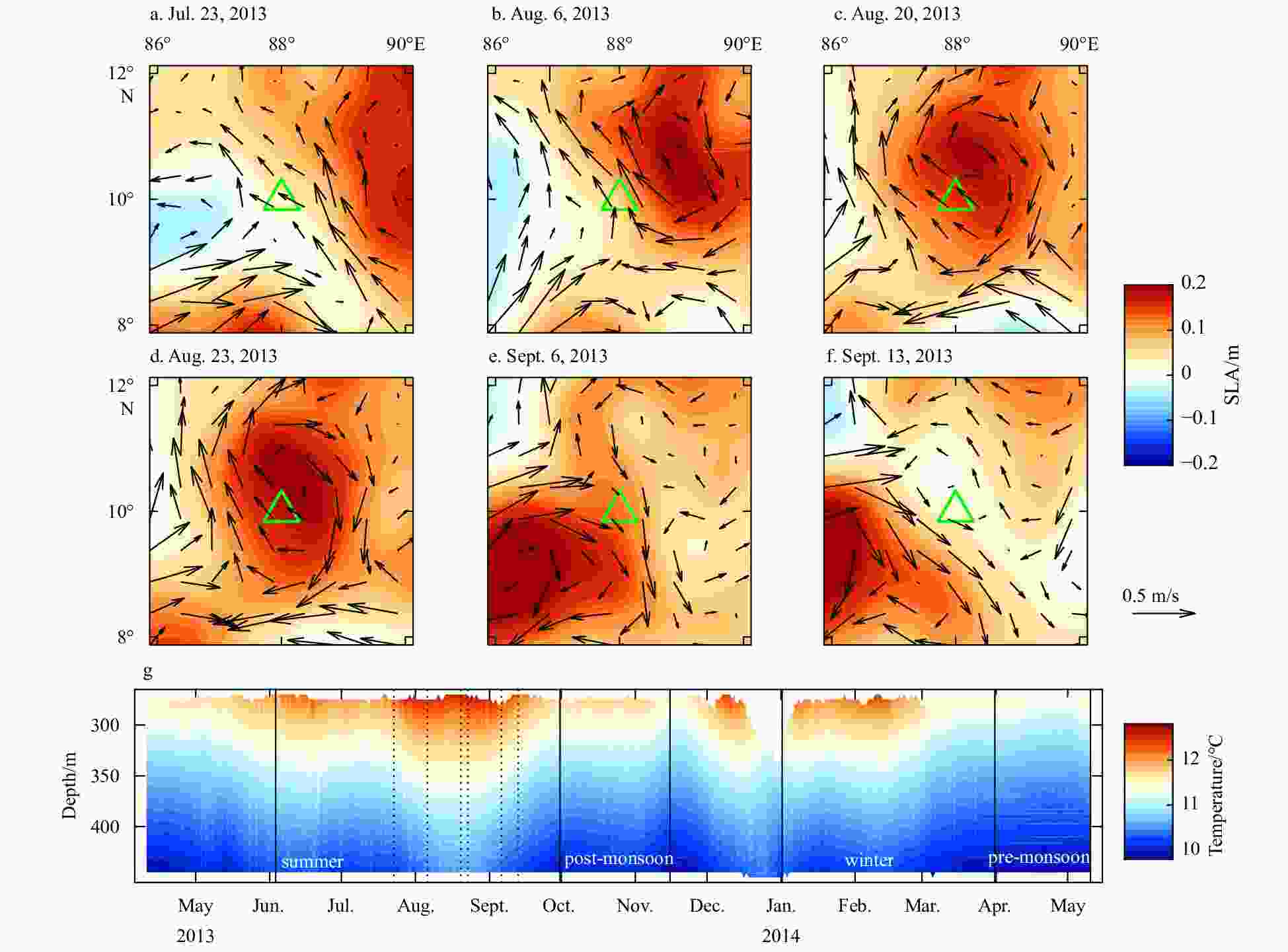
Figure 8. Sea surface anomaly (SLA; a–f) and mooring temperature observations (g) . SLA and surface geostrophic currents correspond to the dates indicated by the dashed lines in g. The green triangle represents the location of the mooring. Contours of temperature data are beneath 280 m in g. The black solid lines in g give four of the six periods indicated by the red dashed lines in Fig. 2.
Figure 9. Backrotated shear and internal tide displacements. M2 tidal components of the isotherm of 11°C for TC Viyaru (May 2013) (a) and TC Madi (December 2013) (b). The corresponding real part of the backrotated shear (Sbr) between 50 m and 200 m with internal tide displacements superimposed (black solid lines) (b, d).
Table 1. Percentage of shear variances in the total variances
Period NIB SubIB M2 Pre-monsoon 44.5 (32.5) 9.0 5.9 (2.6) Post-monsoon 27.2 (17.8) 30.3 6.3 (3.8) Summer monsoon 33.9 (27.6) 35.6 3.6 (2.4) Winter monsoon 42.6 (34.1) 14.8 4.9 (2.7) TC Viyaru 80.2 (78.5) 7.7 1.1 (0.9) TC Madi 74.8 (72.2) 4.3 1.2 (0.90) Whole record 49.5 (44.5) 20.3 3.4 (2.2) Note: The columns give the estimates for near-inertial bands (NIB), subinertial bands (SubIB) and M2 internal tide bands. The values in the parentheses give the percentage of the downward-propagating shear in the total shear. -
[1] Alford M H. 2003. Improved global maps and 54-year history of wind-work on ocean inertial motions. Geophysical Research Letters, 30: 1424 [2] Alford M H, Cronin M F, Klymak J M. 2012. Annual cycle and depth penetration of wind-generated near-inertial internal waves at Ocean Station Papa in the northeast Pacific. Journal of Physical Oceanography, 42: 889–909. doi: 10.1175/JPO-D-11-092.1 [3] Alford M H, Gregg M C. 2001. Near-inertial mixing: Modulation of shear, strain and microstructure at low latitude. Journal of Geophysical Research: Oceans, 106: 16947–16968. doi: 10.1029/2000JC000370 [4] Alford M H, MacKinnon J A, Pinkel R, et al. 2017. Space-time scales of shear in the North Pacific. Journal of Physical Oceanography, 47: 2455–2478. doi: 10.1175/JPO-D-17-0087.1 [5] Alford M H, MacKinnon J A, Simmons H L, et al. 2016. Near-inertial internal gravity waves in the ocean. Annual Review of Marine Science, 8: 95–123. doi: 10.1146/annurev-marine-010814-015746 [6] Breaker L C, Gemmill W H, Dewitt P W, et al. 2003. A curious relationship between the winds and currents at the western entrance of the Santa Barbara Channel. Journal of Geophysical Research, 108: 3132. doi: 10.1029/2002JC001458 [7] Cairns J L, Williams G O. 1976. Internal wave observations from a midwater float. Journal of Geophysical Research, 81: 1943–1950. doi: 10.1029/JC081i012p01943 [8] Cao Anzhou, Guo Zheng, Wang Shuya, et al. 2019. Upper ocean shear in the northern South China Sea. Journal of Oceanography, 75: 525–539. doi: 10.1007/s10872-019-00520-x [9] Cherian D, Shroyer E, Wijesekera H, et al. 2020. The seasonal cycle of upper-ocean mixing at 8°N in the Bay of Bengal. Journal of Physical Oceanography, 50: 323–342. doi: 10.1175/JPO-D-19-0114.1 [10] Chowdary J S, Parekh A, Ojha S, et al. 2016. Impact of upper ocean processes and air-sea fluxes on seasonal SST biases over the tropical Indian Ocean in the NCEP Climate Forecasting System. International Journal of Climatology, 36: 188–207. doi: 10.1002/joc.4336 [11] Garrett C. 2001. What is the “near-inertial” band and why is it different from the rest of the internal wave spectrum?. Journal of Physical Oceanography, 31: 962–971. doi: 10.1175/1520-0485(2001)031<0962:WITNIB>2.0.CO;2 [12] Garrett C, Munk W. 1975. Space-time scales of internal waves: A progress report. Journal of Geophysical Research, 80: 291–297. doi: 10.1029/JC080i003p00291 [13] Gao Jing, Wang Jianing, Wang Fan. 2019. Response of near-Inertial shear to wind stress curl and sea level. Scientific Reports, 9: 1–11 [14] Girishkumar M, Suprit K, Chiranjivi J, et al. 2014. Observed oceanic response to tropical cyclone Jal from a moored buoy in the south-western Bay of Bengal. Ocean Dynamics, 64: 325–335. doi: 10.1007/s10236-014-0689-6 [15] Goswami B, Rao S A, Sengupta D, et al. 2016. Monsoons to mixing in the Bay of Bengal: Multiscale air-sea interactions and monsoon predictability. Oceanography, 29: 18–27 [16] Jochum M, Briegleb B P, Danabasoglu G, et al. 2013. The impact of oceanic near-inertial waves on climate. Journal of Climate, 26: 2833–2844. doi: 10.1175/JCLI-D-12-00181.1 [17] Johnston T S, Chaudhuri D, Mathur M, et al. 2016. Decay mechanisms of near-inertial mixed layer oscillations in the Bay of Bengal. Oceanography, 29: 180–191. doi: 10.5670/oceanog.2016.50 [18] Köhler J, Völker G S, Walter M. 2018. Response of the internal wave field to remote wind forcing by tropical cyclones. Journal of Physical Oceanography, 48: 317–328. doi: 10.1175/JPO-D-17-0112.1 [19] Leaman K D, Sanford T B. 1975. Vertical energy propagation of inertial waves: A vector spectral analysis of velocity profiles. Journal of Geophysical Research, 80: 1975–1978. doi: 10.1029/JC080i015p01975 [20] Majumder S, Tandon A, Rudnick D L, et al. 2015. Near inertial kinetic energy budget of the mixed layer and shear evolution in the transition layer in the Arabian Sea during the monsoons. Journal of Geophysical Research: Oceans, 120: 6492–6507. doi: 10.1002/2014JC010198 [21] Pinkel R. 2008. Advection, phase distortion, and the frequency spectrum of finescale fields in the sea. Journal of Physical Oceanography, 38: 291–313. doi: 10.1175/2007JPO3559.1 [22] Rimac A, von Storch J S, Eden C, et al. 2013. The influence of high-resolution wind stress field on the power input to near-inertial motions in the ocean. Geophysical Research Letters, 40: 4882–4886. doi: 10.1002/grl.50929 [23] Saha S, Coauthors. 2014. The NCEP Climate Forecast System Version 2. Journal of Climate, 27: 2185–2208. doi: 10.1175/JCLI-D-12-00823.1 [24] Schott F A, Xie S P, McCreary J P. 2009. Indian Ocean circulation and climate variability. Reviews of Geophysics, 47: RG1002 [25] Varkey M J, Murty V S, Suryanarayana A. 1996. Physical oceanography of the Bay of Bengal and Andaman Sea. Oceanography and Marine Biology, 34: 1–70 -




 下载:
下载: