The construction of high precision geostrophic currents based on new gravity models of GOCE and satellite altimetry data
-
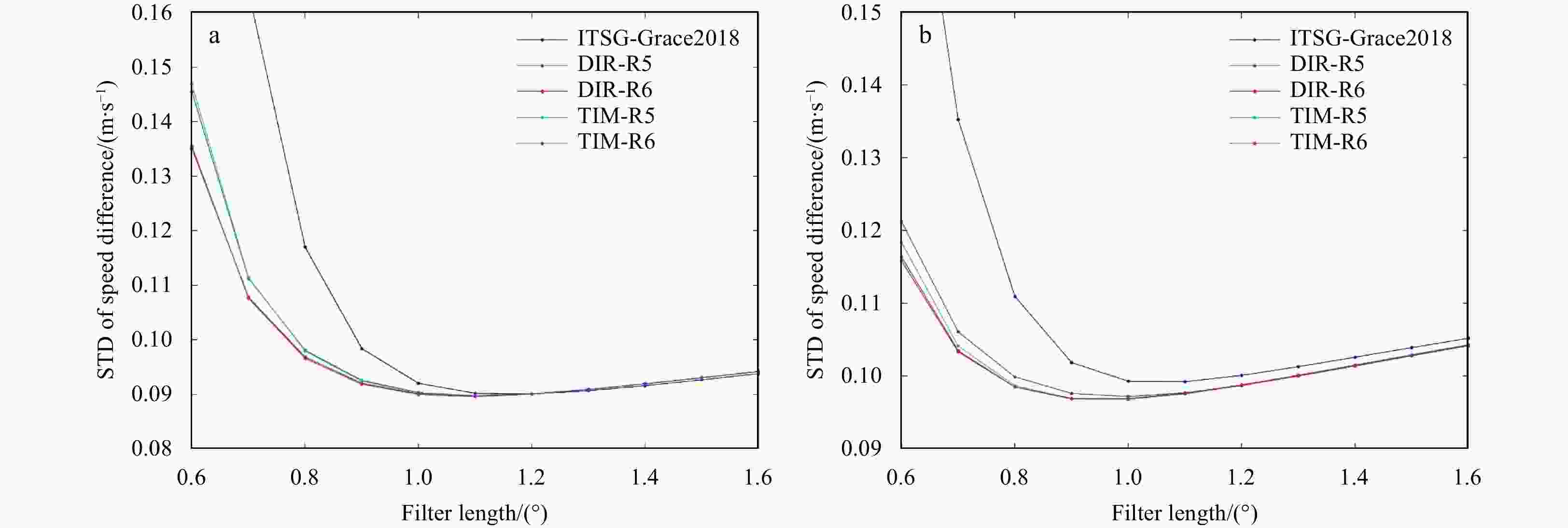
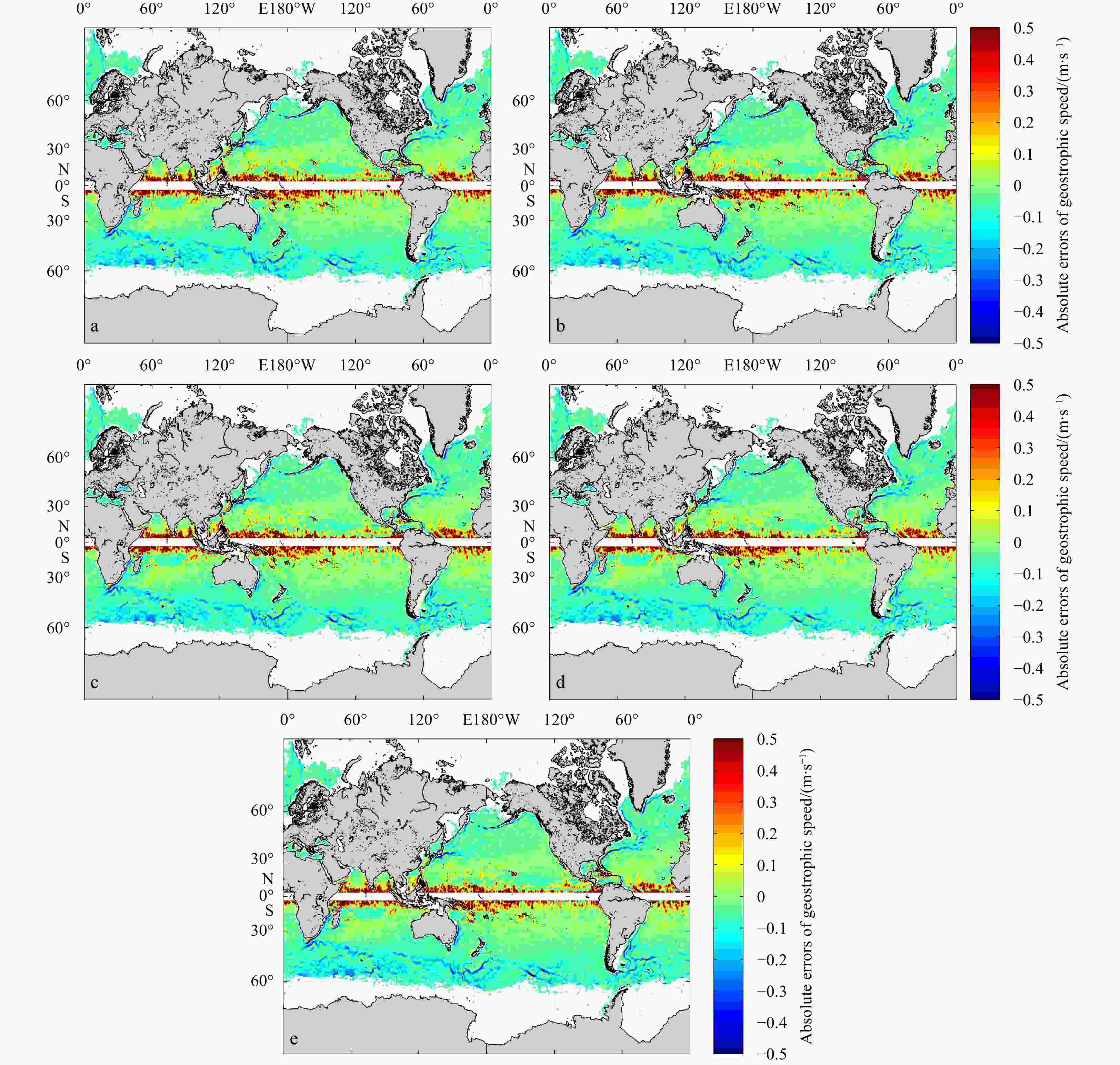
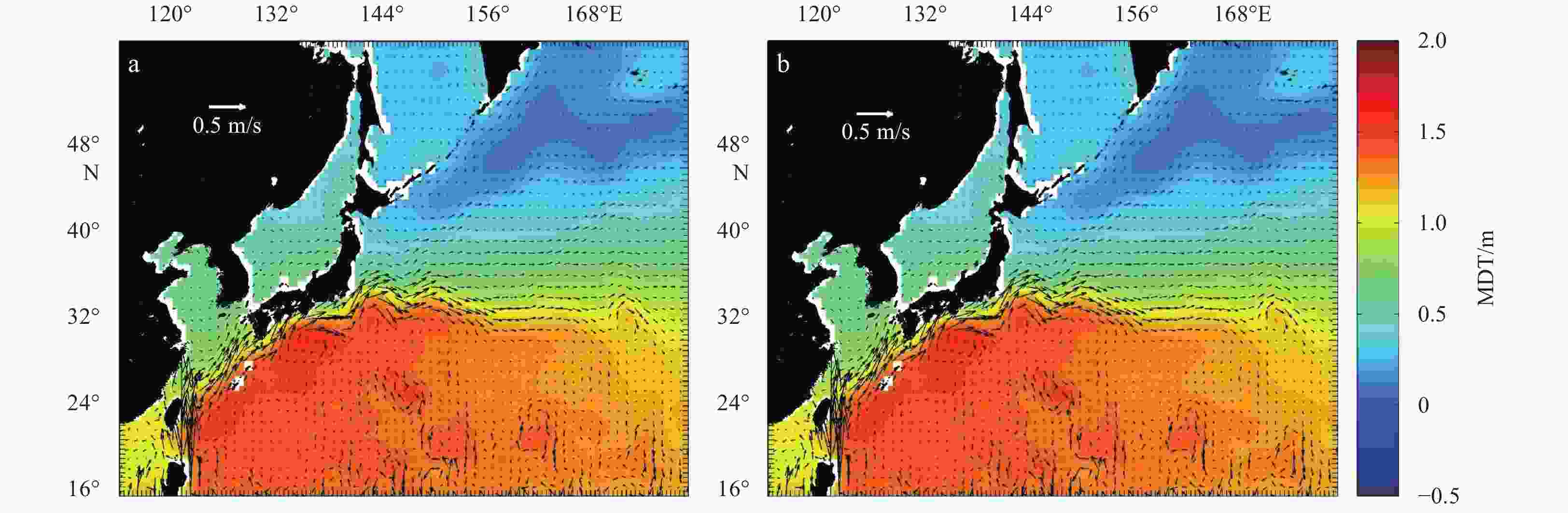
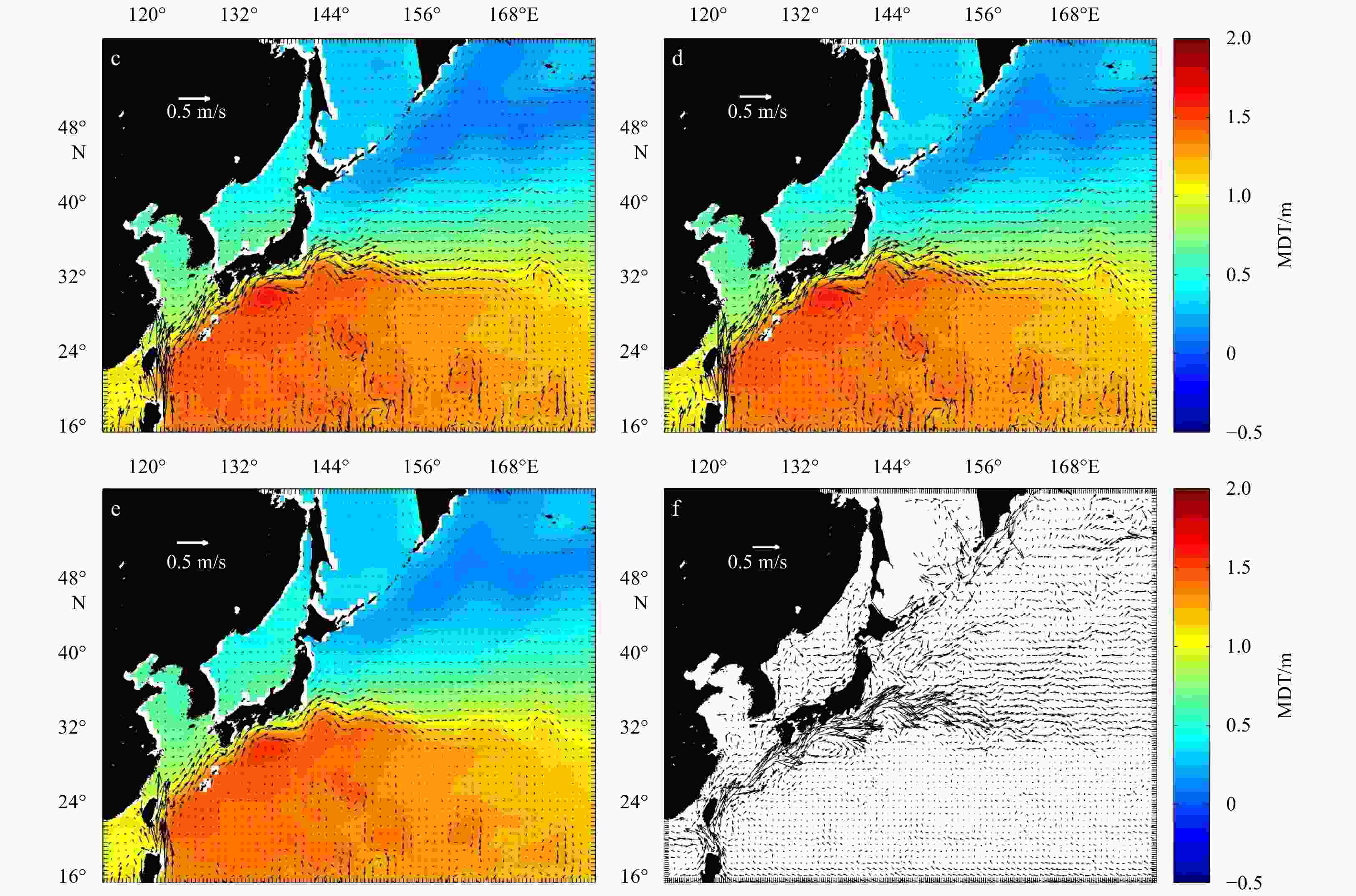
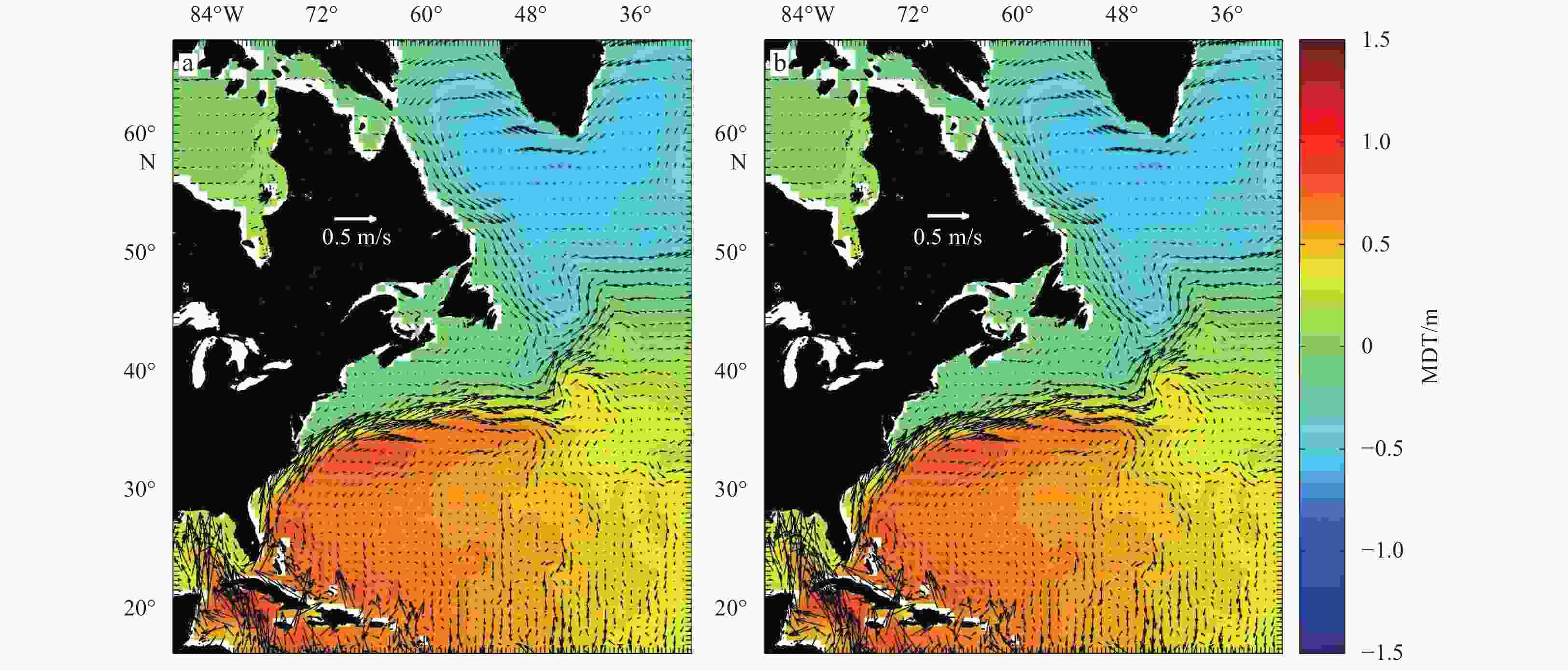
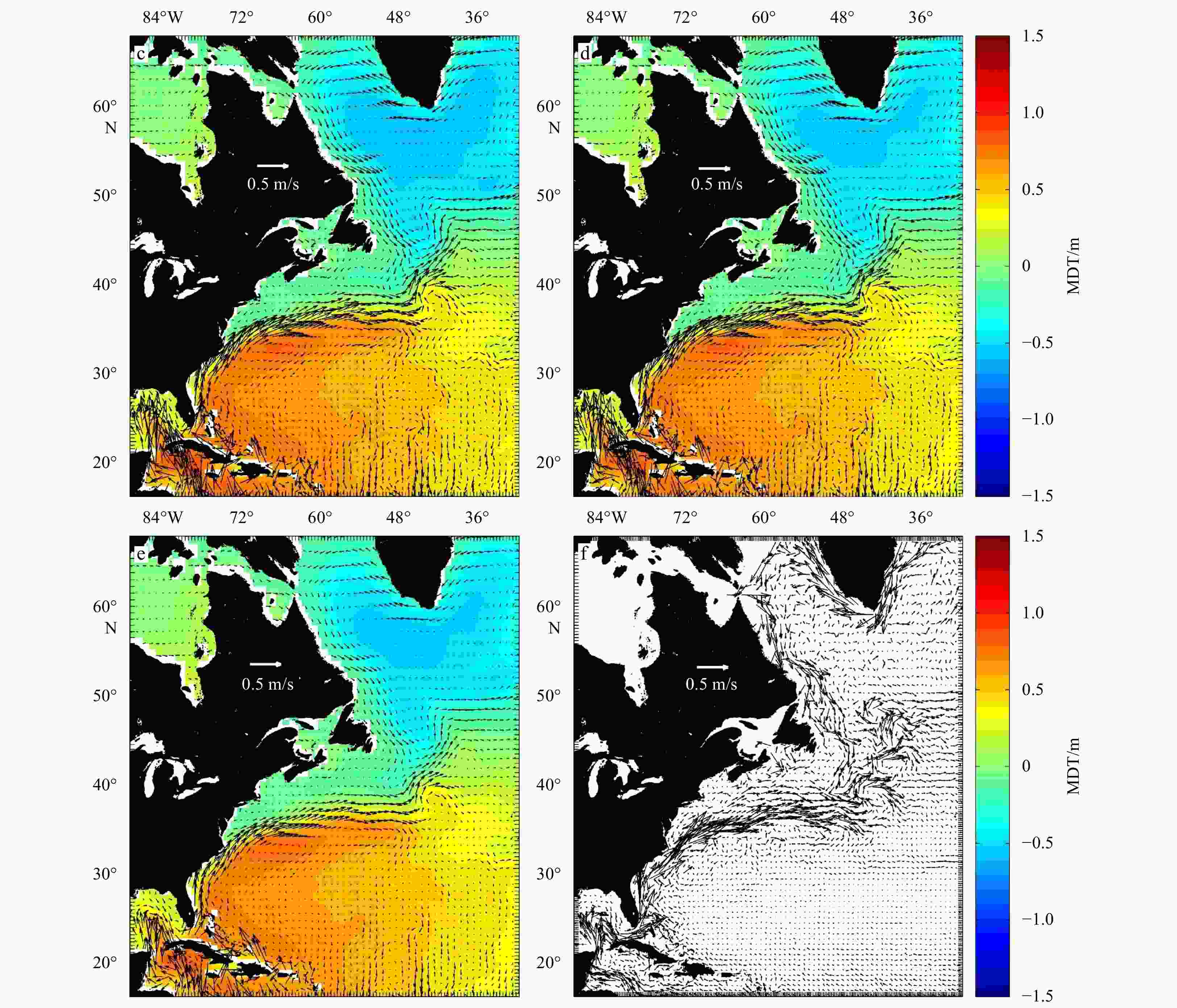
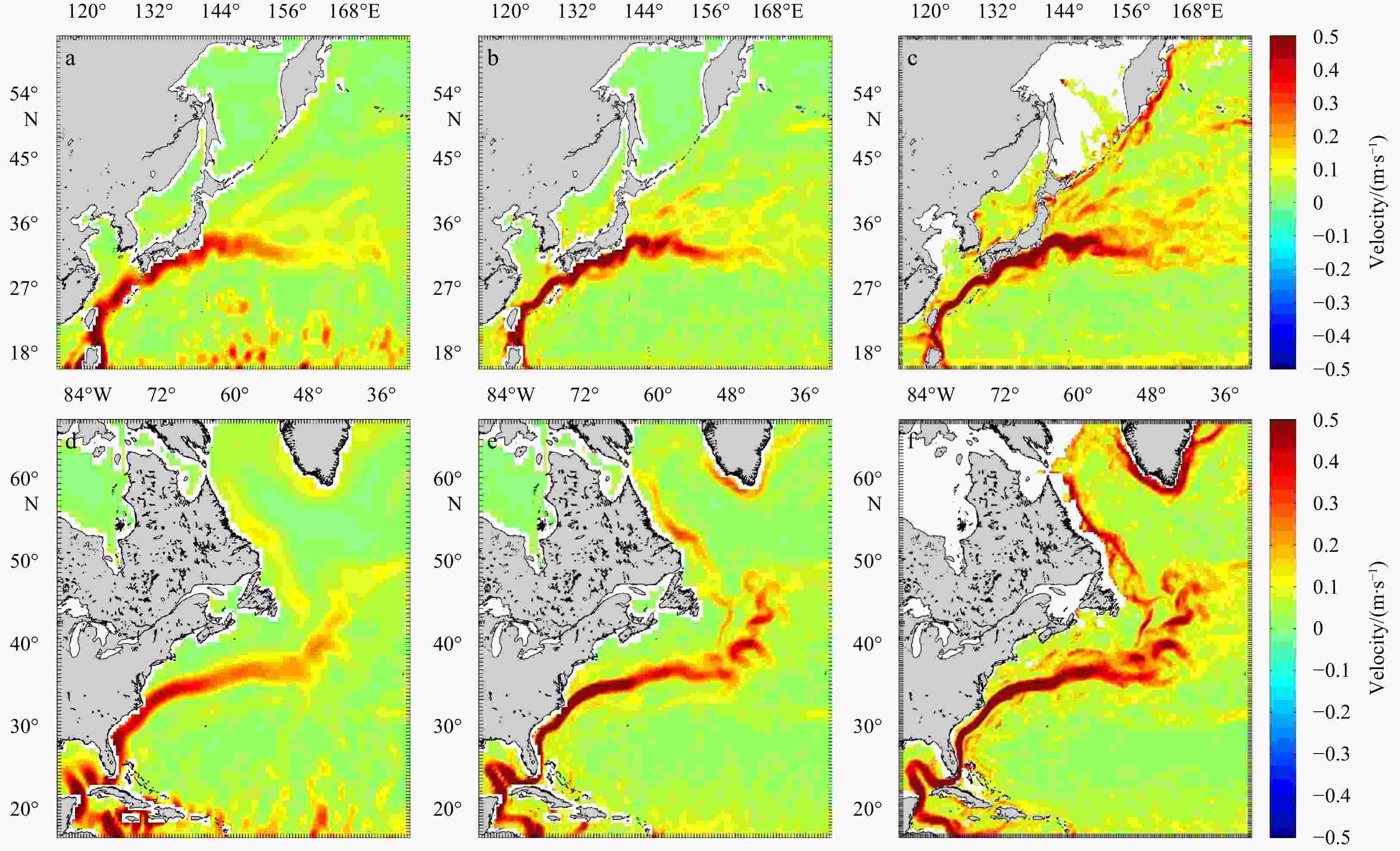
Abstract: The new gravity field models of gravity field and steady-state ocean circulation explorer (GOCE), TIM_R6 and DIR_R6, were released by the European Space Agency (ESA) in June 2019. The sixth generation of gravity models have the highest possible signal and lowest error levels compared with other GOCE-only gravity models, and the accuracy is significantly improved. This is an opportunity to build high precision geostrophic currents. The mean dynamic topography and geostrophic currents have been calculated by the 5th (TIM_R5 and DIR_R5), 6th (TIM_R6 and DIR_R6) release of GOCE gravity field models and ITSG-Grace2018 of GRACE gravity field model in this study. By comparison with the drifter results, the optimal filtering lengths of them have been obtained (for DIR_R5, DIR_R6, TIM_R5 and TIM_R6 models are 1° and for ITSG-Grace2018 model is 1.1°). The filtered results show that the geostrophic currents obtained by the GOCE gravity field models can better reflect detailed characteristics of ocean currents. The total geostrophic speed based on the TIM_R6 model is similar to the result of the DIR_R6 model with standard deviation (STD) of 0.320 m/s and 0.321 m/s, respectively. The STD of the total velocities are 0.333 m/s and 0.325 m/s for DIR_R5 and TIM_R5. When compared with ITSG-Grace2018 results, the STD (0.344 m/s) of total geostrophic speeds is larger than GOCE results, and the accuracy of geostrophic currents obtained by ITSG-Grace2018 is lower. And the absolute errors are mainly distributed in the areas with faster speeds, such as the Antarctic circumpolar circulation, equatorial region, Kuroshio and Gulf Stream areas. After the remove-restore technique was applied to TIM_R6 MDT, the STD of total geostrophic speeds dropped to 0.162 m/s.
-
Key words:
- GOCE /
- gravity field model /
- mean dynamic topography /
- geostrophic current
-
Figure 1. Comparison of geoid heights from different GOCE gravity field models. a. DIR_R5-DIR_R6 model, b. DIR_R5-TIM_R5 model, c. DIR_R5-TIM_R6 model, d. DIR_R6-TIM_R5 model, e. DIR_R6-TIM_R6 model, and f. TIM_R5-TIM_R6 model.
Figure 2. Comparison of geoid heights from GRACE and GOCE gravity field models. a. ITSG-Grace2018-DIR_R5 model, b. ITSG-Grace2018-DIR_R6 model, c. ITSG-Grace2018-TIM_R5 model, and d. ITSG-Grace2018-TIM_R6 model.
Figure 4. Standard errors of drifters’ eastward velocities (a) and northward velocities (b).
Figure 5. Standard errors of the total geostrophic speed differences between gravity models and drifter in Kuroshio area (a) and Gulf Stream area (b).
Figure 6. The absolute errors of total geostrophic speeds calculated by different gravity field models. a. DIR_R5-drifter model, b. DIR_R6-drifter model, c. TIM_R5-drifter model, d. TIM_R6-drifter model, and e. ITSG-Grace2018-drifter model.
Figure 7. Mean dynamic topography (shadding) and corresponding geostrophic currents (black arrows) in the Kuroshio area. a. DIR_R5 model, b. DIR_R6 model, c. TIM_R5 model, d. TIM_R6 model, e. ITSG-Grace2018, and f. drifter.
Figure 8. Mean dynamic topography and corresponding geostrophic currents (velocities are displayed as black arrows) in the Gulf Stream area. a. DIR_R5 model, b. DIR_R6 model, c. TIM_R5 model, d. TIM_R6 model, e. ITSG- Grace2018 model, and f. drifter.
Figure 9. Comparison of total geostrophic speeds before and after Remove-restore technique in the Kuroshio current area (a. before remove-restore, b. after remove-restore, and c. drifter) and Gulf Stream area (d. before remove-restore, e. after remove-restore, and f. drifter).
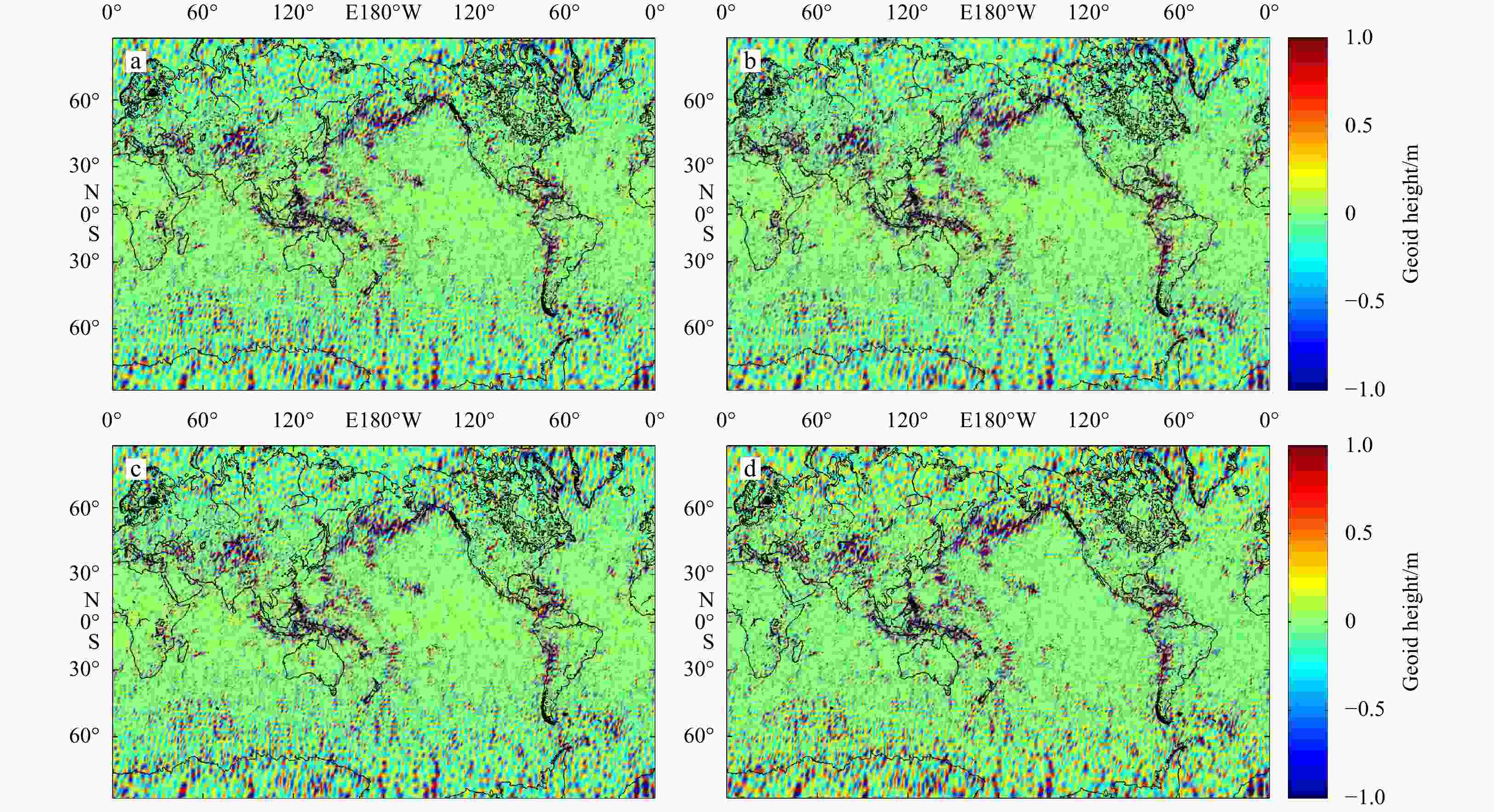
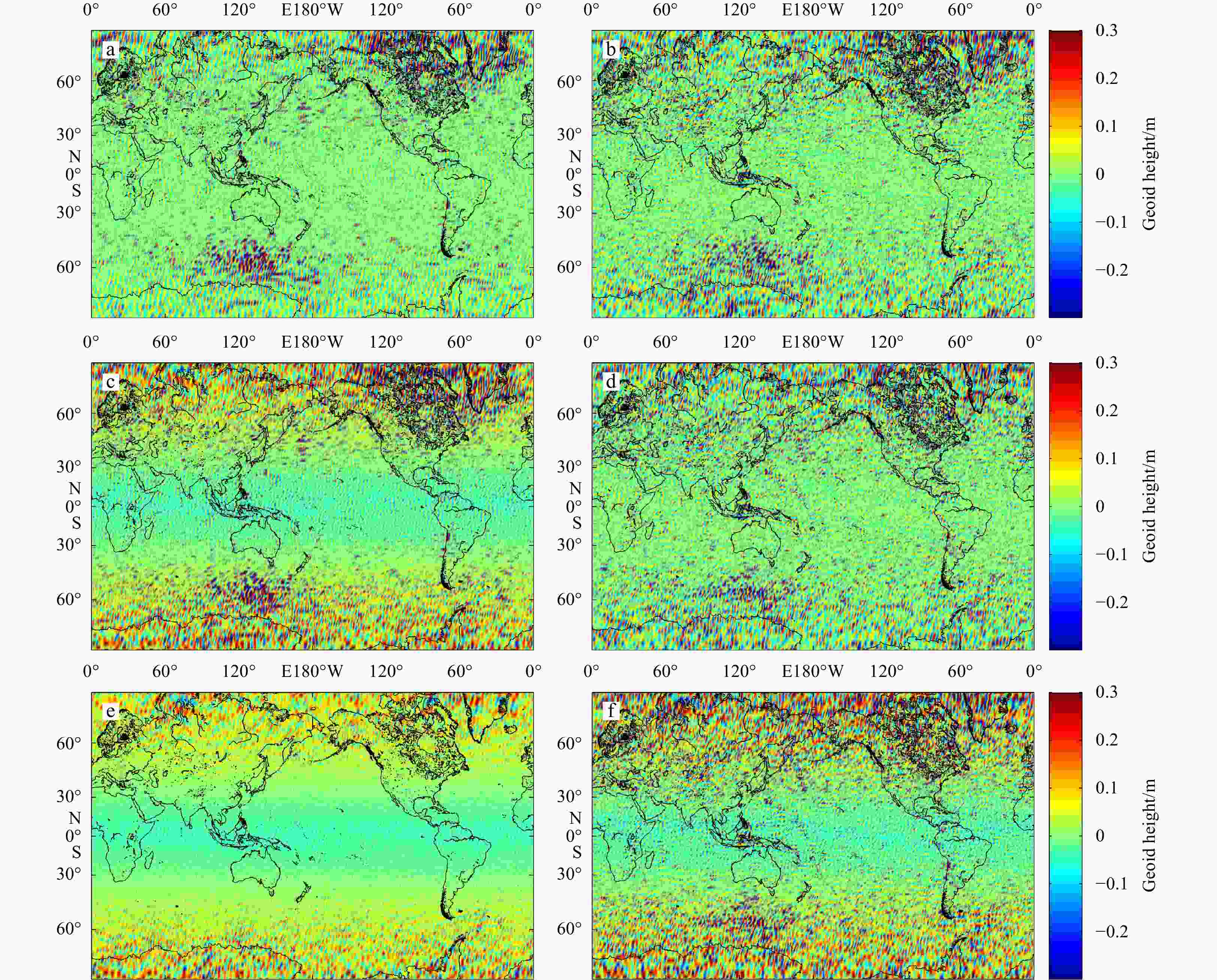
Table 1. Statistics of the different geoid products
Gravity model Mean geoid height/m RMS/m Minmum geoid height/m Maxmum geoid height/m DIR_R5-DIR_R6 0.001 0.147 –1.878 1.853 DIR_R5-TIM_R5 0.006 0.246 –2.624 3.286 DIR_R5-TIM_R6 0.006 0.251 –2.812 2.580 DIR_R6-TIM_R5 0.005 0.209 –2.360 2.167 DIR_R6-TIM_R6 0.005 0.207 –2.785 2.461 TIM_R5-TIM_R6 0.000 0.284 –2.463 3.510 ITSG-Grace2018-DIR_R5 –0.014 0.349 –3.423 2.337 ITSG-Grace2018-DIR_R6 –0.013 0.323 –3.506 2.419 ITSG-Grace2018-TIM_R5 –0.008 0.373 –3.331 2.342 ITSG-Grace2018-TIM_R6 –0.007 0.383 –3.655 3.322 
下载: 导出CSV
Table 2. STD between the geostrophic currents based on GRACE/GOCE models and drifter results
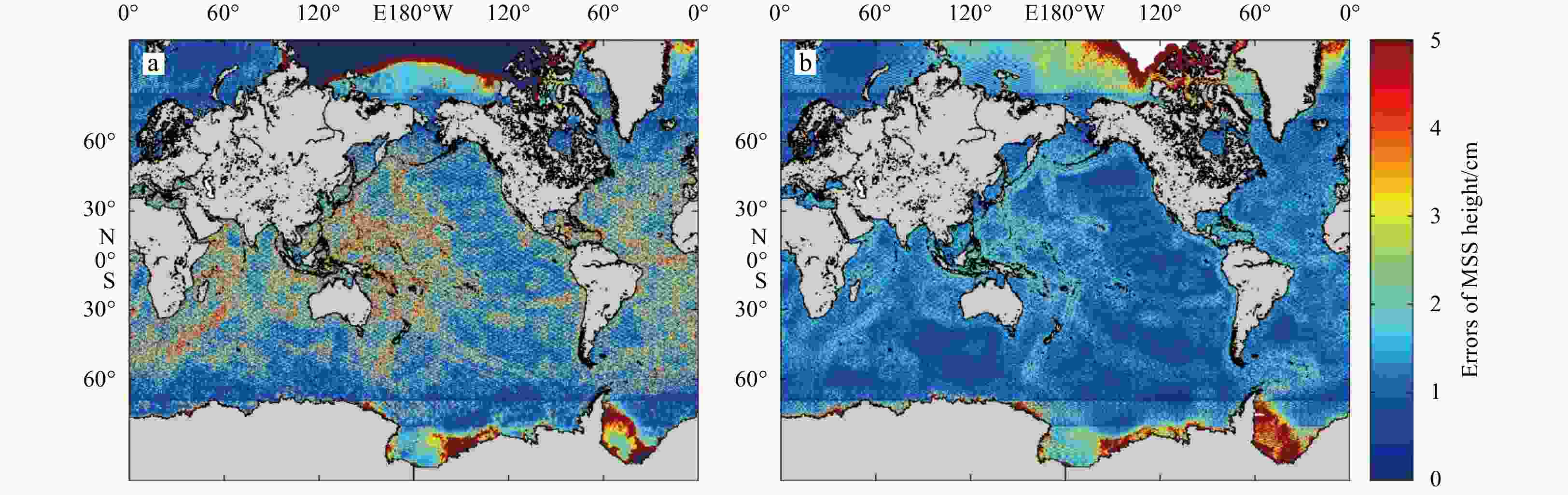
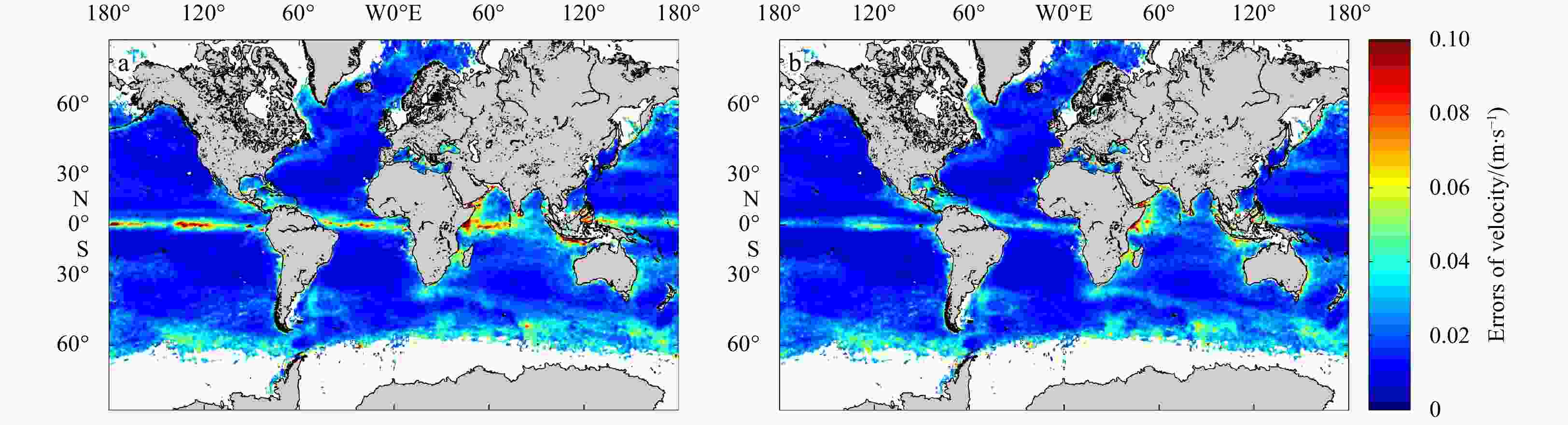
Gravity field model Unfiltered velocity Filtered velocity STD (u)/(m·s–1) STD (v)/(m·s–1) STD (V)/(m·s–1) STD (u)/(m·s–1) STD (v)/(m·s–1) STD (V)/(m·s–1) DIR_R5 0.771 7.830 12.375 0.091 0.367 0.333 DIR_R6 0.765 7.567 12.118 0.091 0.355 0.321 TIM_R5 0.786 7.706 12.251 0.091 0.359 0.325 TIM_R6 0.767 7.404 11.907 0.091 0.353 0.320 ITSG-Grace2018 1.293 11.702 16.186 0.097 0.377 0.344
下载: 导出CSV
Table 3. STD of geostrophic currents between the different MDT and drifter results
MDT models STD of geostrophic current/(m·s–1) STD (u) STD (v) STD (V) TIM_R6 before remove-restore 0.091 0.353 0.320 TIM_R6 after Remove-restore 0.077 0.209 0.162 MDT_CNES-CLS13 0.080 0.233 0.186
下载: 导出CSV
-
[1] Albertella A, Savcenko R, Janjić T, et al. 2012. High resolution dynamic ocean topography in the southern ocean from GOCE. Geophysical Journal Interna-tional, 190(2): 922–930. doi: 10.1111/j.1365-246X.2012.05531.x [2] Andersen O, Knudsen P, Stenseng L. 2015. The DTU13 MSS (mean sea surface) and MDT (mean dynamic topography) from 20 years of Satellite Altimetry. In: Jin S, Barzaghi R, eds. IGFS 2014. International Association of Geodesy Symposia, Vol 144. Shanghai, China: Springer, Cham: 111–121 [3] Bingham R J, Haines K, Hughes C W. 2008. Calculating the ocean’s mean dynamic topography from a mean sea surface and a geoid. Journal of Atmospheric and Oceanic Technology, 25(10): 1808–1822. doi: 10.1175/2008JTECHO568.1 [4] Bingham R J, Haines K, Lea D. 2015. A comparison of GOCE and drifter-based estimates of the North Atlantic steady-state surface circulation. International Journal of Applied Earth Observation and Geoinformation, 35: 140–150. doi: 10.1016/j.jag.2014.03.012 [5] Bingham R J, Knudsen P, Andersen O, et al. 2011. An initial estimate of the North Atlantic steadystate geostrophic circulation from GOCE. Geophysical Research Letters, 38(1): L01606. doi: 10.1029/2010GL045633 [6] Brockmann J M, Schubert T, Mayer-Gürr T, et al. 2019. The Earth’s gravity field as seen by the GOCE satellite—An improved sixth release derived with the time-wise approach (GO_CONS _GCF_2_TIM_R6). GFZ Data Services [7] Brockmann J M, Zehentner N, Höck E, et al. 2014. EGM_TIM_RL05: An independent geoid with centimeter accuracy purely based on the GOCE mission. Geophysical Research Letters, 41(22): 8089–8099. doi: 10.1002/2014GL061904 [8] Bruinsma S L, Förste C, Abrikosov O, et al. 2013. The new ESA satellite-only gravity field model via the direct approach. Geophysical Research Letters, 40(14): 3607–3612. doi: 10.1002/grl.50716 [9] Bruinsma S L, Förste C, Abrikosov O, et al. 2014. ESA’s satellite-only gravity field model via the direct approach based on all GOCE data. Geophysical Research Letters, 41(21): 7508–7514. doi: 10.1002/2014GL062045 [10] Feng Guiping, Jin Shuanggen, Reales J M S. 2013. Antarctic circumpolar current from satellite gravimetric models ITG-GRACE2010, GOCE-TIM3 and satellite altimetry. Journal of Geodynamics, 72: 72–80. doi: 10.1016/j.jog.2013.08.005 [11] Förste C, Abrykosov O, Bruinsma S, et al. 2019. ESA’s Release 6 GOCE gravity field model by means of the direct approach based on improved filtering of the reprocessed gradients of the entire mission (GO_CONS_GCF_2_DIR_R6). GFZ Data Services, https://doi.org/10.5880/ICGEM.2019.004 [12] Förste C, Schmidt R, Stubenvoll R, et al. 2008. The GeoForschungs Zentrum Potsdam/Groupe de Recherche de Gèodésie Spatiale satellite-only and combined gravity field models: EIGEN-GL04S1 and EIGEN-GL04C. Journal of Geodesy, 82(6): 331–346. doi: 10.1007/s00190-007-0183-8 [13] Haines K, Johannessen J A, Knudsen P, et al. 2011. An ocean modelling and assimilation guide to using GOCE geoid products. Ocean Science, 7(1): 151–164. doi: 10.5194/os-7-151-2011 [14] Jin Shuanggen, Feng Guiping, Andersen O. 2014. Errors of mean dynamic topography and geostrophic current estimates in China’s marginal seas from GOCE and satellite altimetry. Journal of Atmos-pheric and Oceanic Technology, 31(11): 2544–2555. doi: 10.1175/JTECH-D-13-00243.1 [15] Knudsen P, Andersen O, Maximenko N. 2019. A new ocean mean dynamic topography model, derived from a combination of gravity, altimetry and drifter velocity data. Advances in Space Research: [16] Knudsen P, Bingham R, Andersen O B, et al. 2011a. Enhanced mean dynamic topography and ocean circulation estimation using GOCE preliminary models. In: Proceedings of the 4th International GOCE User Workshop. Munich, Germany: European Space Agency [17] Knudsen P, Bingham R, Andersen O, et al. 2011b. A global mean dynamic topography and ocean circulation estimation using a preliminary GOCE gravity model. Journal of Geodesy, 85(11): 861–879. doi: 10.1007/s00190-011-0485-8 [18] Kvas A, Mayer-Gürr T, Krauss S, et al. 2019. The satellite-only gravity field model GOCO06s. GFZ Data Services, https://doi. org/10.5880/ICGEM.2019.002 [19] Laurindo L C, Mariano A J, Lumpkin R. 2017. An improved near-surface velocity climatology for the global ocean from drifter observations. Deep Sea Research Part I: Oceanographic Research Papers, 124: 73–92. doi: 10.1016/j.dsr.2017.04.009 [20] Lumpkin R, Grodsky S A, Centurioni L, et al. 2013. Removing spurious low-frequency variability in drifter velocities. Journal of Atmospheric and Oceanic Technology, 30(2): 353–360. doi: 10.1175/JTECH-D-12-00139.1 [21] Lumpkin R, Johnson G C. 2013. Global ocean surface velocities from drifters: Mean, variance, El Niño-Southern Oscillation response, and seasonal cycle. Journal of Geophysical Research: Oceans, 118(6): 2992–3006. doi: 10.1002/jgrc.20210 [22] Mayer-Gürr T, Behzadpur S, Ellmer M, et al. 2018. ITSG-Grace2018-monthly, daily and static gravity field solutions from GRACE. GFZ Data Services [23] Pail R, Bruinsma S, Migliaccio F, et al. 2011. First GOCE gravity field models derived by three different approaches. Journal of Geodesy, 85(11): 819–843. doi: 10.1007/s00190-011-0467-x [24] Pail R, Goiginger H, Schuh W D, et al. 2010. Combined satellite gravity field model GOCO01S derived from GOCE and GRACE. Geophysical Research Letters, 37(20): L20314. doi: 10.1029/2010GL044906 [25] Pavlis N K, Holmes S A, Kenyon S C, et al. 2008. An earth gravitational model to degree 2160: EGM2008. In: Proceedings of the 2008 General Assembly of the European Geosciences Union. Vienna, Austria: European Geosciences Union [26] Rio M H, Mulet S, Picot N. 2014. Beyond GOCE for the ocean circulation estimate: Synergetic use of altimetry, gravimetry, and in situ data provides new insight into geostrophic and Ekman currents. Geophysical Research Letters, 41(24): 8918–8925. doi: 10.1002/2014GL061773 [27] Schaeffer P, Faugére Y, Legeais J F, et al. 2012. The CNES_CLS11 global mean sea surface computed from 16 years of satellite altimeter data. Marine Geodesy, 35(Sup1): 3–19. doi: 10.1080/01490419.2012.718231 [28] Siegismund F. 2013. Assessment of optimally filtered recent geodetic mean dynamic topographies. Journal of Geophysical Research: Oceans, 118(1): 108–117. doi: 10.1029/2012JC008149 [29] Sjöberg L E. 2005. A discussion on the approximations made in the practical implementation of the remove-compute-restore technique in regional geoid modelling. Journal of Geodesy, 78(11–12): 645–653 [30] Tsoulis D, Patlakis K. 2013. A spectral assessment review of current satellite-only and combined Earth gravity models. Reviews of Geophysics, 51(2): 186–243. doi: 10.1002/rog.20012 -
点击查看大图
计量
- 文章访问数: 561
- HTML全文浏览量: 161
- PDF下载量: 31
- 被引次数: 0
