Coastal phytoplankton blooms and multivariate analysis with meteorological factors and climate oscillation signals in western North Pacific

1. Introduction

Coastal ecosystems have attracted significant attention due to their vulnerability to climate variability and their critical economic and social importance to human communities (Dai et al., 2023; Waltham et al., 2020). These dynamic ecosystems, situated at the interface of land and sea, exhibit heightened sensitivity to climate oscillations, which is primarily attributed to the intricate interplay between atmospheric forces, nutrient inputs, and the transport of propagules within marine environments (Carstensen et al., 2015). Phytoplankton, a pivotal link between higher trophic level organisms and the climate, plays a crucial role in carbon fixation, forming the foundation of the food chain and supporting global fisheries and ecosystems (Defriez et al., 2016). The significance of phytoplankton extends to its role in facilitating energy flow, material circulation, and information transfer within marine ecosystems (Behrenfeld et al., 2001; Sun et al., 2022). Understanding the factors driving phytoplankton blooms is crucial for studying the interplay between climate oscillations and coastal ecosystems.

Phytoplankton growth is influenced by several meteorological factors such as increasing irradiance, temperature, and precipitation (Colijn and Cadée, 2003; Glé et al., 2007). Sea surface temperature (SST) is a major driver, determining bloom timing and intensity in many regions (Xiao et al., 2019). Global warming-induced increases in water temperature alter the timing and amplitude of blooms, impacting the survival and development of commercially important species (Koeller et al., 2009; Platt et al., 2003). While this effect is well-documented in the open ocean, coastal zones present added complexity due to land-sea interactions (Liu et al., 2024). Warmer conditions also shift plankton community composition and trophic interactions, further influencing higher trophic levels (Sommer and Lengfellner, 2008; Vidussi et al., 2011).

Despite its importance, the impact of global climate change on phytoplankton blooms in coastal areas remains underexplored (Menge et al., 2009). Climate change acts as a potential catalyst for bloom expansion, affecting physical, chemical, and biological processes in aquatic environments (Paerl et al., 2011; Paerl and Paul, 2012). Coastal waters, with their higher reactivity and lower inertia compared to open-ocean systems, are particularly sensitive to environmental fluctuations (Rabalais et al., 2009).

Climate oscillation signals quantify changes in climate due to large-scale circulation patterns. Indices such as the Southern Oscillation Index (SOI), Niño3.4, and the Pacific Decadal Oscillation (PDO), serve as effective predictors of phytoplankton blooms, given their influence on meteorological factors (Jochum et al., 2010). Several studies have explored the impacts of climate oscillations on phytoplankton in the western North Pacific, though most have focused on the influence of the El Niño-Southern Oscillation (ENSO) at the annual time scale (Doan-Nhu et al., 2016; Tang et al., 2011). Notably, macro-scale analyses are limited, with most research concentrated on bays, estuaries, or medium-scale systems (Santos et al., 2021, 2022). Existing studies often concentrate on specific scales and a limited set of environmental variables, underscoring the need for comprehensive studies of coastal phytoplankton blooms to better understand marine ecosystems.

Phytoplankton blooms are influenced by multiple factors, and assessing the effect of a single factor, such as SST, does not fully capture the complexity of the processes involved. Multivariable coherence analyses, combining meteorological and climate factors, can provide deeper insights into these processes across temporal scales. The relationships between teleconnections and hydrological variables often exhibit non-linear behavior and scale-dependent oscillations, requiring analytical methods that address these complexities (Cannon, 2015; Gobena and Gan, 2013; Wu et al., 2006).

Wavelet transform coherence (WTC) analysis and cross-wavelet spectral analysis are approaches used widely for the simultaneous analysis of two signals in the frequency and time domains. These techniques have been applied to examine phenological changes at multiple temporal scales (Detto et al., 2018) and the teleconnections between phytoplankton blooms and large-scale climate indices (Blauw et al., 2018; Xiao et al., 2019; Liu et al., 2024). To extend the two-variable relationship to a multivariate relationship, multiple wavelet coherence (MWC) was developed by Hu and Si (Hu and Si, 2016). MWC can untangle a range of multivariate relationships by identifying spatial or temporal scale relationships and determining the proportion of variance in a response variable explained by predictor variables at specific scales. For example, Hu et al. used bivariate wavelet coherency and MWC to explore the spatial scale and location-dependent multivariate relationships between soil water content and environmental factors in a hummocky landscape in North America (Hu et al., 2017). Their study showed that MWC is an effective method for untangling the complex spatial and temporal variability associated with multiple controlling factors at multiple scales. Examining the coupling relationships between climate factors, meteorological variables, and phytoplankton blooms across temporal scales provides valuable insights. Understanding these scale-specific interactions is essential for improving predictions of coastal phytoplankton blooms. Identifying dominant factors at different scales can enhance the accuracy of data-driven statistical models and hybrid dynamical-statistical models used in coastal ecosystem research (Liu et al., 2023).

To improve our understanding of the coastal phytoplankton blooms, this study focused on marine scale and applied multivariable methods to analyze the relationships between phytoplankton blooms, climate oscillation signals, and various meteorological environments. First, the continuous wavelet transform (CWT) is applied to detect temporal patterns in the phytoplankton blooms, and the variation in annual and monthly phytoplankton blooms is calculated. Second, the WTC between phytoplankton blooms and each predicting factor is calculated. Third, the MWC between phytoplankton blooms and every combination of two or more factors is determined. Finally, the proportion of variance explained by each factor is compared to identify dominant drivers.

2. Materials and methods

2.1 Study area and data sources

2.1.1   Study area

The study area is located in the Northwest Pacific region, with large marine ecosystems (LMEs) as the unit of study, and the spatial scale of the study is defined in terms of marine area, which provides the possibility of establishing teleconnections between marine phytoplankton blooms and climatic and meteorological factors at larger spatial scales. Eight LMEs within the western North Pacific were studied, including the South China Sea (SCS), Sulu-Celebes Sea (SS), East China Sea (ECS), Yellow Sea (YS), Kuroshio Current (KC), Sea of Japan (SJ), Sea of Okhotsk (SO), and Oyashio Current (OC). LMEs encompass global coastal oceans and outer edges of coastal currents areas, which are defined by various distinct features of the oceans, including hydrology, productivity, bathymetry, and tropically dependent populations. Of the 66 LMEs identified globally, we chose the western North Pacific regions and examined eight LMEs. The latitude range of these eight LMEs includes 3°S–63°N, which can well reflect the latitudinal trends. The boundaries of LMEs were obtained from https://www.sciencebase.gov/catalog/item/55c77722e4b08400b1fd8244.

2.1.2   Phytoplankton blooms

To conduct a large-scale analysis of phytoplankton blooms, this paper uses the data products produced by the CIE-fluorescence algorithm proposed by Hou (Hou et al., 2022) and Dai (Dai et al., 2023), which can more accurately identify coastal phytoplankton blooms that are affected by green, yellow, brown, or even red phytoplankton by jointly inverting the remotely sensed reflectance of three visible bands (red, green, and blue) associated with these phytoplankton blooms. The phytoplankton blooms dataset (https://doi.org/10.5281/zenodo.7359262) covers a period from January 1, 2003, to December 31, 2020, with a spatial resolution of 0.01°. The pixel values within the data are classified into four categories: 0, 99, 100, and 255, representing no blooms, blooms, nodata, and areas masked out by land, clouds, or other factors, respectively.

We defined bloom intensity (BI, dimensionless) to represent the density of phytoplankton blooms for a month by integrating the bloom count and bloom-affected areas within 0.25° × 0.25° grid cells within that month while excluding the effect of nodata and masked areas in remote sensing interpretation. The equation for bloom intensity is as follows:

where $ {B}_{i} $ represents the enumerated blooms count for each 0.01° × 0.01° resolution pixel in one day within one 0.25° × 0.25° grid cell, while $ {N}_{i} $ represents the enumerated no blooms count for each 0.01° × 0.01° resolution pixel in one day within the same 0.25° × 0.25° grid cell, $ m $ is the number of original resolution pixels contained in the resampled grid cells; here the value is 625, and $ n $ is the number of days in a month.

To carry out the study of the phytoplankton blooms in the study areas, we spatially averaged the 216-month dataset by LMEs to obtain monthly BI data for these eight LMEs based on the BI dataset obtained from the previous dataset and definitions. These monthly BI data were used as the working database for this study to analyze the time series in the study areas. The average value of BI in the study area from January 2003 to December 2020 and BI original time series were shown as Fig. 1.

Figure  1.  Average value of BI in the study area from January 2003 to December 2020 and BI original time series—South China Sea (SCS), Sulu-Celebes Sea (SS), East China Sea (ECS), Yellow Sea (YS), Kuroshio Current (KC), Sea of Japan (SJ), Sea of Okhotsk (SO), Oyashio Current (OC).

DownLoad: Full-Size Img PowerPoint

2.1.3   Climate oscillation signals

To explore the teleconnection between climate oscillation and phytoplankton blooms, eight climate oscillation signal indices were selected. The Niño3.4 index, the SOI, and the MEI are representative indexes for the ENSO. The MEI is the time series of the leading combined empirical orthogonal function (EOF) of five different variables [sea level pressure (SLP), SST, zonal and meridional components of the surface wind, and outgoing longwave radiation (OLR)] over the tropical Pacific basin (30°S–30°N and 100°E–70°W) (Wolter and Timlin, 2011). The Niño3.4 index is the area-averaged SST from 5°S–5°N and 170°–120°W over the Pacific (Rayner et al., 2003). The SOI is defined as the normalized pressure difference between Tahiti and Darwin (Allan et al., 1991). The PDO is calculated from monthly SST anomalies poleward of 20°N in the Pacific basin by EOF analyses (Mantua and Hare, 2002). The Arctic Oscillation (AO) index is calculated as the projection of monthly mean 1 000 mb height anomalies onto the first empirical orthogonal function mode poleward of 20°N, using reconstructed data from the twentieth century (Higgins et al., 2000, 2002). The North Atlantic Oscillation (NAO) is calculated from Gibraltar, and SW Iceland is also given (Allan et al., 1991). The Atlantic Multidecadal Oscillation (AMO) is usually defined from the patterns of SST variability in the North Atlantic once any linear trend has been removed (McCarthy et al., 2015). The Dipole Mode Index (DMI) is the intensity of the Indian Ocean Dipole (IOD), represented by an anomalous SST gradient between the western equatorial Indian Ocean (50°–70°E and 10°S–10°N) and the southeastern equatorial Indian Ocean (90°–110°E and 10°S–0°N) (Saji and Yamagata, 2003).

Monthly MEI values for the same period of January 2003 to December 2020, as the index of climatic oscillation in this study, were downloaded from the NOAA website (https://psl.noaa.gov/enso/mei/). Monthly Niño3.4, SOI, PDO, AO, NAO, AMO, and DMI signals were taken from the Earth System Research Laboratory from the National Oceanic and Atmosphere Administration (http://www.esrl.noaa.gov/psd/).

2.1.4   Meteorological factors

Temperature and precipitation are important meteorological factors affecting phytoplankton growth (Dai et al., 2023; Trombetta et al., 2019). In this study, we mainly investigated the effects of atmospheric temperature, sea surface temperature, and precipitation on phytoplankton blooms, and to explore the ability of their effects, we constructed sixteen meteorological indices based on the three factors, as shown in Table 1. The original data was from ERA5 and downloaded from the Climate Data Store (CDS) (10.24381/cds.adbb2d47). Basic data include sea surface temperature (SST), 2 m temperature (t2m), and total precipitation (prec). The temperature and precipitation datasets consist of hourly data, which were preprocessed to construct evaluation indices with a temporal resolution of one month.

Table  1.  Indices of temperature and precipitation extremes used in the LMEs

ID	Definition	Unit
SST1	monthly mean value of daily mean SST	℃
SST2	monthly mean value of daily maximum SST	℃
SST3	monthly mean value of daily minimum SST	℃
SST4	monthly mean value of daily difference SST	℃
AT1	monthly mean value of daily mean t2m	℃
AT2	monthly mean value of daily maximum t2m	℃
AT3	monthly mean value of daily minimum t2m	℃
AT4	monthly mean value of daily difference t2m	℃
SSTAT	monthly mean value of daily difference between SST and t2m	℃
SSTM1	monthly count when SST1< 15℃	d
SSTM2	monthly count when 15 ℃ < SST1< 25℃	d
SSTM3	monthly count when SST1> 25℃	d
PREC	monthly mean value of daily mean precipitation	mm
PRECM1	monthly count when prec > 1 mm	d
PRECM2	monthly count when prec > 15 mm	d
PRECM3	monthly count when prec > 50 mm	d

 | Show Table

DownLoad: CSV

2.2 Methods

This study performed multiscale analyses of the individual and combined influences of climate indices and meteorological factors on coastal phytoplankton blooms. For the individual influence, the analysis was conducted for one teleconnection at a time on the entire dataset and on the datasets extracted according to the different phases of the teleconnections. For the combined influence, the analysis was conducted using two factors simultaneously or more factors simultaneously.

2.2.1   CWT

The CWT was performed to explore the dominant model patterns of variability and their characteristics of variation with time by decomposing a time series over a temporal-scale space (Charlier et al., 2015). Applying CWT decomposes the time series into all possible and continuous scales and produces a two-dimensional wavelet spectrum that reveals the temporal evolution and variability of each periodicity (Grinsted et al., 2004; Torrence and Compo, 1998). The Morlet wavelet, a commonly used wavelet in hydrological studies, was used in this study for its ability to adequately describe the shape of geoscience data (Labat, 2005, 2006). Furthermore, it has a better frequency resolution than other wavelets. The Morlet wavelet can be expressed as (Grinsted et al., 2004; Torrence and Compo, 1998):

where $ {\omega _0} = 6 $ is the dimensionless frequency for the Morlet wavelet due to the good balance between time and frequency localizations (Grinsted et al., 2004; Torrence and Compo, 1998). $\eta $ is dimensionless time. The CWT on a time series can then be written as (Grinsted et al., 2004):

where ${x_t}$ is the analyzed time series that is recorded in a discrete time sequence $(t)$ with a uniform interval of $\delta t$; and $s$ represents the scaling factor of the mother wavelet. The mother wavelet depends on a time variable, $\eta = s \cdot t$, which normalizes the CWT to have unit energy. This normalization allows all scales to be directly comparable to each other. Finally, the wavelet coefficients $ ({W_\psi }) $ of the CWT on a time series with the scaled and translated wavelet $\psi $ and a translation factor for the center of the window function $(\theta )$, is written as (Grinsted et al., 2004; Torrence and Compo, 1998):

where the asterisk (*) is the complex conjugate function. To correct the bias caused by the conventional CWT calculation does not include the inverse of the scale and an underestimation of energy in the high-frequency or lower-scale components occurs, the calculation of the wavelet power should include the inverse of the scale, which is done by dividing the conventional power by the corresponding scale (Liu et al., 2007). It can be presented as:

2.2.2   WTC

WTC can be used to determine the intensity of the covariance of two time series by analyzing the coherence of the CWT in time–frequency space. Given time series $X$ and $Y$, the wavelet coherence can be defined as (Torrence and Compo, 1998):

where $W_t^x(s)$ and $W_t^y(s)$ are the CWT of time series X and Y, respectively. $W_t^{xy}(s)$ is the crosswavelet spectrum and ${\boldsymbol{S}}$ is the smoothing operator, which can be defined as:

where ${{\boldsymbol{S}}_{{\mathrm{scale}}}}$ is the smoothing along the wavelet scale axis and $ {{\boldsymbol{S}}_{{\mathrm{time}}}} $ is the smoothing in time. For the Morlet wavelet, a suitable smoothing operator has been defined as (Torrence and Compo, 1998):

where $n{c_1}$ and $n{c_2}$ are normalization constants, which are determined numerically when the convolution processes are completed discretely; $\prod $ denotes the rectangle function, and 0.6 is an empirically determined scale decorrelation length for the Morlet wavelet.

2.2.3   MWC

MWC is similar to WTC, and it is also based on the auto- and cross wavelet power spectra among the analyzed variables. Assuming a response variable $Y$ and multiple predictor variables $X\;(X = \{ X_1,X_2,...,X_q\} )$, the MWC at scale $s$ and location $\tau $, that is, $\rho _m^2(s,t)$, can be written as follows:

where ${{\mathop {W}\limits^ \leftrightarrow} ^{y,x}}(s,t)$ is the matrix of the smoothed cross-wavelet power spectra between response variable $Y$ and explanatory variables $X$, ${{\mathop {W}\limits^ \leftrightarrow }^{x,x}}(s,t)$ is the matrix of the smoothed auto- and cross-wavelet power spectra among multiple explanatory variables $X$, ${{\mathop {W}\limits^ \leftrightarrow} ^{y,y}}(s,t)$ is the smoothed wavelet power spectrum of response variable $Y$, and ${{\mathop {W}\limits^ \leftrightarrow} ^{y,x}}{(s,t)^*}$ is the complex conjugate of ${{\mathop {W}\limits^ \leftrightarrow }^{y,x}}(s,t)$ (Hu and Si, 2016).

The wavelet phase between a response variable $Y$ and an explanatory variable ${X_1}$ is given as follows (Hu and Si, 2016):

where ${\text{Im}}$ and ${\text{Re}}$ denote the imaginary and real parts of ${{\mathop {W}\limits^ \leftrightarrow} ^{y,{x_1}}}(s,t)$, respectively.

2.2.4   Evaluation factor identifying

In this study, the ability of different climate oscillation signals and meteorological factors (or their combinations) to explain phytoplankton blooms variation at all scales was assessed by measuring the mean wavelet transform coherence (MWTC) at significant locations across all scales and times and the percent area of significant coherence (PASC) relative to the wavelet scale-location domain (outside the cone of influence) (Hu and Si, 2016). A greater average coherence with larger PASC indicates that more of the phytoplankton blooms variation is explained by a particular predictor variable case. We focused on all scales of phytoplankton blooms variation so that we could identify the factors underlying the variations in phytoplankton blooms. Sometimes, the average coherence increases with an increased number of independent variables, but the PASC does not necessarily increase (Hu and Si, 2016). Statistically, an increased PASC indicates that there is a significant increase in the phytoplankton blooms variation that can be explained at the 95% significant level. From a practical point of view, an additional factor is considered to be significant when it increases the PASC of at least 5% (Hu et al., 2017; Su et al., 2019).

3. Results

3.1 Temporal patterns of phytoplankton blooms

3.1.1   Multiple temporal scales of phytoplankton blooms

CWT was employed to examine the multi-scale spatial and temporal variability characteristics of phytoplankton blooms across different LMEs, shown as Fig. 2. Common features were observed in the wavelet patterns of phytoplankton blooms, with significant annual oscillations (approximately 12 months) evident across all phytoplankton bloom series throughout the study period. While many LMEs showed a continuous annual periodicity, other LMEs displayed intermittent breaks. For instance, the SCS showed a slight discontinuity in annual periodicity, whereas the SS showed more frequent breaks in annual periodicity. Additionally, some scattered significant periodicities were also revealed. Periodicities of around 6 months were found for the KC and the SJ. A strong periodicity of approximately 6 months was also observed for the SS from the 2012 to the 2018.

Figure  2.  Continuous wavelet transforms of the BI in eight western North Pacific LMEs. The period is measured in months. a. South China Sea; b. Sulu-Celebes Sea; c. East China Sea; d. Yellow Sea; e. Kuroshio Current; f. Sea of Japan; g. Oyashio Current; h. Sea of Okhotsk. Thick contours denote 5% significance levels against red noise. Pale regions denote the cone of influence where edge effects might distort the results. The color denotes the strength of wavelet power.

DownLoad: Full-Size Img PowerPoint

3.1.2   Variation in annual and monthly phytoplankton blooms

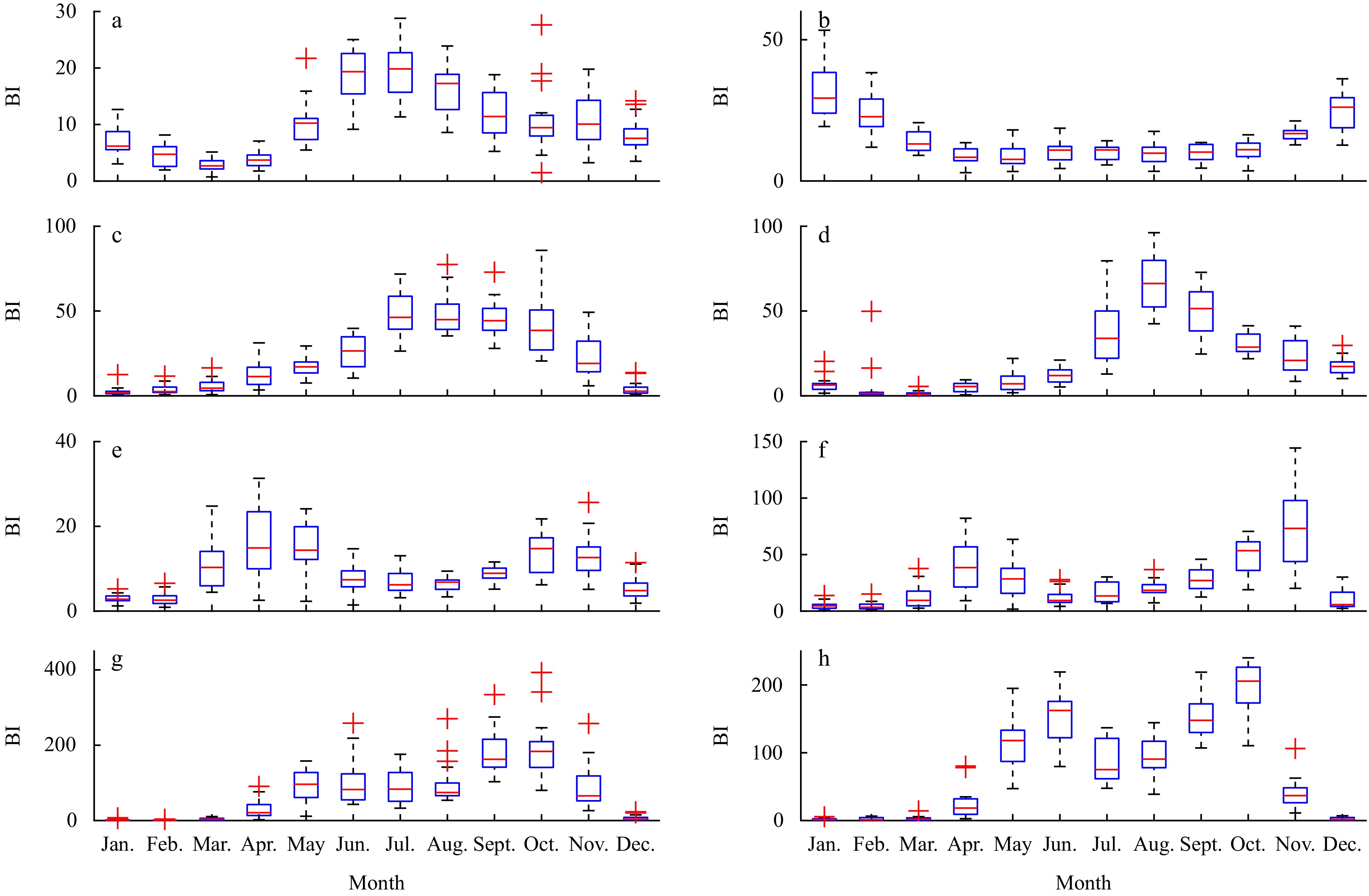
Given the significant annual oscillations observed in the CWT results for the bloom index (BI) series across different LMEs, the data were averaged monthly to investigate the patterns of change within the year. The temporal and spatial variations of phytoplankton blooms indicated by BI on monthly scales during the study period are shown in Fig. 3. It showed that the long-term monthly BI had a bimodal trend on KC, SJ, OC, and SO, with one peak in spring (April, April, May, and June, respectively) and the other in autumn (September, November, October, and October, respectively). These regions displayed typical seasonal characteristics of both spring and autumn blooms. In contrast, the BI on SCS, ECS, and SJ were concentrated primarily in July and August, reflecting summer blooms, which suggest that elevated temperatures during these months promote phytoplankton growth. Meanwhile, the highest peaks of SS occurred in winter (January), indicating a winter bloom pattern, where cooler temperatures appear to inhibit phytoplankton growth.

Figure  3.  Box-plots of month BI over the study period on eight LMEs. a. South China Sea; b. Sulu-Celebes Sea; c. East China Sea; d. Yellow Sea; e. Kuroshio Current; f. Sea of Japan; g. Oyashio Current; h. Sea of Okhotsk. The midline in the boxplots is the median, the upper and lower boundaries of the box are the interquartile range, and the red crosses are the outliers.

DownLoad: Full-Size Img PowerPoint

3.2 Individual factor controlling phytoplankton blooms variability

The effects of individual factors on variations in phytoplankton blooms are summarized in Tables 2 and 3. To highlight the most important factors for each LMEs, the climate oscillation signals with the highest MWTC and PASC are shown in bold, and the meteorological factors with the highest MWTC and PASC are shown in bold and italic. The results showed that the mean and highest values of MWTC and PASC for the meteorological signals are significantly higher than the values of MWTC and PASC for the climate oscillation signals. This finding aligns with the fundamental mechanisms by which climate oscillations affects phytoplankton growth and reproduction through the teleconnection that influence meteorological conditions, such as precipitation and temperature, and subsequently alter the physicochemical properties of the region.

Table  2.  MWTC between BI and individual factors

Factor	SCS	SS	ECS	YS	KC	SJ	OC	SO
MEI	0.2729	0.3899	0.3552	0.2939	0.2766	0.3471	0.2504	0.2997
SOI	0.2681	0.3557	0.3809	0.2085	0.2471	0.3312	0.2669	0.2612
Niño3.4	0.5535	0.6278	0.5200	0.4975	0.5509	0.5315	0.4592	0.4822
PDO	0.3569	0.5311	0.4973	0.4167	0.3908	0.3326	0.3261	0.3532
AO	0.2509	0.2881	0.2512	0.2340	0.3886	0.2669	0.2012	0.3485
NAO	0.3250	0.3660	0.3163	0.2930	0.2722	0.3417	0.2392	0.3348
AMO	0.4632	0.5933	0.5355	0.5096	0.3647	0.4814	0.4236	0.5149
DMI	0.3275	0.3041	0.2240	0.2616	0.2848	0.3223	0.2628	0.2922
SST1	0.7640	0.8855	0.6930	0.6632	0.3701	0.5103	0.7134	0.6361
SST2	0.7734	0.8871	0.6906	0.6669	0.3700	0.5049	0.7082	0.6254
SST3	0.7535	0.8830	0.6938	0.6600	0.3705	0.5156	0.7168	0.6467
SST4	0.4006	0.2925	0.4444	0.5369	0.4829	0.4226	0.4318	0.6699
AT1	0.7374	0.7478	0.6607	0.6159	0.3483	0.6010	0.6654	0.6658
AT2	0.752	0.7688	0.6601	0.6127	0.3573	0.6045	0.6414	0.6520
AT3	0.7194	0.7119	0.6597	0.6180	0.3363	0.5918	0.6834	0.6777
AT4	0.8711	0.7725	0.6111	0.6175	0.4164	0.4034	0.5152	0.6550
SSTAT	0.6546	0.7932	0.7675	0.6718	0.5824	0.6120	0.5497	0.6761
SSTM1	0.3659	NA	0.5839	0.6360	0.3626	0.5974	0.8028	0.7665
SSTM2	0.7422	0.3082	0.7107	0.7289	0.5743	0.5793	NA	NA
SSTM3	0.7979	0.7201	0.7578	NA	0.5326	NA	NA	NA
PREC	0.7338	0.7836	0.6187	0.7709	0.4180	0.4753	0.4446	0.5899
PRECM1	0.7410	0.8258	0.4312	0.7500	0.5337	0.4379	0.5797	0.7396
PRECM2	0.7171	0.7442	0.6704	0.7116	0.4611	0.5417	0.4030	0.5838
PRECM3	0.4725	0.5876	0.6038	0.6766	0.2839	0.5219	0.4551	0.4766
Note: Entries in bold indicate the climate oscillation signals with the highest coherence. Entries in bold and italic indicate the meteorological factors with the highest coherence. The NA values indicate that these factors are highly correlated with other variables in the LMEs.

 | Show Table

DownLoad: CSV

Table  3.  PASC (%) for the wavelet transform coherence between BI and individual factors

Factor	SCS	SS	ECS	YS	KC	SJ	OC	SO
MEI	6.06	15.70	5.15	4.84	4.73	10.46	5.88	8.52
SOI	5.83	13.12	13.03	2.44	2.38	13.13	7.36	6.78
Niño3.4	27.72	33.16	21.32	16.89	26.59	23.10	18.97	20.44
PDO	12.68	26.41	16.25	15.95	15.46	10.10	10.32	12.07
AO	3.71	7.89	7.20	4.36	10.75	6.03	2.85	11.99
NAO	8.88	13.73	8.05	6.67	7.33	10.24	5.63	11.22
AMO	21.61	31.18	22.90	22.39	14.33	18.34	17.86	19.93
DMI	10.04	7.61	3.26	4.61	7.75	6.56	4.59	5.25
SST1	38.69	47.23	32.04	30.76	14.07	22.14	35.76	27.89
SST2	39.37	47.85	31.81	30.75	14.05	22.11	34.98	27.54
SST3	38.22	46.32	32.19	30.70	14.07	22.05	36.09	28.13
SST4	15.40	7.69	16.89	23.24	19.07	19.96	18.35	30.64
AT1	37.55	38.33	30.12	26.15	13.30	30.26	29.85	30.42
AT2	38.34	39.58	30.68	26.70	13.40	30.14	28.75	28.86
AT3	36.17	36.07	29.49	25.56	12.18	30.36	30.32	31.33
AT4	46.80	42.59	26.50	24.68	16.06	15.59	22.66	28.99
SSTAT	31.33	45.17	36.03	29.56	31.55	29.52	27.18	32.00
SSTM1	11.99	NA	27.04	29.00	13.15	27.66	40.01	36.39
SSTM2	36.57	9.81	33.30	36.16	27.74	30.21	NA	NA
SSTM3	39.59	35.28	35.69	NA	24.96	NA	NA	NA
PREC	38.02	42.24	26.27	40.26	18.81	20.37	19.83	23.74
PRECM1	38.37	46.76	16.15	39.45	22.55	16.55	28.09	31.51
PRECM2	36.48	39.46	27.26	36.74	21.72	26.47	17.39	23.68
PRECM3	22.75	25.43	24.50	34.91	9.80	22.66	18.25	18.23
Note: Entries in bold indicate the climate oscillation signals with the highest coherence. Entries in bold and italic indicate the meteorological factors with the highest coherence. The NA values indicate that these factors are highly correlated with other variables in the LMEs.

 | Show Table

DownLoad: CSV

The MWTC results demonstrated covariability between phytoplankton blooms and climate oscillation signals. Niño3.4 was the dominant climate oscillation factor for many of the LMEs. It was the climate oscillation factor with the highest coherence for five phytoplankton bloom series with an average largest MWTC. AMO was next in importance, with the highest coherence for three phytoplankton bloom series. The situation was different for meteorological factors, except for SSTAT, which exhibits a dominant factor in three LMEs (ECS, KC, and SJ); the dominant factors are different in other regions, i.e., the dominant factors for SCS, SS, YS, OC, and SO, are AT4, SST2, PREC, SSTM1, and SSTM1, respectively. When it came to PASC, the situation was similar to MWTC. The highest PASC of climate factors ranged from 18.57% to 33.07% across all LMEs, with an average largest PASC of 24.385%. Niño3.4 was the dominant climate factor for six LMEs, and AMO was next in importance for two LMEs. The highest PASC of meteorological factors were different among LMEs. The dominant meteorological factors were similar to MTWC, and the highest PASC of meteorological factors ranged from 31.05% to 52.61% across all LMEs, with an average largest PASC of 43.67%. Overall, the MWTC and PASC results were the same for the best meteorological factor and climate oscillation signal in the LMEs, except for the best climate factor for SO, which was different in MWTC and PASC, reflecting the reliability of the assessment method.

To further explore the influence of dominant meteorological factors on phytoplankton bloom patterns in different LMEs, WTC was used to illustrate the correlation between optimal meteorological factors and phytoplankton blooms across various periods, as shown in Fig. 4. Continuous annual periodicities were found between meteorological factors and bloom intensity at SCS, SS, ECS, YS, OC, and SO on timescales of 8–16 months by about 0°, 180°, 325°, 325°, 0°, and 0°, respectively, whereas scattered annual periodicities were found at KC and SJ by about 325°. Scattered annual periodicities were found at all LMEs on timescales of 4–8 months. It is worth noting that there were interannual oscillations with time scales of more than 48 months in the LMEs at high latitudes, such as KC, SJ, OC, and SO.

Figure  4.  Wavelet transform coherence between BI and meteorological factors. a. South China Sea; b. Sulu-Celebes Sea; c. East China Sea; d. Yellow Sea; e. Kuroshio Current; f. Sea of Japan; g. Oyashio Current; h. Sea of Okhotsk. The period is measured in months. Each subplot shows the wavelet transform coherence between Bloom Intensity in a single LMEs and the individual meteorological factors that best explain Bloom Intensity variation in that LMEs. Thick contours denote 5% significance levels against red noise. Pale regions denote the cone of influence where edge effects might distort the results. Small arrows denote the relative phase relationship (in-phase, arrows point right; anti-phase, arrows point left). The color denotes the strength of coherence.

DownLoad: Full-Size Img PowerPoint

Similar to the dominant meteorological factors, the dominant climate oscillation signals also exhibit correlation characteristics with phytoplankton blooms on different time scales, as shown in Fig. 5. Scattered annual periodicities with complicated phase relationships were found between Niño3.4 and Bloom Intensity in SCS, SS, KC, SJ, OC, and SO on timescales of 4–8 months during the study period by about 270°, 225°, 45°, 0°, 270°, and 45°, respectively. Scattered annual periodicities with complicated phase relationships were found between Niño3.4 and Bloom Intensity on SS, KC, and SJ on timescales of 8−16 months during the study period by about 135°, 0°, and 225°, respectively. whereas continuous annual periodicities were found in SCS, OC, and SO by about 270°. Especially, significant positive interannual oscillations were found at timescales of 50–64 months on SS and KC, whereas interannual oscillations were found at timescales of 32–40 months on SJ and SO by about 270° in ECS; significant positive interannual covariance was detected between AMO and Bloom Intensity on timescales of 8–16 months and 28–40 months, whereas continuous annual periodicities were found by 90° during 2013–2020. In YS, significant covariance was detected between AMO and Bloom Intensity on timescales of 8–16 months and 55–64 months by about 0° and 270°, respectively.

Figure  5.  Wavelet transform coherence between BI series and climate oscillation signals. a. South China Sea; b. Sulu-Celebes Sea; c. East China Sea; d. Yellow Sea; e. Kuroshio Current; f. Sea of Japan; g. Oyashio Current; h. Sea of Okhotsk. The period is measured in months. Each subplot shows the wavelet transform coherence between Bloom Intensity in a single LMEs and the individual climate oscillation signal that best explains Bloom Intensity variation in that LMEs. Thick contours denote 5% significance levels against red noise. Pale regions denote the cone of influence where edge effects might distort the results. Small arrows denote the relative phase relationship (in-phase, arrows point right; anti-phase, arrows point left). The color denotes the strength of coherence.

DownLoad: Full-Size Img PowerPoint

3.3 Combined factors explaining phytoplankton blooms variability

Table 4 summarizes the combinations of meteorological factors that optimally explain variations in phytoplankton bloom variations, considering individual factors as well as two-factor and three-factor combinations. The average MWTC value at significant domains for all two-factor combination cases was 0.8424, higher than those of individual factors (0.7972). Among all the two-factor combinations, AT4 and SSTAT were the most common, being a composition of the best two factors for explaining phytoplankton bloom variation for seven LMEs. A comparison between the two-factor cases and individual-factor cases showed that the PASC increased for all LMEs and the MWTC increased for seven LMEs when two factors were combined. The seven LMEs, i.e., SCS, SS, ECS, YS, KC, SJ, and SO, showed an increase that was more than 5% and considered significant, calculating as 6.66%, 7.46%, 13.94%, 15.44%, 9.02%, 13.58%, and 17.39%. In these LMEs, the increases in PASC with two combined factors were due to oscillations with periodicity around more than 32 months (Figs 4 and 6). The combination of two factors explained a greater amount of Bloom Intensity variation at this periodicity than any single factor, and the additional factor was not correlated with the previous single factor at oscillations around more than 32 months. When it comes to MWTC, an increase occurred in seven LMEs. The main reason for the disagreement in the changes in MWTC results was that the additional variance explained by two factors at a particular periodicity and time was already accounted for by the single factors. The contribution from some factors was weakened by overlapping effects because of the collinearity among factors. Therefore, only an additional factor that can independently explain a fair amount of additional bloom intensity variability would make a significant contribution (Hu et al., 2017).

Table  4.  Coherence between BI and multiple meteorological factors

LMEs	Single factor	MWTC	PASC	Two factors	MWTC	PASC	Three factors	MWTC	PASC
SCS	AT4	0.8711	46.80	AT4-PRECM3	0.8821	53.46	AT4-PREC-PRECM2	0.9195	65.58
SS	SST2	0.8871	47.85	SST2-SSTM2	0.8881	55.31	SST2-AT4-SSTM2	0.9312	71.88
ECS	SSTAT	0.7680	36.03	SSTAT-PRECM2	0.8431	49.97	SSTAT-SSTM1-PRECM3	0.9126	65.45
YS	PREC	0.7709	39.45	AT4-SSTM3	0.8825	54.89	AT4-SSTM3-PREC	0.9527	69.04
KC	SSTAT	0.5824	31.55	AT4-SSTAT	0.7473	40.57	AT2-SSTAT-SSTM1	0.8652	57.78
SJ	SSTAT	0.6120	29.52	SSTAT-PRECM2	0.7752	43.10	SSTAT-SSTM1-PREC	0.8715	56.72
OC	SSTM1	0.8028	40.01	AT4-SSTM1	0.7820	41.86	AT4-SSTM1-PRECM2	0.8565	49.64
SO	SSTM1	0.7665	36.29	SSTAT-SSTM1	0.8765	53.68	AT3-SSTAT-SSTM1	0.9342	68.94

 | Show Table

DownLoad: CSV

Figure  6.  Two-factor multiple wavelet coherence. a. South China Sea; b. Sulu-Celebes Sea; c. East China Sea; d. Yellow Sea; e. Kuroshio Current; f. Sea of Japan; g. Oyashio Current; h. Sea of Okhotsk. The period is measured in months. Each subplot shows the multiple wavelet coherence between Bloom Intensity in a single LMEs and the best combination of two factors. Thick contours denote 5% significance levels against red noise. Pale regions denote the cone of influence where edge effects might distort the results. The color denotes the strength of coherence.

DownLoad: Full-Size Img PowerPoint

Likewise, when there were three predictor variables in the MWC analysis, all MWTC further increased to more than 0.85, with the PASC further increasing (Table 4 and Fig. 7). The average MWTC value at significant domains for all three-factor combination cases was 0.9034. A comparison between the three-factor cases and two-factor cases showed an increase on PASC that was more than 5% and considered significant. Compared to the insignificant increase in MWTC for two-factor relative to an individual factor, the increase in MWTC for three-factor relative to two factors was highly significant. This phenomenon suggests that the addition of a third factor diminishes the overlapping effect of the contributions of some of the factors.

Figure  7.  Three-factor multiple wavelet coherence. a. South China Sea; b. Sulu-Celebes Sea; c. East China Sea; d. Yellow Sea; e. Kuroshio Current; f. Sea of Japan; g. Oyashio Current; h. Sea of Okhotsk. The period is measured in months. Each subplot shows the multiple wavelet coherence between bloom intensity in a single LMEs and the best combination of three factors. Thick contours denote 5% significance levels against red noise. Pale regions denote the cone of influence where edge effects might distort the results. The color denotes the strength of coherence.

DownLoad: Full-Size Img PowerPoint

Similar to the optimally explained combinations of meteorological factors, Table 5 and Fig. 8 summarize the combinations of meteorological factors and climate oscillation signals that optimally explain phytoplankton bloom variations. Among all the combinations, AMO, Niño3.4, and SSTAT formed the most common optimal combination for explaining variations in phytoplankton blooms. The addition of the climate oscillation signal resulted in a significant increase in both average MWTC and PASC than single factors. However, the PASC on OC LMEs decreased by 1.49%. Similar to the above, part of the reason for the lack of PASC expansion was that most areas with a significant correlation between bloom intensity and the additional ocean signals were located within the area that already showed significant coherence for the best individual meteorological factor.

Table  5.  Coherence between BI and meteorological factor/climate oscillation signal combinations

LMEs	Combined factors	MWTC	PASC/%
SCS	AT4-AMO	0.8749	53.25
SS	SST3-AMO	0.9018	61.55
ECS	SSTAT-PDO	0.8201	48.26
YS	PREC-AMO	0.8129	45.50
KC	SSTAT-AO	0.7342	39.92
SJ	AT2-Niño3.4	0.7662	42.38
OC	AT3-Niño3.4	0.7717	38.52
SO	PREC-Niño3.4	0.8278	49.53

 | Show Table

DownLoad: CSV

Figure  8.  Meteorological factors/climate oscillation signals combination multiple wavelet coherence. a. South China Sea; b. Sulu-Celebes Sea; c. East China Sea; d. Yellow Sea; e. Kuroshio Current; f. Sea of Japan; g. Oyashio Current; h. Sea of Okhotsk. The period is measured in months. Each subplot shows the multiple wavelet coherence between Bloom Intensity in a single LMEs and the best meteorological factors/climate oscillation signals combination. Thick contours denote 5% significance levels against red noise. Pale regions denote the cone of influence where edge effects might distort the results. The color denotes the strength of coherence.

DownLoad: Full-Size Img PowerPoint

Overall, the optimal combination of climate oscillation factor/meteorological factor primarily enhanced the interannual cycle correlation at scales longer than 32 months in individual LMEs relative to the single best meteorological factor, while it mainly increases the correlation of the intra-annual cycle within 4–16 months, especially the semi-annual cycle correlation of 4–8 months, relative to the single best climate oscillation factor. This finding underscores the importance of incorporating large-scale climate oscillation signals into phytoplankton bloom prediction models alongside traditional environmental factors. This approach can help constrain model stability on larger scales, offering a more robust framework for predictive modeling in phytoplankton bloom studies.

4. Discussion

4.1 Meteorological factors driving phytoplankton blooms spatiotemporal patterns

The wavelet analyses results reveal variability in the optimal predictors contributing significantly to the explained variance across the eight LMEs within the study area. As one moves from the equator to higher latitudes, distinct combinations of the most influential predictors emerge, illustrating a nuanced geographical pattern. While certain similarities may exist between regions, it is crucial to acknowledge that the underlying mechanisms driving these patterns may differ, underscoring the intricate and region-specific nature of the factors governing marine ecosystem dynamics. This highlights the need for a tailored understanding of the contributing elements in each LMEs.

At low latitudes, AT4-PREC-PRECM2 was the best predictor for the SCS. This suggests that phytoplankton blooms in the SCS are primarily influenced by atmospheric temperature and precipitation, particularly the AT4. A significant positive correlation was observed between diurnal atmospheric temperature differences and phytoplankton blooms directly on an annual scale (Fig. 2). Increased diurnal temperature differences were found to enhance phytoplankton biomass, attributable to heightened photosynthesis during the day and reduced respiration at night, leading to increased organic matter accumulation (Jia et al., 2023; Villafañe et al., 2013). Moreover, precipitation exerted a significant influence on phytoplankton blooms in the SCS, with both PREC and PRECM2 contributing substantially to the explained variance. The meteorological factors related to SST did not appear in the combination of the best factors, suggesting that SST in the South China Sea region is a relatively weaker driver of phytoplankton bloom relative to the other meteorological factors.

SST2-AT4-SSTM2 was the best predictor combination for the SS. This suggests that phytoplankton blooms in the SS are more influenced by temperature, especially SST2. significant negative correlation between daily maximum SST and phytoplankton blooms directly on an annual scale (Fig. 2). This significant negative correlation suggests that temperature has become a major constraint on phytoplankton growth at SS and that a decrease in daily maximum temperature can significantly promote phytoplankton growth (Dang et al., 2020). The high correlation of daily maximum temperature compared to other factors under the SST factor also re-emphasizes the inhibitory effect of high temperature on phytoplankton growth and reproduction in these LMEs. In addition, the contribution of SSTM2 to the explained amount is thought to be higher due to the covariance of SSTM2 with SST2, which does not differ much from MWTC and PASC in the case of a single meteorological factor. In contrast, the increase of the higher contribution of AT4 to the explained volume once again emphasizes the role of diurnal temperature differences in low latitudes as a driver of phytoplankton blooms.

SSTAT-SSTM1-PRECM3 was the best predictor combination for the ECS. This result suggests that SSTAT dominates effects on phytoplankton blooms, and SSTM1 and PRECM3 can contribute to the amount explained significantly. Air-sea temperature differences lead to heat exchange between seawater and the atmosphere, creating a density gradient that affects water column stability and mixed layer depths (MLD) (Behrenfeld et al., 2006; Polovina et al., 2008). The variations in MLD subsequently impact the supply of nutrients to phytoplankton within the mixed layer, consequently influencing the growth of phytoplankton (Boyce et al., 2010; Henson et al., 2009). This interconnected process underscores the pivotal role of air-sea temperature differences in regulating marine ecosystem dynamics, particularly in shaping the conditions that govern phytoplankton development.

AT4-SSTM3-PREC was the best predictor combination for the YS. This result suggests that PREC dominates effects on phytoplankton blooms, and AT4 and SSTM3 can contribute to the amount explained significantly. Significant negative correlation between PREC and phytoplankton blooms directly on an annual scale (Fig. 2). The YS, as a relatively closed sea area with a small size and the presence of several large rivers injected into it, the precipitation process is often accompanied by inputs of nutrients from the terrestrial phase to promote phytoplankton growth (Shi et al., 2012; Xiao et al., 2024), but there is a certain time lag, which is consistent with the phase lag behind of the BI relative to the PREC at the annual scales in the WTC analyses (Fig. 2). SSTM1 was directly and significantly positively correlated with phytoplankton blooms when it comes to OC. Despite the relatively low nutrient levels in this region controlled by the Thousand Islands cold front, phytoplankton were more significantly suppressed by low temperatures.

At high latitudes, AT3-SSTAT-SSTM1 was the best predictor for the SO. The fact that all three components are temperature dependent and represent SST, air temperature, and air-sea temperature difference indicates that at high latitudes, low temperature is the greatest constraint on phytoplankton growth and demonstrates, once again, the collinearity between the different factors. However, in conjunction with the bimodal phenomenon in Fig. 3, the dominant phytoplankton in the SO also showed considerable sensitivity to high temperatures due to interspecies differences (Okunishi et al., 2005), where increased summer temperatures inhibit phytoplankton growth and reproduction.

In summary, phytoplankton blooms showed strong temporal multiscale correlations with meteorological factors, particularly at high frequencies (i.e., short periods). Due to the multiple scale characteristics of phytoplankton blooms and related environmental variables, single factors can fail to capture the complex processes involved. The best predictors of phytoplankton blooms varied across LMEs, with the most common and important component being SSTAT. However, its mechanism of action varies among LMEs. In some LMEs, the explained variance increased with additional factors, while in others, it decreased. The differences arise from variations in latitudes, current influence, interspecific differences, and collinearity among the factors. These insights provide a new understanding of phytoplankton blooms on large scales, highlighting the variability of driving effects between scales.

4.2 Climate oscillations coupling phytoplankton blooms spatiotemporal patterns

Meteorological factors show a clear drive with phytoplankton in short cycles, while climate oscillations act as large-period factors and exhibit a good coupling with phytoplankton blooms. The results of the wavelet coherence analysis demonstrate the correlation of the BI in the eight LMEs, both for individual climate oscillation signals and a combination of climate oscillation/meteorological factors. While a uniform pattern of change is observed, significant regional variability exists, necessitating specific analyses for different LMEs.

At low latitudes, our results suggest that Niño3.4 is the most influential climate oscillation signal on phytoplankton bloom variation in SCS. This aligns with Siswanto’s work (Siswanto et al., 2017), which highlights the lagging and leading correlations of El Niño on phytoplankton biomass through the Niño3.4 Index. Interestingly, the AMO index, in conjunction with AT4, contributed more effectively to the explained variance when considering both meteorological factors and climate oscillation signals. It has been shown that the AMO and the pattern of cold/warm anomalies in the study area are closely related (Li and Bates, 2007; Wang et al., 2013). The positive AMO characterized by anomalous warm North Atlantic and cold South Atlantic leads to strong Southeast and East Asian summer monsoons (Lu et al., 2006), which is a potential driver to influence phytoplankton blooms. Despite its geographical distance from the Atlantic, phytoplankton blooms in SCS appeared more sensitive to influences from the AMO than from the ENSO when predicting phytoplankton blooms through a combination of climate and meteorological influences. This may be attributed to the dominance of ENSO in driving changes in meteorological conditions, such as precipitation and temperature, which directly affect phytoplankton growth, thereby diminishing the overlapping effect of contribution because of the collinearity between it and meteorological factors.

In SS, the situation is similar to SCS. Niño3.4 dominates as a single climate oscillation, while AMO becomes more influential when combined with meteorological factors. A similar phenomenon of overlapping effects reducing the degree of interpretation is shown in the ECS, where the non-dominant climate oscillation factor dominates the climate oscillation index/meteorological factor combination, AMO dominates when analyzed as a single climate oscillation index factor, and PDO dominates when combined with meteorological factors. The dominance of AMO in the YS, both when analyzed as a single oscillation factor and when participating in the combination of oscillation/meteorological factors, suggests that there is a significant pattern of teleconnection between AMO, as a large-scale general circulation phenomenon with global impacts, and regional geographic phenomena in the Northwest Pacific Ocean.

The KC, SJ, and OC are mainly controlled by ocean currents, and their internal phytoplankton blooms are more clearly affected by the effect of ENSO. In the WTC analysis (Fig. 4), the phase changes exhibited by both KC and SJ in 2014 and 2017 are well coupled with the ENSO phase transition from 2010–2012 strong double-peaked La Niña to 2014–2016 super-strong El Niño to 2016–2018 weak double-peaked La Niña in these two periods (Levine and McPhaden, 2016; Zheng et al., 2019). This is also consistent with the result that ENSO is the best factor in both regions regardless of whether it is analyzed as a single factor or a combined analysis with meteorological factors. When it comes to OC, there is a significant positive correlation between SSTM1 and phytoplankton blooms directly. Despite the relatively low nutrient levels in this region, which are controlled by cold currents, phytoplankton were more significantly suppressed by low temperatures. In the high latitude of SO, the situation is similar, showing significant phase changes in 2014 and 2017 and a dominant factor of Niño3.4 in all cases.

Overall, phytoplankton blooms and climate oscillation factors show strong temporal multiscale correlations, especially at low frequencies (i.e., long periods) relative to the meteorological factors, making the combination suitable for better complementarity. In addition to this, although both the mean MWTC and PASC of the combined climate oscillation/meteorological factor case are slightly smaller than those of the dual meteorological factor case, considering that the former may be preferred when information on certain meteorological factors is not available for a specific region. In addition, it is equally important to combine a non-dominant climate oscillation index factor with a dominant meteorological factor, considering the covariance between the dominant climate oscillation index and the dominant meteorological factor.

4.3 Limitation

Our study has some limitations. We studied globally recognized environmental variables. However, we did not consider some region-specific variables, such as the Madden-Julian Oscillation (MJO). The MJO is related to the interseasonal variability, influences on the tropical ocean, as well as tropical and extratropical weather and climate (Madden and Julian, 1972; Zhang, 2005; Zhang et al., 2020). It has been found that the MJO-related wind fields can induce the cooling and phytoplankton blooms off the South Vietnam coast in specific summers (Isoguchi and Kawamura, 2006). Additionally, we did not assess combinations of four or more factors. However, according to our results, there is a high chance that the PASC will decrease as more variables are taken into consideration. It is essential to acknowledge that the omission of nutrients from our wavelet analysis represents a limitation. Nutrients play a crucial role in influencing phytoplankton growth (Beardall et al., 2001; Van de Waal and Litchman, 2020), and their exclusion was a deliberate choice based on the study’s focus on examining the association between climate and meteorological factors. The study aims to discern the drivers and constraints imposed by climatic factors on meteorological elements, as well as the composite interplay between them, thus necessitating a specific scope that does not encompass nutrient salts in this context.

5. Conclusions

Temporal scale-dependent multivariate relationships between phytoplankton blooms, meteorological factors, and climate oscillation signals were identified in eight LMEs of the western North Pacific using WTC and MWC. Before conducting multivariate analysis, CWT was applied to detect temporal patterns in phytoplankton blooms. The CWT results revealed significant annual oscillations in the Bloom Intensity series across all regions during the study period. Some LMEs exhibited consistent annual periodicity, while others showed intermittent breaks. Oscillations with periodicities of 4 to 6 months were also detected in several LMEs. Seasonal climate patterns displayed single peaks or bimodal distributions, highlighting the temporal variability of phytoplankton blooms among the LMEs.

Comparing WTC and MWC analyses revealed that adding more explanatory factors generally improved the explanation of phytoplankton bloom dynamics. However, some declines in explanatory power were observed, likely due to collinearity among factors. The observed differences among LMEs stem from variations in latitude, ocean currents, species-specific traits, and the interplay of influencing factors. Meteorological factors primarily drove short-period changes in phytoplankton blooms, while long-period changes were more strongly linked to climate oscillations.

These findings offer novel perspectives for the formulation of early warning models for phytoplankton blooms, emphasizing the significance of incorporating non-dominant large-scale circulation indices alongside prevalent meteorological factors. It underscores the crucial role played by these less prominent indices in predicting the outcomes of phytoplankton blooms, thereby advocating for a comprehensive approach that considers a broader spectrum of influential factors. This approach underscores the crucial role that less prominent indices play in predicting phytoplankton bloom outcomes, advocating for a comprehensive strategy that considers a broader range of influential factors. Such an inclusive strategy has the potential to enhance the accuracy and reliability of predictions, offering a deeper understanding of the complex interplay between climatic and atmospheric drivers. Additionally, these findings contribute significantly to our knowledge of material-energy cycling in marine ecosystems, paving the way for further research in this field.