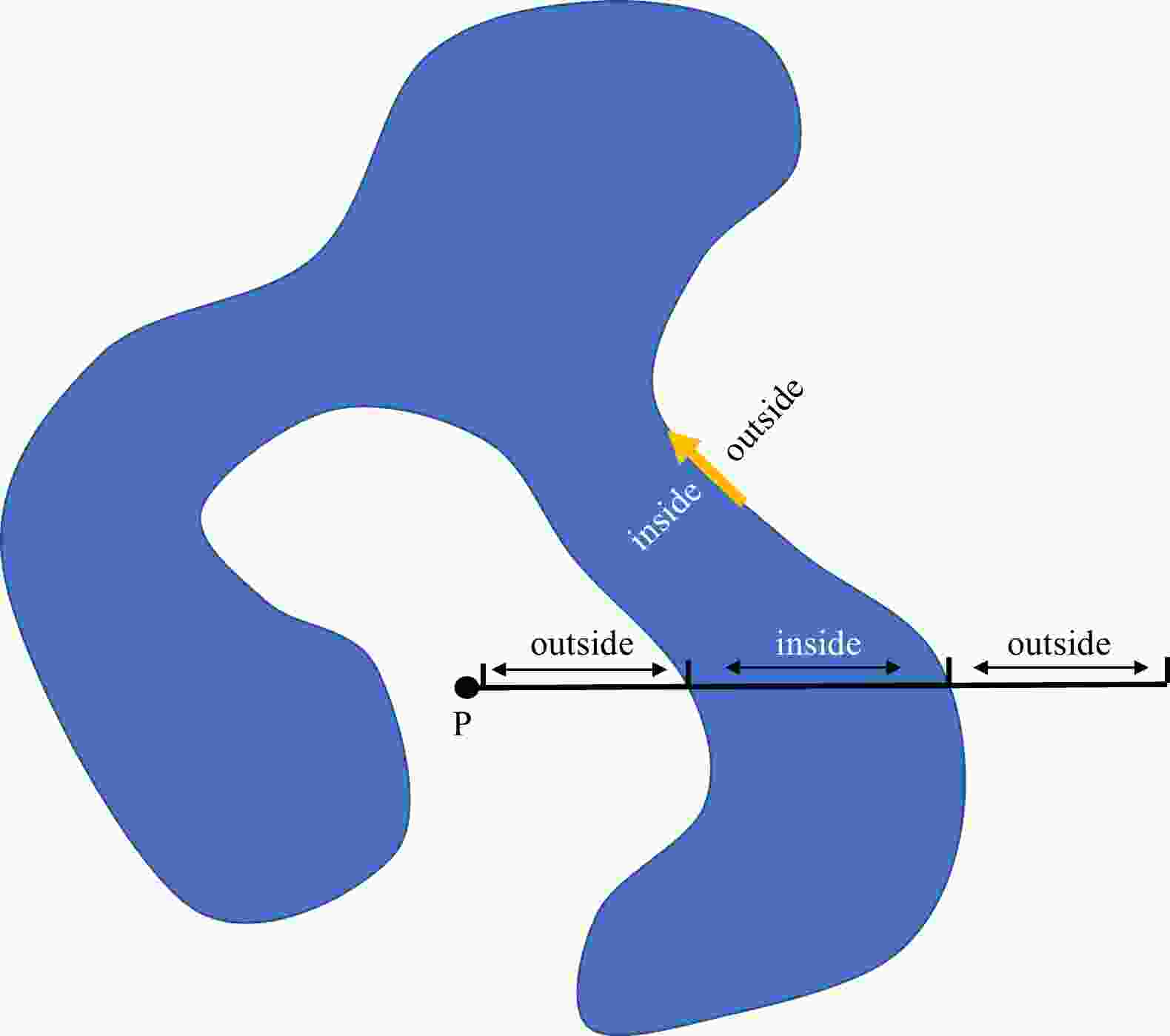
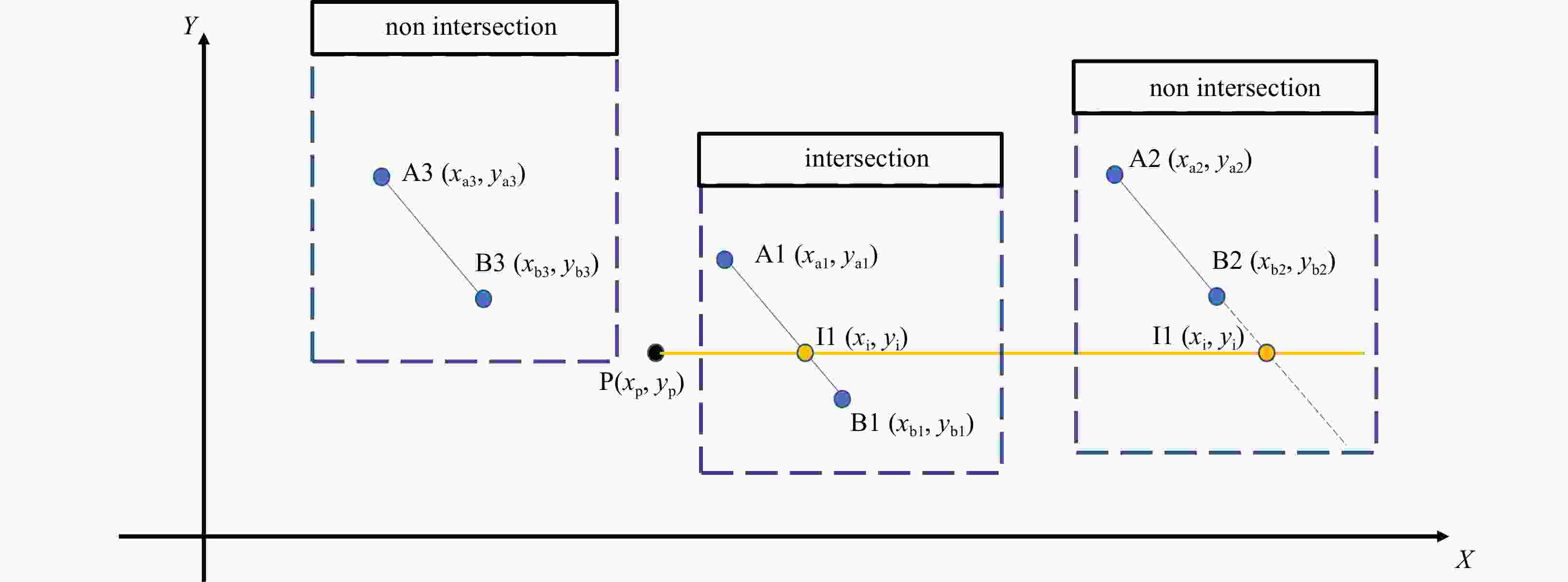
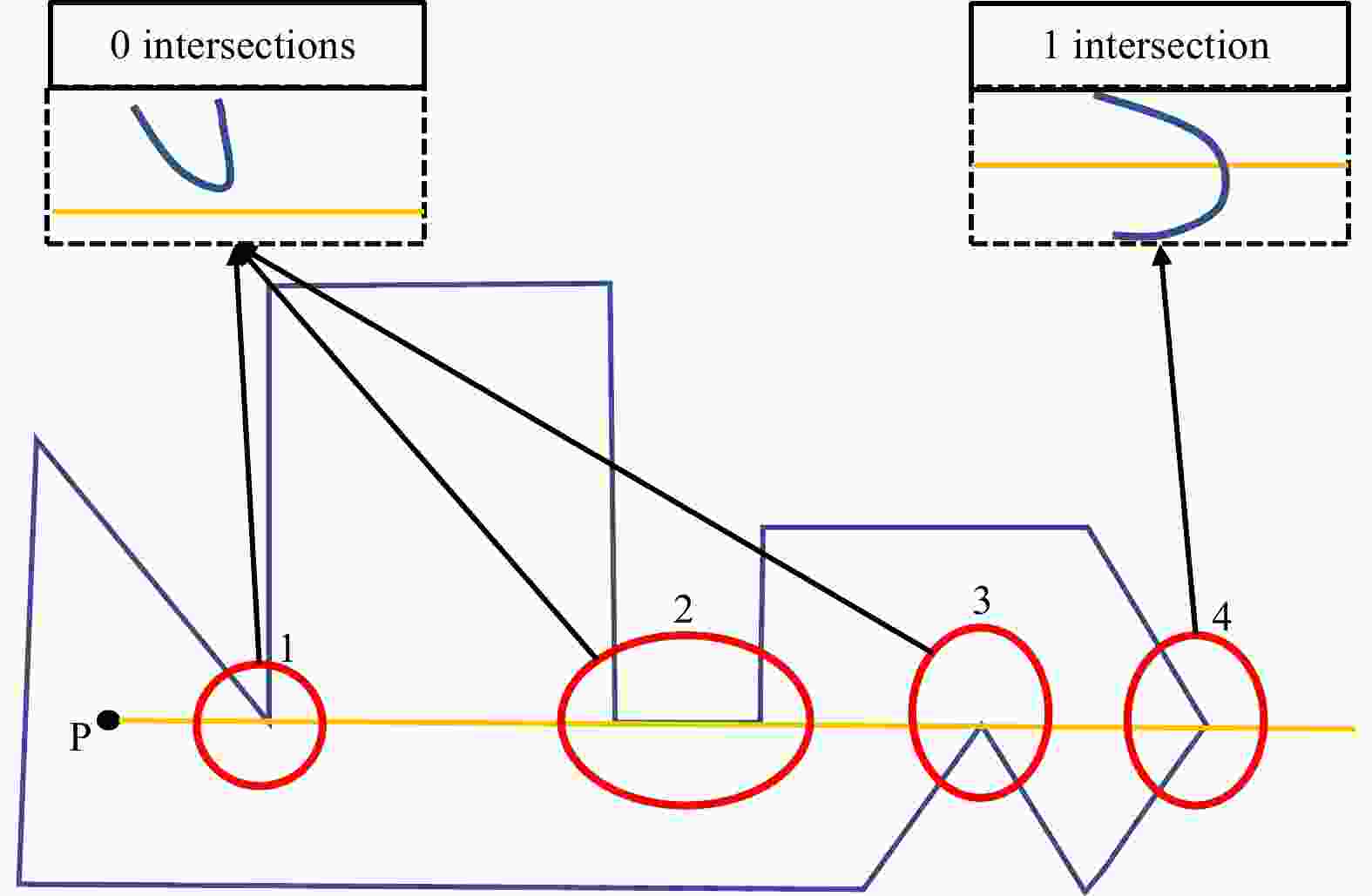
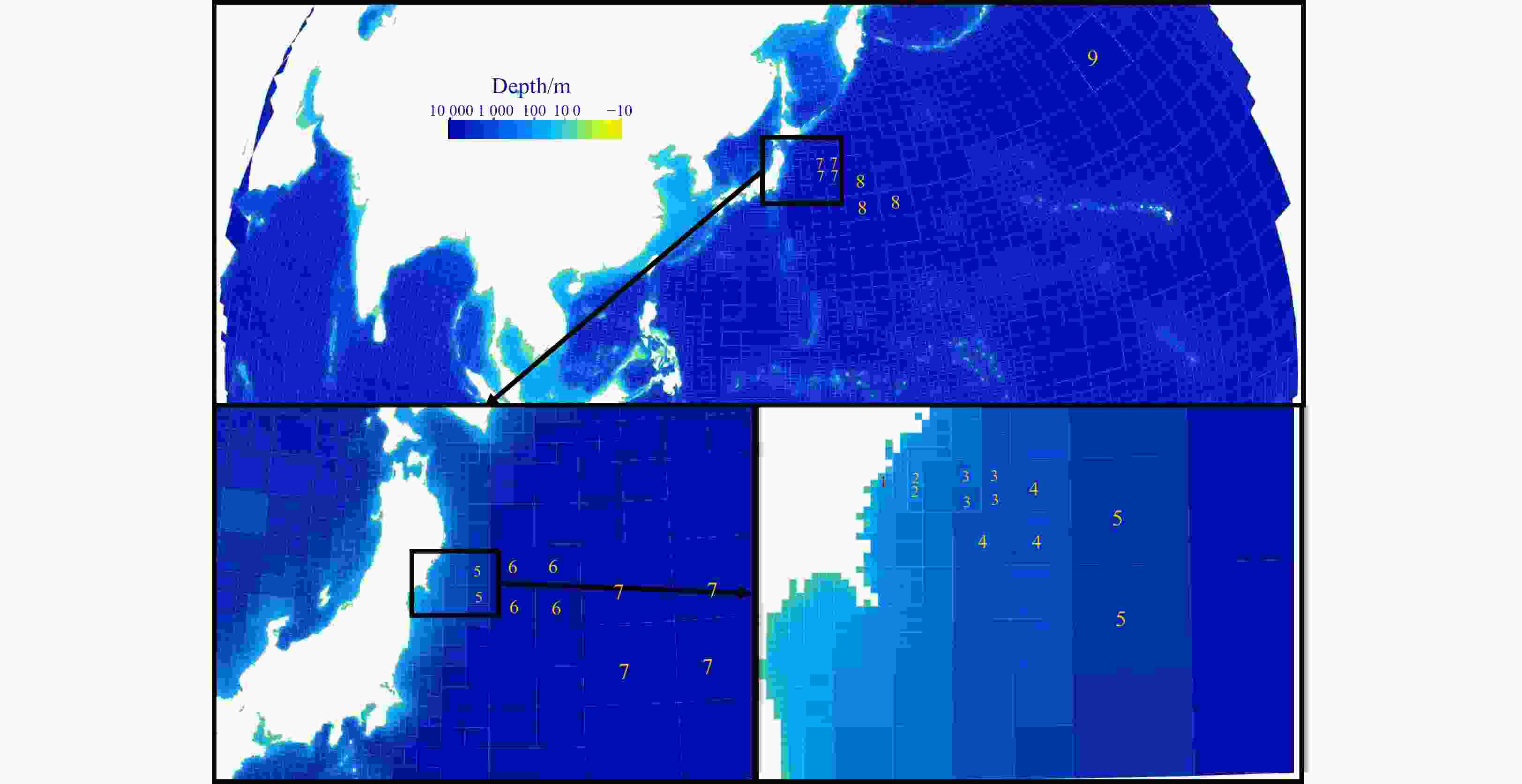
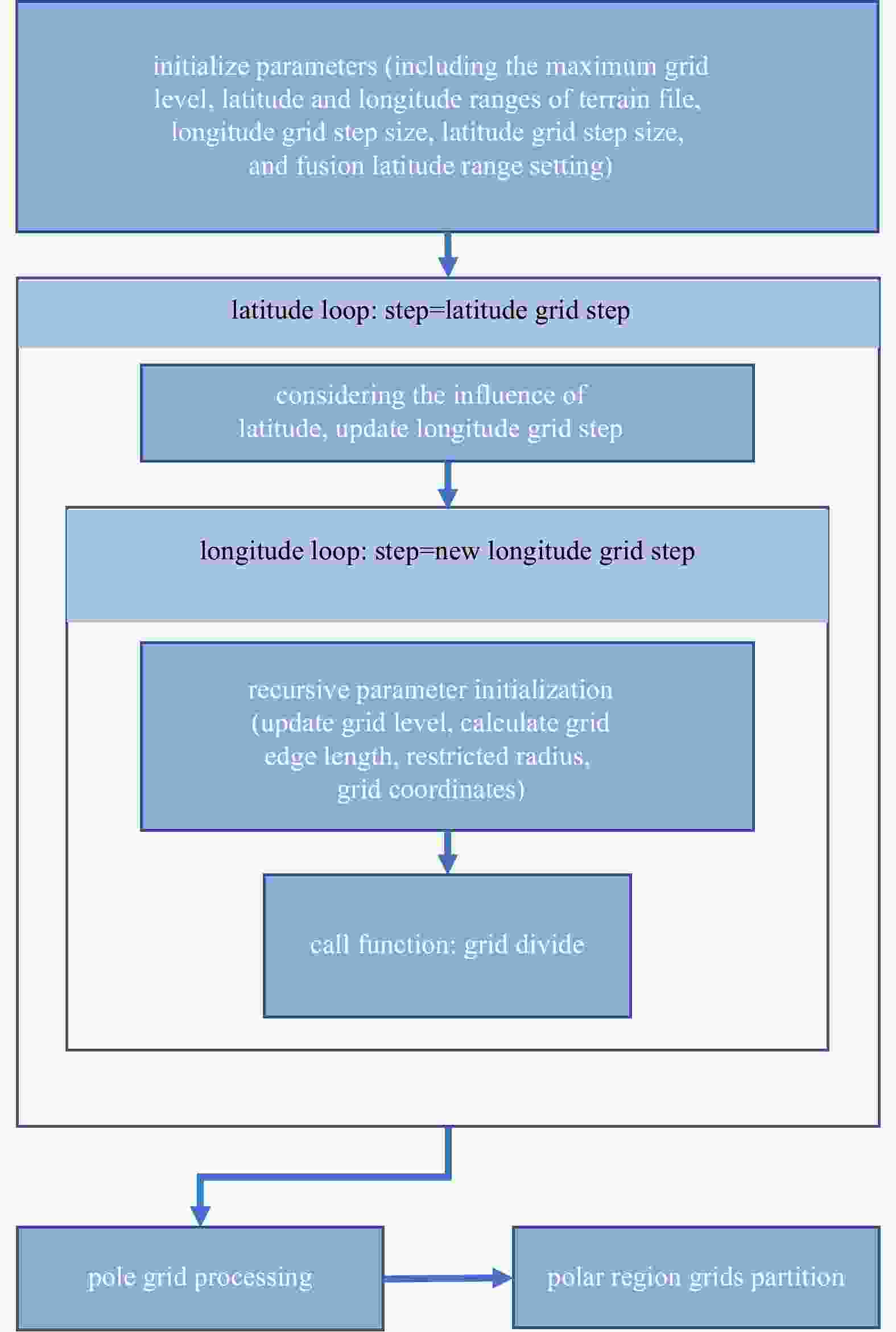
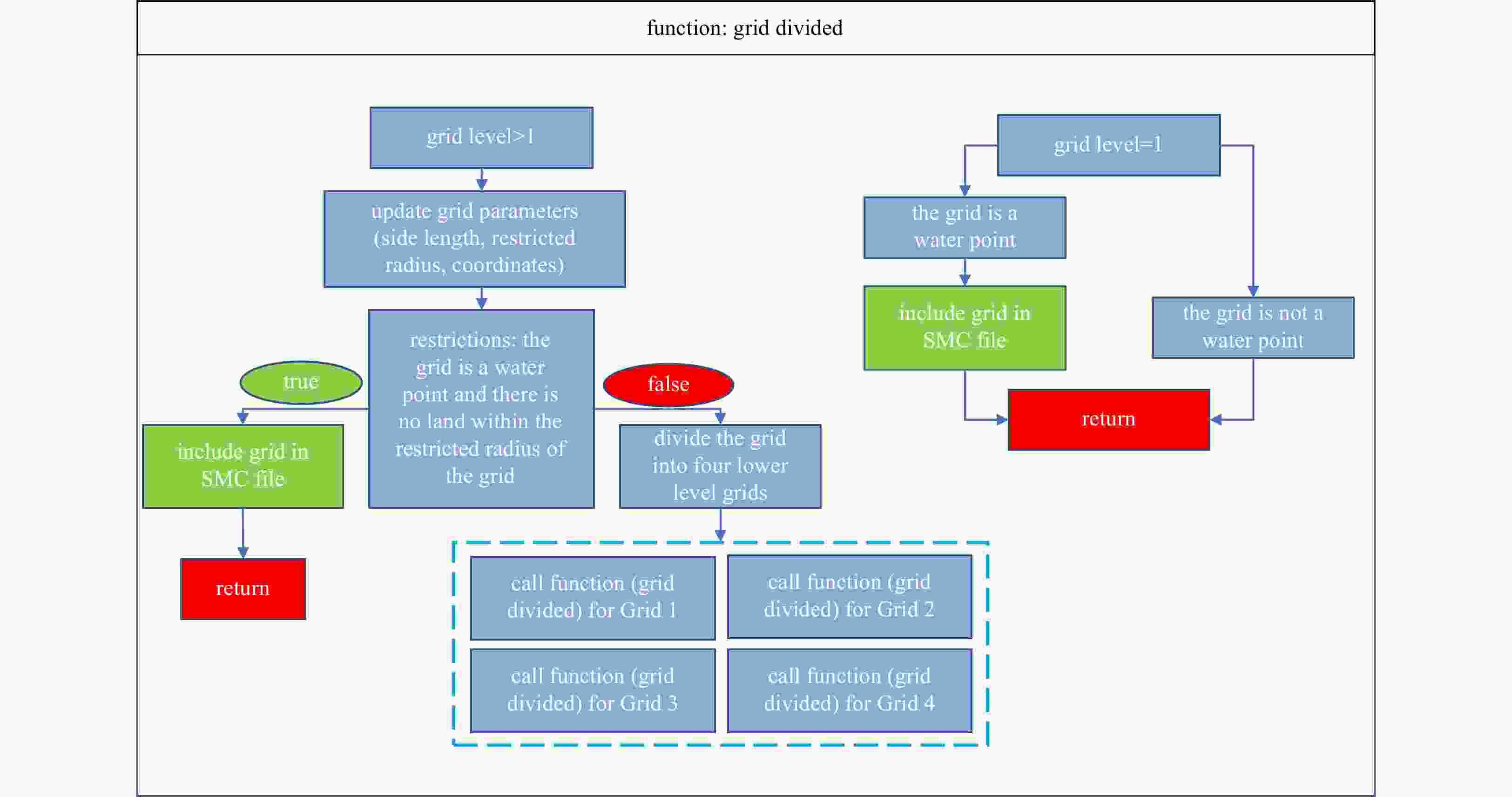
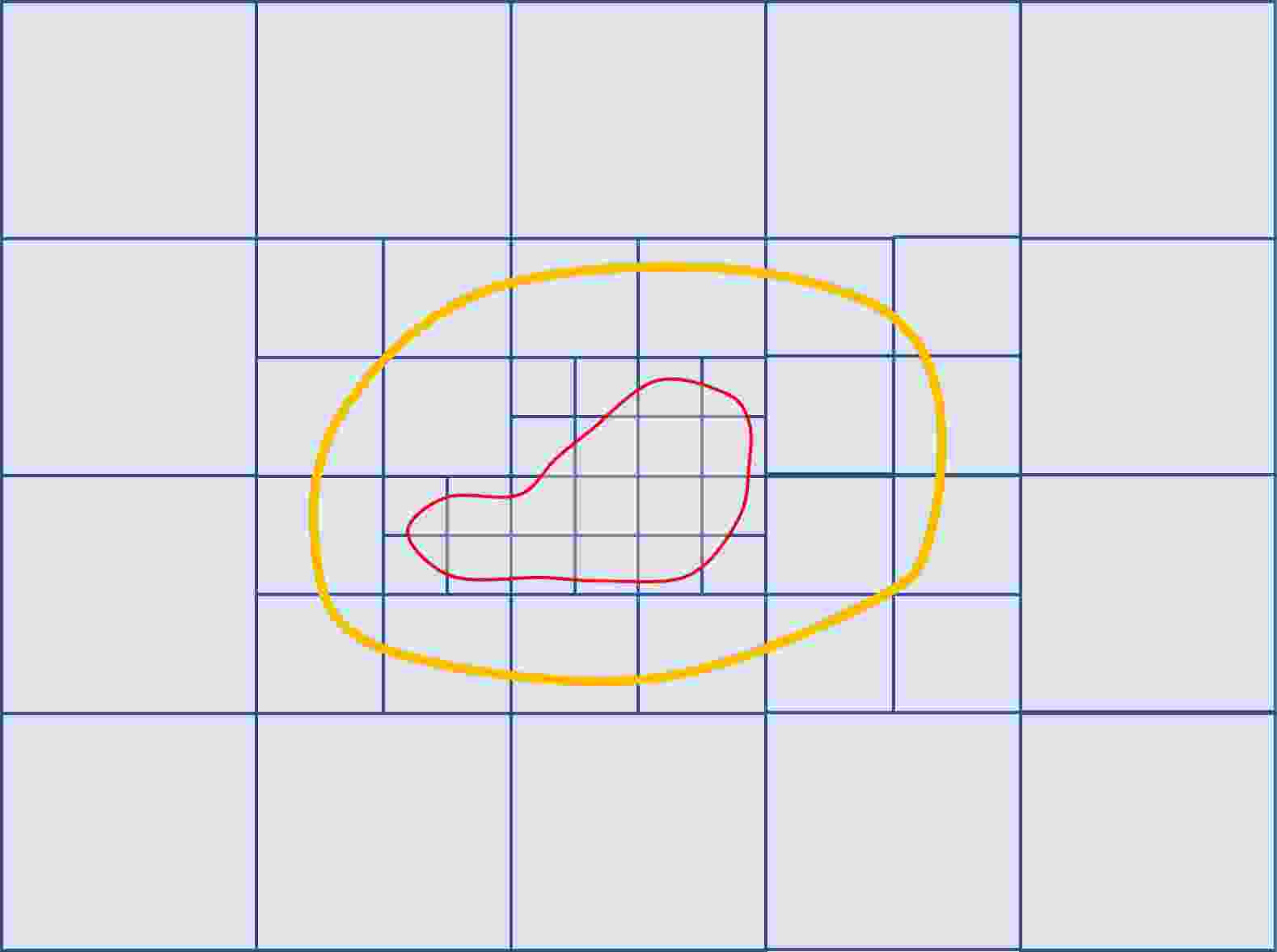
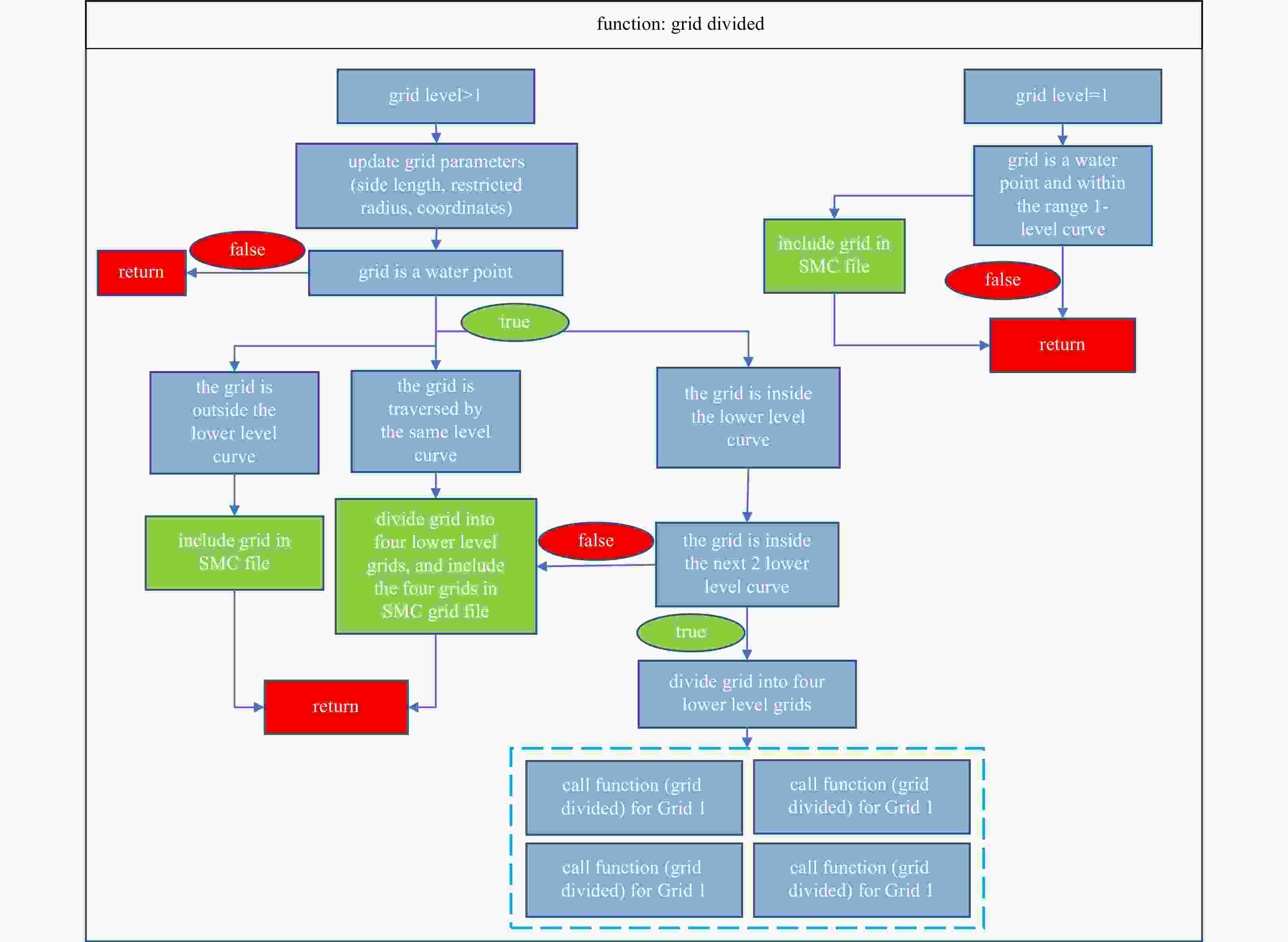
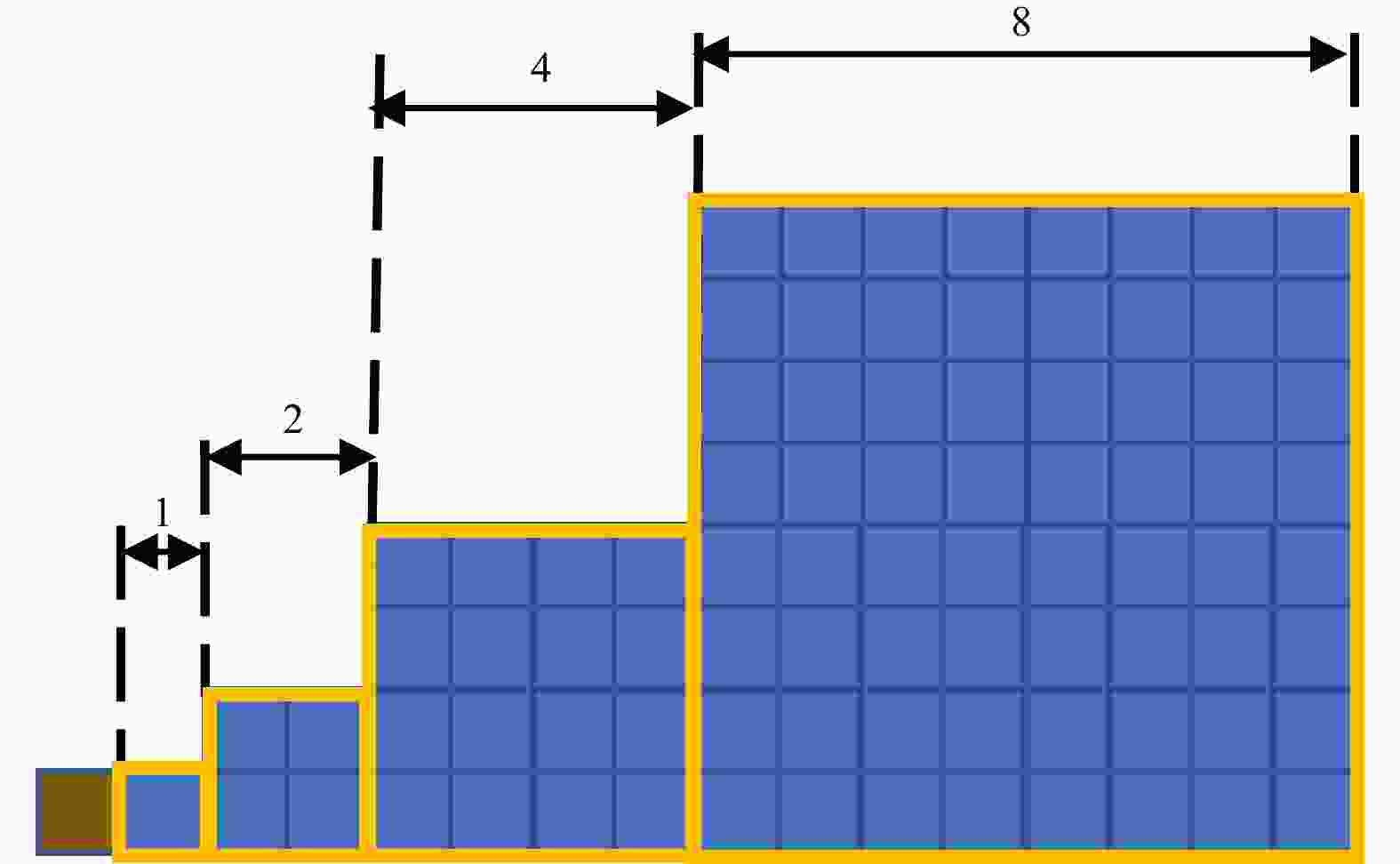
-
Abstract: This paper presents an efficient algorithm for generating a spherical multiple-cell (SMC) grid. The algorithm adopts a recursive loop structure and provides two refinement methods: (1) an arbitrary area refinement method and (2) a nearshore refinement method. Numerical experiments are carried out, and the results show that compared with the existing grid generation algorithm, this algorithm is more flexible and operable.
-
Key words:
- spherical multiple-cell grid /
- wave model /
- WAVEWATCH III /
- grid generation algorithm
-
Figure 10. A 6-level arbitrary area refined grid. a. The polygons used to specify the refined area, and b. the final generated grid.
Figure 12. The curves used to define the range of the mesh refinement (a), the curves used to delimit the nearshore and offshore refinement ranges (b), and corresponding (6-level) grid (c).
Figure 14. Wind field scatter on September 1, 2020 at 00:00 (a), 06:00 (b), 12:00 (c), and 18:00 (d).
Figure 15. Wind field scatter of typhoon center on September 1, 2020 at 00:00 (a), 06:00 (b), 12:00 (c), and 18:00 (d).
Figure 16. Significant wave heights on September 1, 2020 at 00:00 (a), 06:00 (b), 12:00 (c), and 18:00 (d).
Figure 17. Cumulative distribution of the characterization of energy on September 1, 2020 at 00:00 (a), 06:00 (b), 12:00 (c), and 18:00 (d).
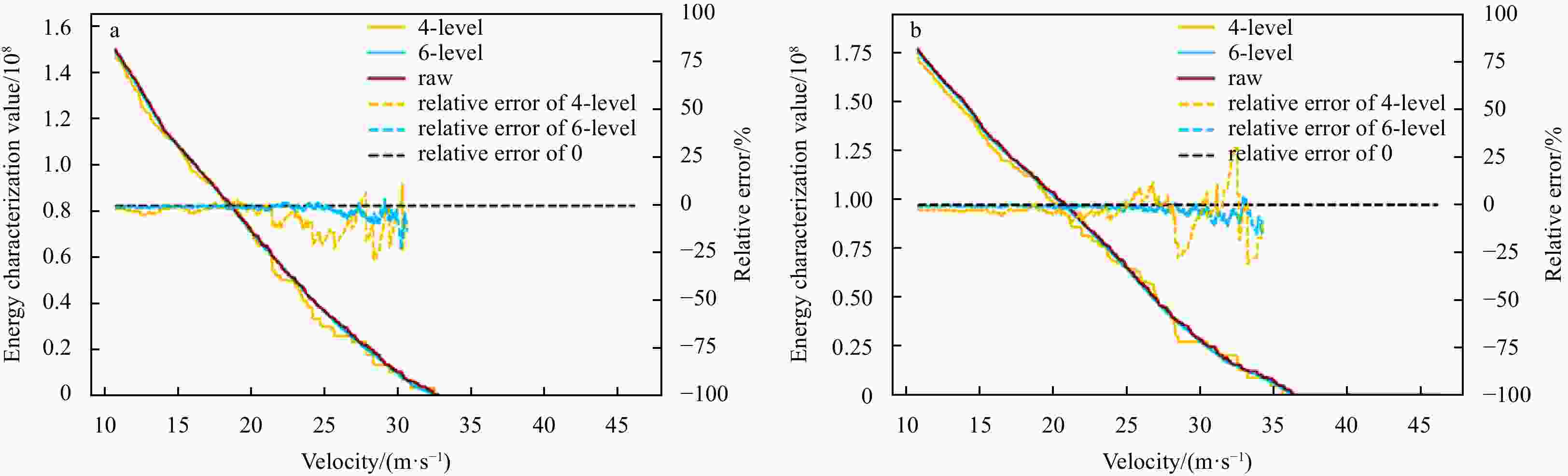
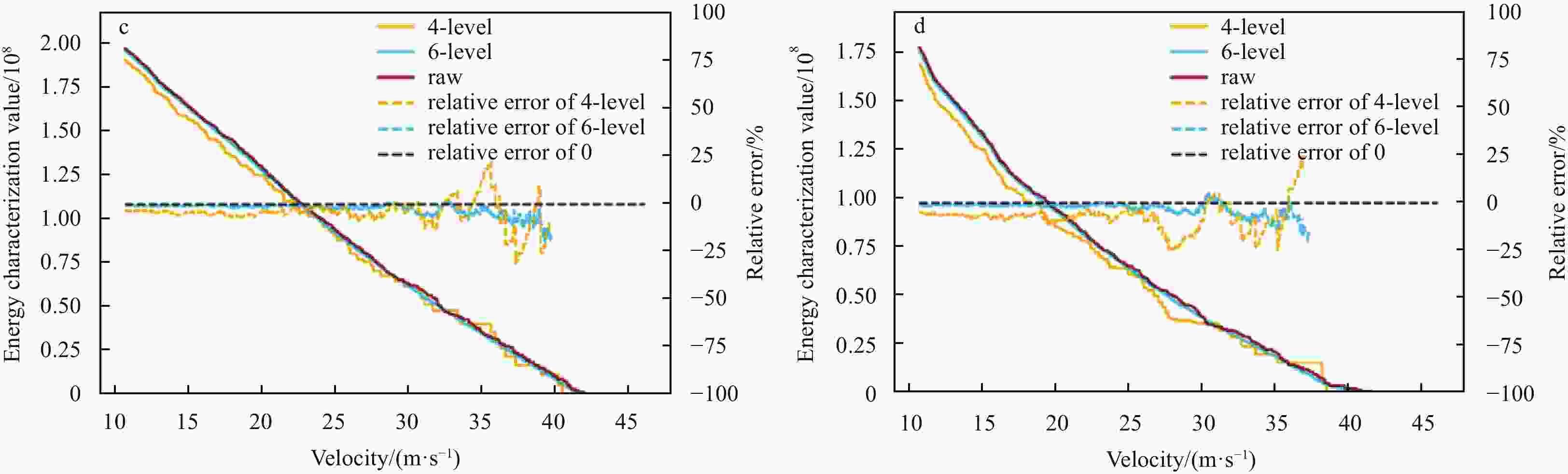
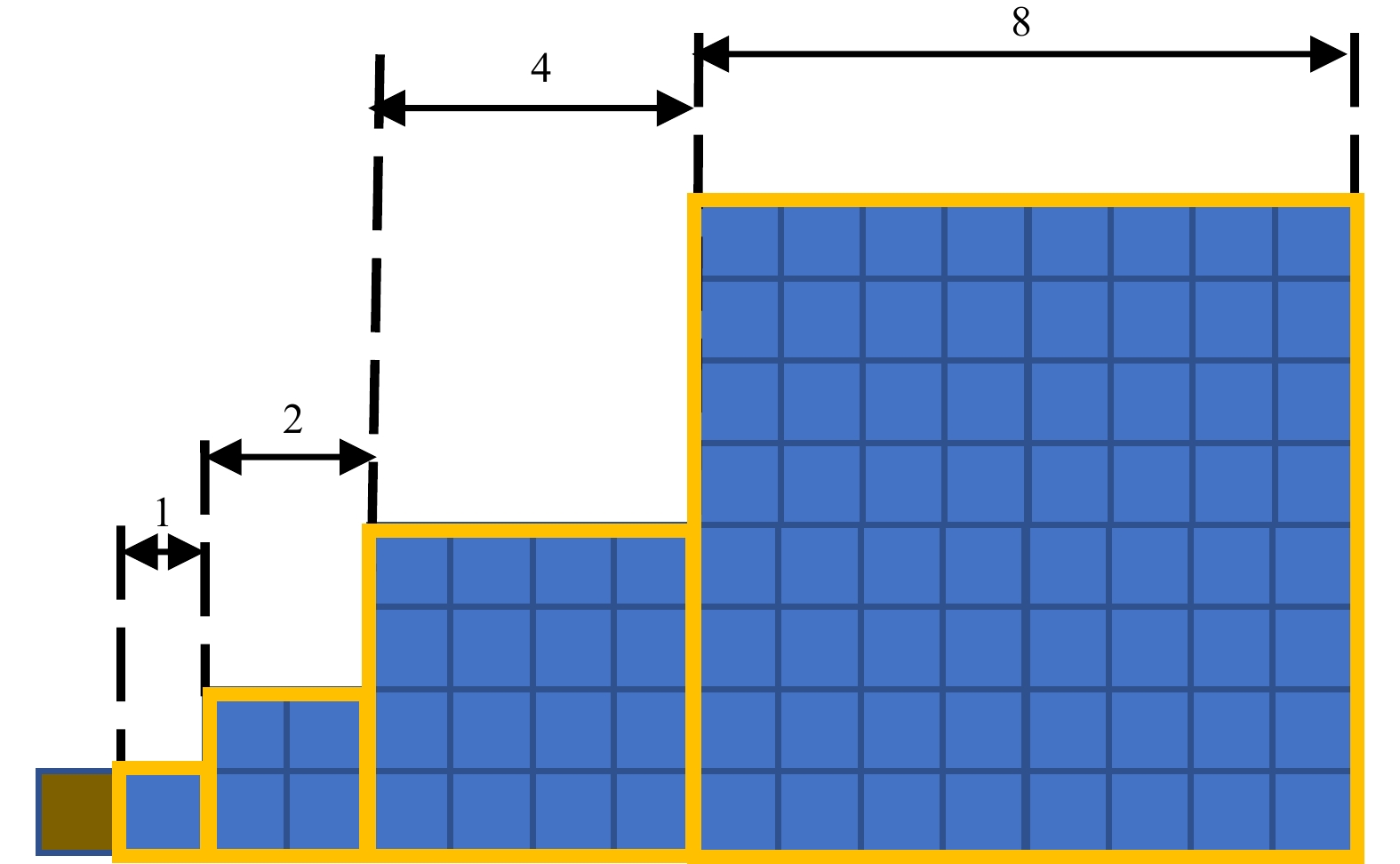
Table 1. Comparison of grid generation algorithms
Met Office Durrant and
SaulterThis paper Refinement method nearshore
refinementrectangular area refinement arbitrary area refinement and
nearshore refinementLevel of refinement fixed unfixed unfixed Degree of
completioncompleted under development completed 
下载: 导出CSV
Table 2. Resolution list
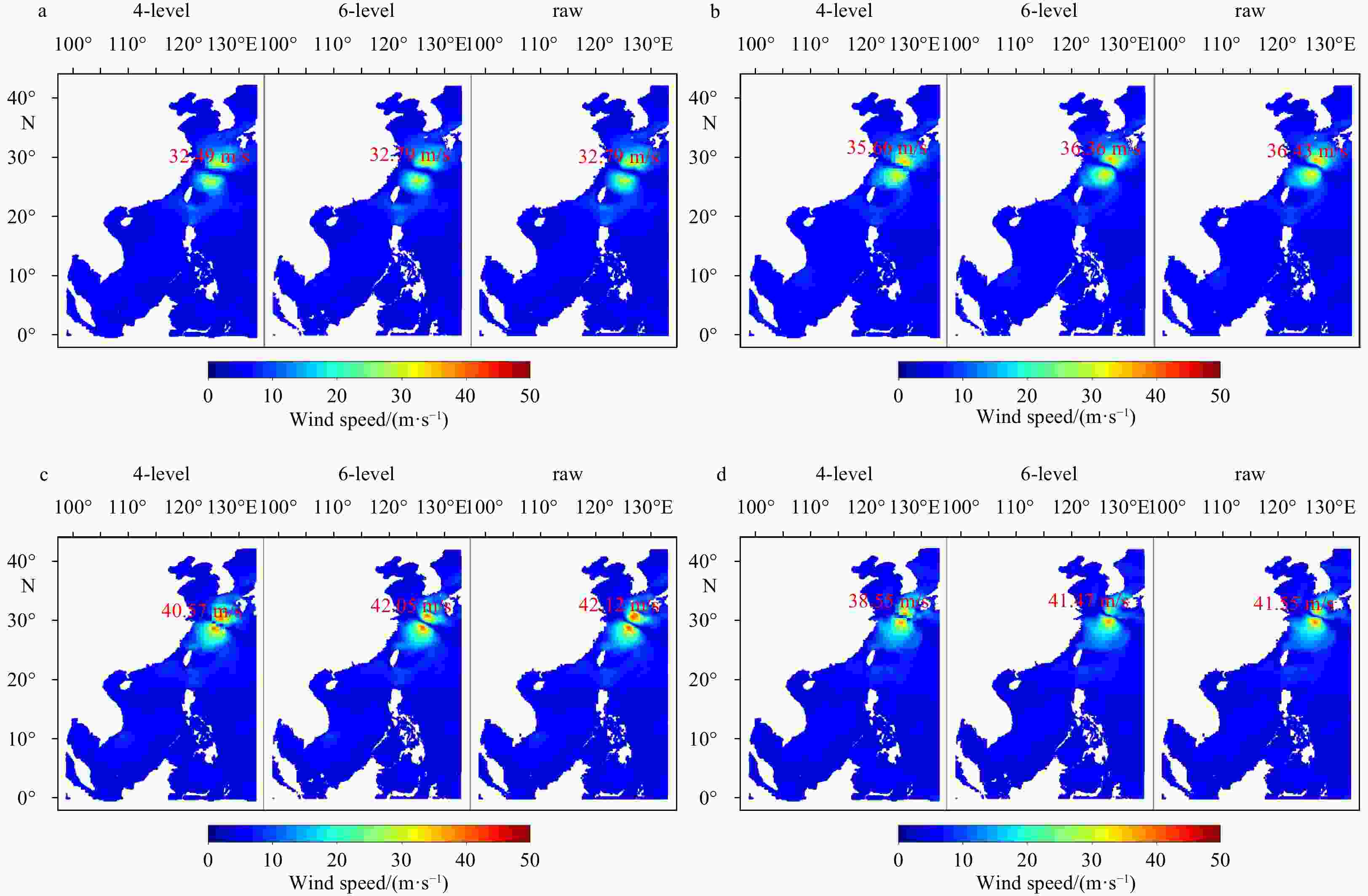
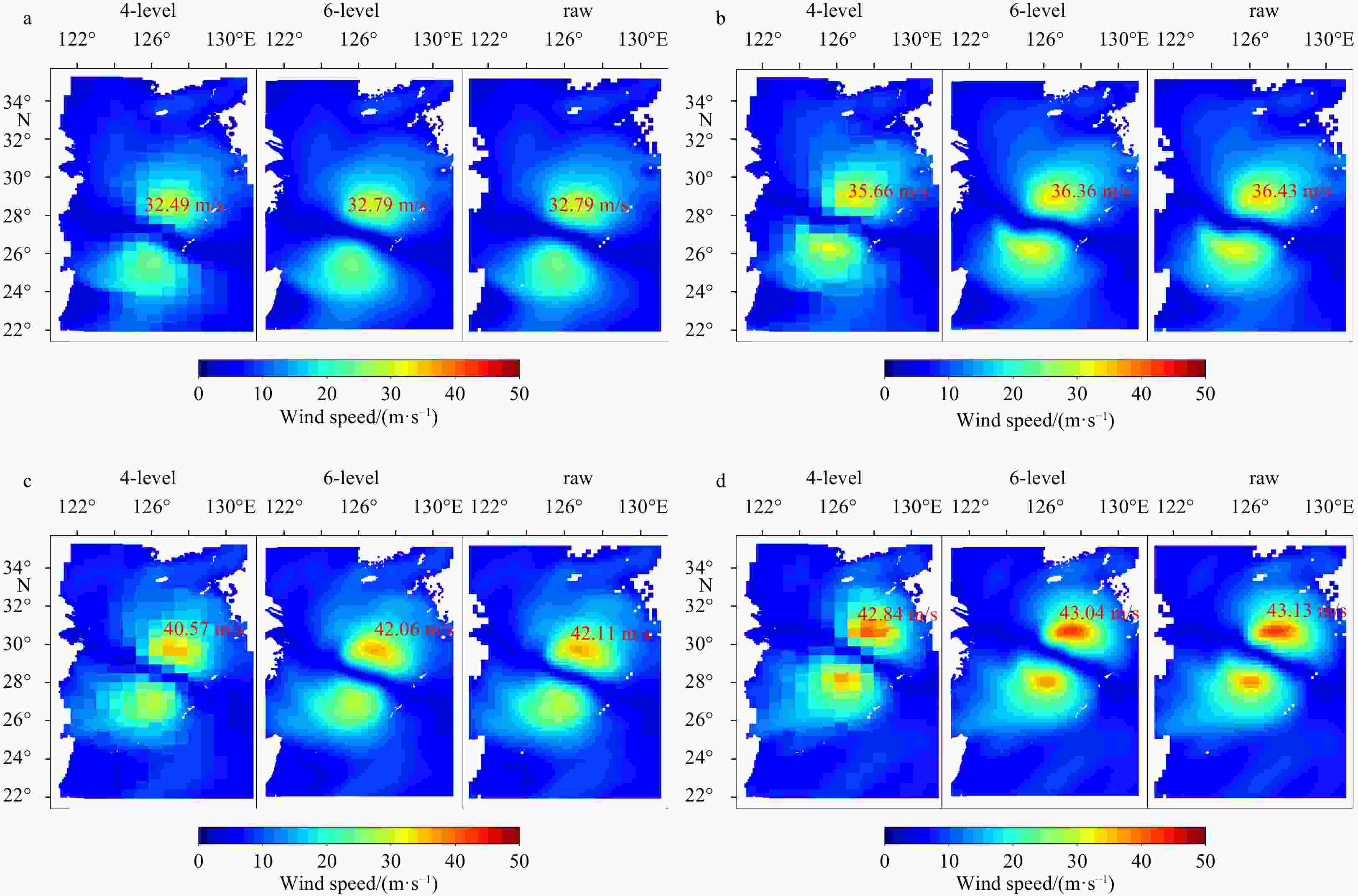
Algorithm Region Resolution 4-level SMC grid nearshore lat: 0.058°, lon: 0.087° nearshore lat: 0.116°, lon: 0.174° nearshore lat: 0.232°, lon: 0.348° open sea lat: 0.464°, lon: 0.696° 6-level SMC grid nearshore (China) lat: 0.014°, lon: 0.021° nearshore (China) lat: 0.028°, lon: 0.042° offshore (China) lat: 0.058°, lon: 0.087° Northwest Pacific lat: 0.116°, lon: 0.174° North Pacific lat: 0.232°, lon: 0.348° global lat: 0.464°, lon: 0.696°
下载: 导出CSV
-
[1] Bunney C, Saulter A. 2015. An ensemble forecast system for prediction of Atlantic–UK wind waves. Ocean Modelling, 96: 103–116. doi: 10.1016/j.ocemod.2015.07.005 [2] Casas-Prat M, Wang X L, Swart N. 2018. CMIP5-based global wave climate projections including the entire Arctic Ocean. Ocean Modelling, 123: 66–85. doi: 10.1016/j.ocemod.2017.12.003 [3] Chawla A, Tolman H L, Gerald V, et al. 2013. A multigrid wave forecasting model: A new paradigm in operational wave forecasting. Weather and Forecasting, 28(4): 1057–1078. doi: 10.1175/WAF-D-12-00007.1 [4] Hsu T W, Ou S H, Liau J M. 2005. Hindcasting nearshore wind waves using a FEM code for SWAN. Coastal Engineering, 52(2): 177–195. doi: 10.1016/j.coastaleng.2004.11.005 [5] Li Jianguo. 2008. Upstream nonoscillatory advection schemes. Monthly Weather Review, 136(12): 4709–4729. doi: 10.1175/2008MWR2451.1 [6] Li Jianguo. 2011. Global transport on a spherical multiple-cell grid. Monthly Weather Review, 139(5): 1536–1555. doi: 10.1175/2010MWR3196.1 [7] Li Jianguo. 2012. Propagation of ocean surface waves on a spherical multiple-cell grid. Journal of Computational Physics, 231(24): 8262–8277. doi: 10.1016/j.jcp.2012.08.007 [8] Li Jingkai, Ma Yunrui, Liu Qingxiang, et al. 2019. Growth of wave height with retreating ice cover in the Arctic. Cold Regions Science and Technology, 164: 102790. doi: 10.1016/j.coldregions.2019.102790 [9] Li Jianguo, Saulter A. 2014. Unified global and regional wave model on a multi-resolution grid. Ocean Dynamics, 64(11): 1657–1670. doi: 10.1007/s10236-014-0774-x [10] Popinet S, Gorman R M, Rickard G J, et al. 2010. A quadtree-adaptive spectral wave model. Ocean Modelling, 34(1/2): 36–49. doi: 10.1016/j.ocemod.2010.04.003 [11] Qi Jianhua, Chen Changsheng, Beardsley R C, et al. 2009. An unstructured-grid finite-volume surface wave model (FVCOM-SWAVE): Implementation, validations and applications. Ocean Modelling, 28(1–3): 153–166. doi: 10.1016/j.ocemod.2009.01.007 [12] Rasch P J. 1994. Conservative shape-preserving two-dimensional transport on a spherical reduced grid. Monthly Weather Review, 122(6): 1337–1350. doi: 10.1175/1520-0493(1994)122<1337:CSPTDT>2.0.CO;2 -
点击查看大图
计量
- 文章访问数: 435
- HTML全文浏览量: 87
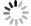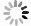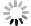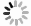
- PDF下载量: 21
- 被引次数: 0
