Modeling calving process of glacier with dilated polyhedral discrete element method
-
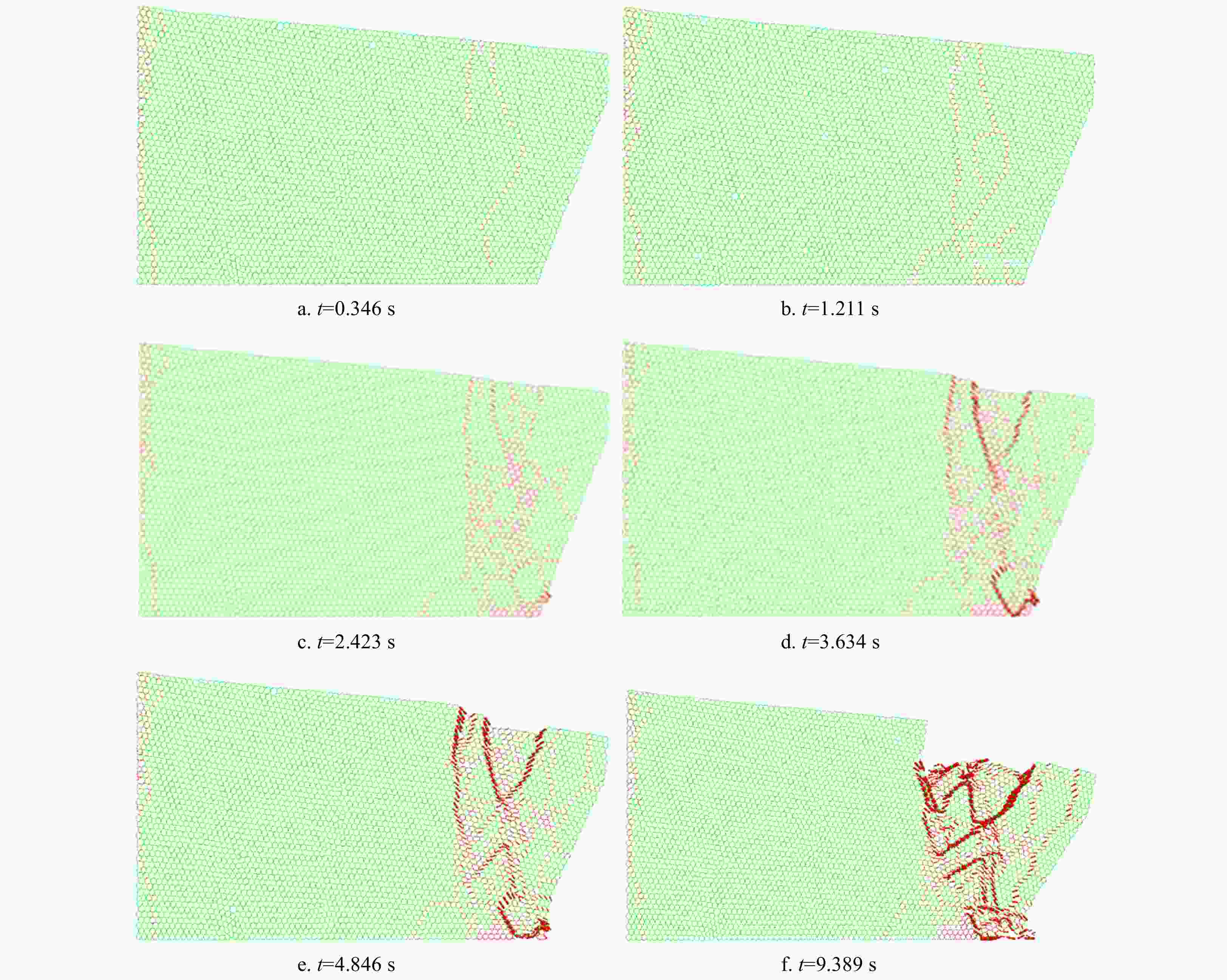
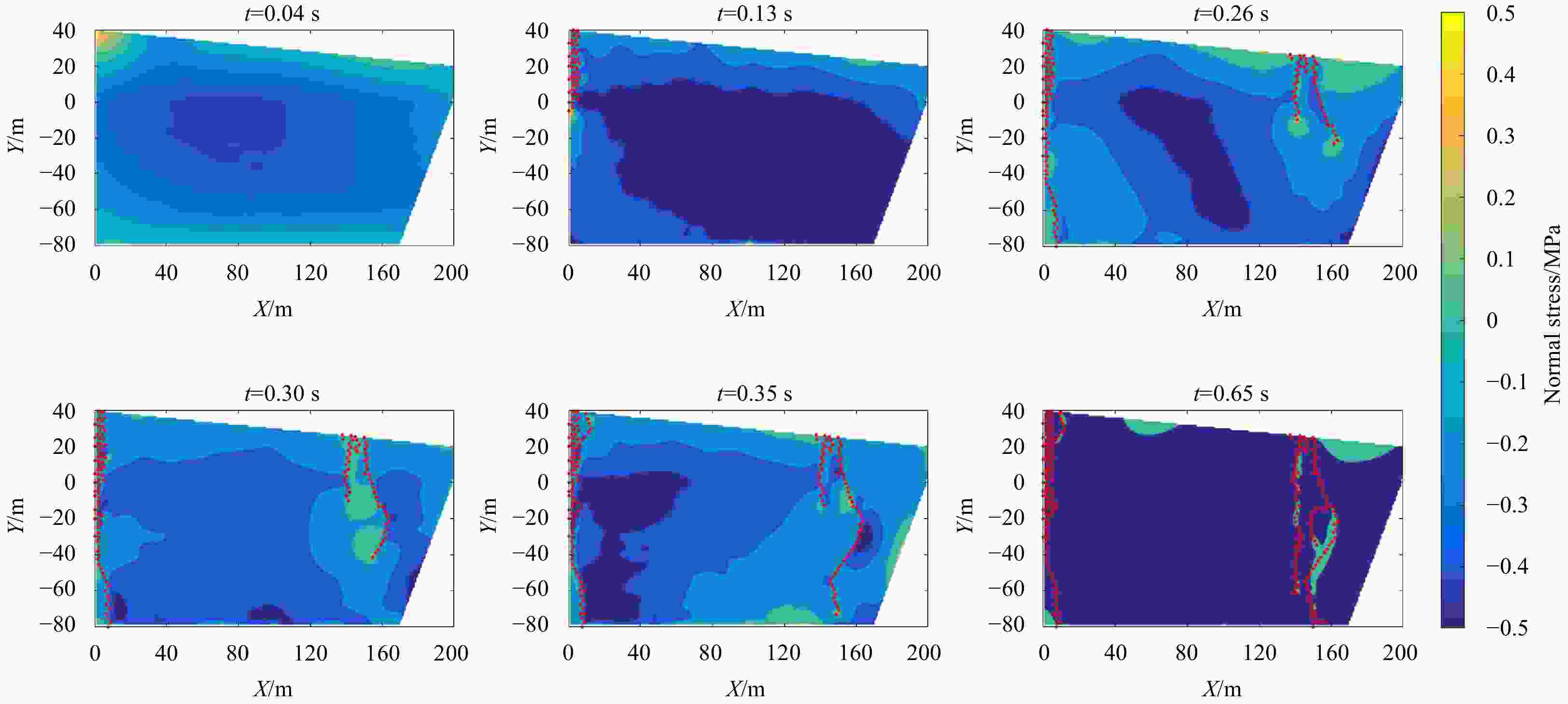
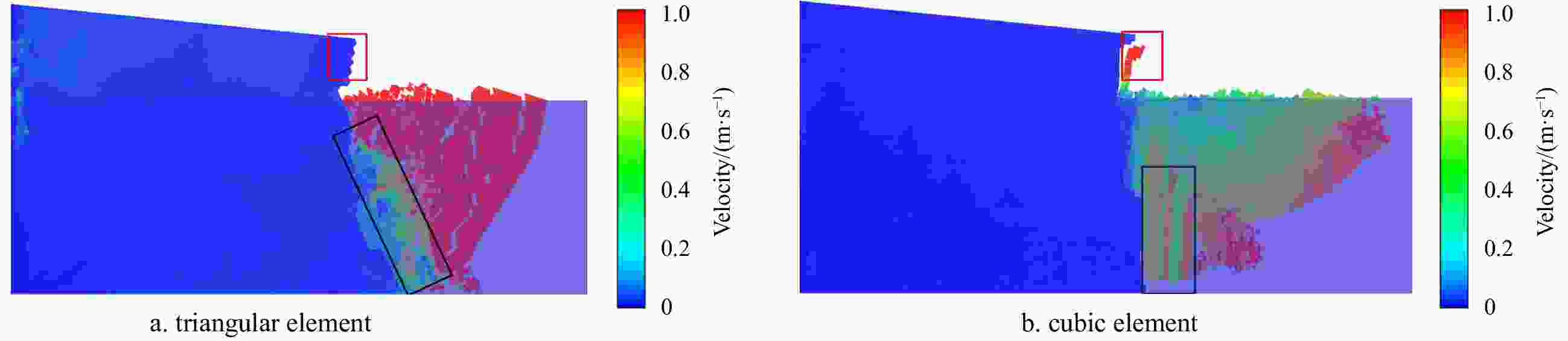
Abstract: Mass loss caused by glacier calving is one of the direct contributors to global sea level rise. Reliable calving laws are required for accurate modelling of ice sheet mass balance. Both continuous and discontinuous methods have been used for glacial calving simulations. In this study, the discrete element method (DEM) based on dilated polyhedral elements is introduced to simulate the calving process of a tidewater glacier. Dilated polyhedrons can be obtained from the Minkowski sum of a sphere and a core polyhedron. These elements can be utilized to generate a continuum ice material, where the interaction force between adjacent elements is modeled by constructing bonds at the joints of the common faces. A hybrid fracture model considering fracture energy is introduced. The viscous creep behavior of glaciers on long-term scales is not considered. By applying buoyancy and gravity to the modelled glacier, DEM results show that the calving process is caused by cracks which are initialized at the top of the glacier and spread to the bottom. The results demonstrate the feasibility of using the dilated polyhedral DEM method in glacier simulations, additionally allowing the fragment size of the breaking fragments to be counted. The relationship between crack propagation and internal stress in the glacier is analyzed during calving process. Through the analysis of the Mises stress and the normal stress between the elements, it is found that geometric changes caused by the glacier calving lead to the redistribution of the stress. The tensile stress between the elements is the main influencing factor of glacier ice failure. In addition, the element shape, glacier base friction and buoyancy are studied, the results show that the glacier model based on the dilated polyhedral DEM is sensitive to the above conditions.
-
Table 1. Main parameters in DPDEM simulation of glacier calving
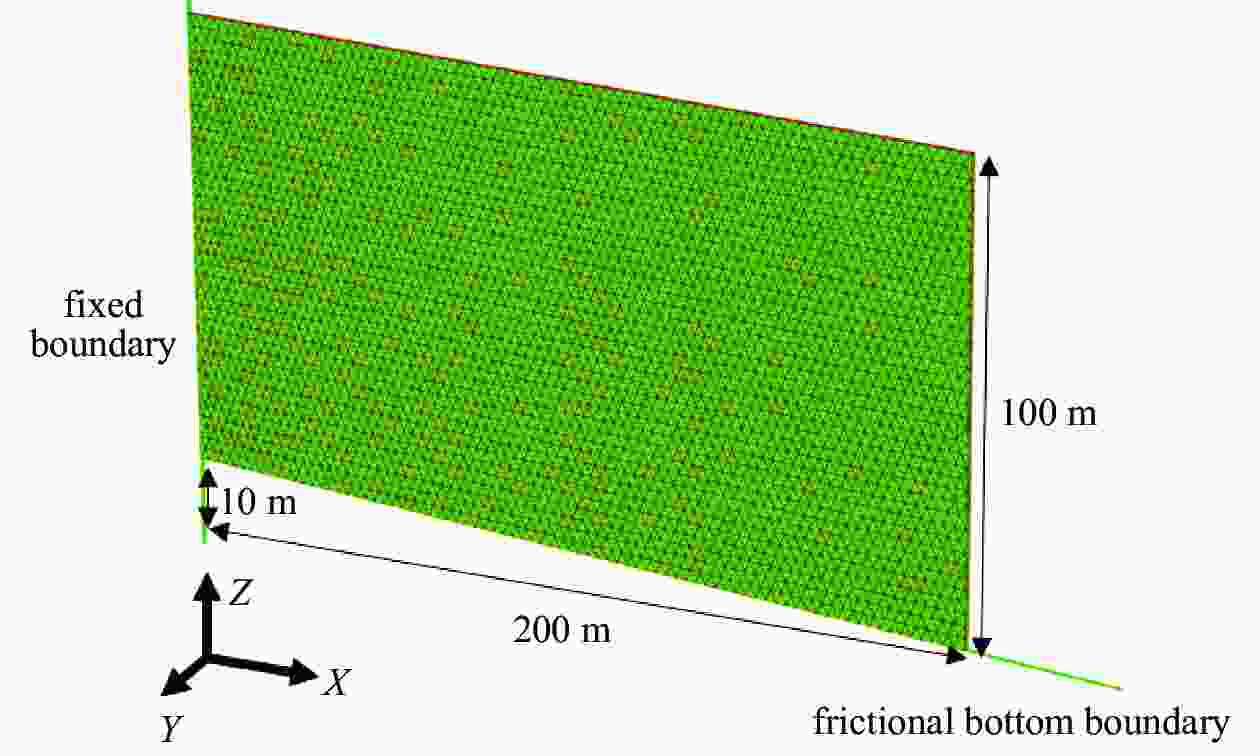
Definition Symbol Value Unit Drag force coefficient $ {C_{{\rm{dF}}}} $ 0.2 1 Drag moment coefficient $ {C_{{\rm{dM}}}} $ 0.14 1 Ice density $ {\rho _{{\rm{ice}}}} $ 1000 kg/m3 Young's modulus $ E $ 10 GPa Poisson’s ratio $ \nu $ 0.3 1 Average element size $ {A_{{\rm{ave}}}} $ 2.5 m2 Element friction coefficient $ \mu $ 0.3 1 Boundary friction coefficient $ {\mu }_{\rm{b}} $ 0.0 1 Under-cut length $L_{\rm{U}}$ 30 m Flotation depth $D_{\rm{F}}$ 20 m Water depth $D_{\rm{ W } }$ 80 m Glacier size $ H\times L $ 120×200 m×m Mode-I fracture energy $ G_{\rm{I}}^c $ 20 N/m Mode-II fracture energy $ G_{{\rm{II}}}^c $ 40 N/m Power coef. for fracture energy η 1.75 1 -
[1] Alley R B, Horgan H J, Joughin I, et al. 2008. A simple law for ice-shelf calving. Science, 322(5906): 1344. doi: 10.1126/science.1162543 [2] Åström J A, Riikilä T I, Tallinen T, et al. 2013. A particle based simulation model for glacier dynamics. The Cryosphere, 7(5): 1591–1602. doi: 10.5194/tc-7-1591-2013 [3] Åström J A, Vallot D, Schäfer M, et al. 2014. Termini of calving glaciers as self-organized critical systems. Nature Geoscience, 7(12): 874–878. doi: 10.1038/ngeo2290 [4] Azevedo N M, Lemos J V. 2005. A generalized rigid particle contact model for fracture analysis. International Journal for Numerical and Analytical Methods in Geomechanics, 29(3): 269–285. doi: 10.1002/nag.414 [5] Bartholomaus T C, Larsen C F, O’ Neel S. 2013. Does calving matter? Evidence for significant submarine melt. Earth and Planetary Science Letters, 380: 21–30. doi: 10.1016/j.jpgl.2013.08.014 [6] Bassis J N, Jacobs S. 2013. Diverse calving patterns linked to glacier geometry. Nature Geoscience, 6(10): 833–836. doi: 10.1038/ngeo1887 [7] Benn D I, Åström J A. 2018. Calving glaciers and ice shelves. Advances in Physics: X, 3(1): 1513819. doi: 10.1080/23746149.2018.1513819 [8] Benn D I, Åström J, Zwinger T, et al. 2017. Melt-under-cutting and buoyancy-driven calving from tidewater glaciers: new insights from discrete element and continuum model simulations. Journal of Glaciology, 63(240): 691–702. doi: 10.1017/jog.2017.41 [9] Benn D I, Warren C R, Mottram R H. 2007. Calving processes and the dynamics of calving glaciers. Earth-Science Reviews, 82(3–4): 143–179. doi: 10.1016/j.earscirev.2007.02.002 [10] Burton J C, Amundson J M, Cassotto R, et al. 2018. Quantifying flow and stress in ice mélange, the world's largest granular material. Proceedings of the National Academy of Sciences of the United States of America, 115(20): 5105–5110. doi: 10.1073/pnas.1715136115 [11] Camanho P P, Davila C G, de Moura M F. 2003. Numerical simulation of mixed-mode progressive delamination in composite materials. Journal of Composite Materials, 37(16): 1415–1438. doi: 10.1177/0021998303034505 [12] Cleary P W. 2010. DEM prediction of industrial and geophysical particle flows. Particuology, 8(2): 106–118. doi: 10.1016/j.partic.2009.05.006 [13] Cook S, Åström J, Zwinger T, et al. 2018. Modelled fracture and calving on the Totten Ice Shelf. The Cryosphere, 12(7): 2401–2411. doi: 10.5194/tc-12-2401-2018 [14] Cundall P A, Strack O D L. 1979. A discrete numerical model for granular assemblies. Géotechnique, 29(1): 47–65 [15] Dempsey J P, Adamson R M, Mulmule S V. 1999. Scale effects on the in-situ tensile strength and fracture of ice. Part II: First-year sea ice at Resolute, NWT. International Journal of Fracture, 95(1): 347–366. doi: 10.1023/A:1018650303385 [16] Dyer M S, Collins C, Hodgeman D, et al. 2013. Computationally assisted identification of functional inorganic materials. Science, 340(6134): 847–852. doi: 10.1126/science.1226558 [17] Golledge N R, Keller E D, Gomez N, et al. 2019. Global environmental consequences of twenty-first-century ice-sheet melt. Nature, 566(7742): 65–72. doi: 10.1038/s41586-019-0889-9 [18] Gürtner A, Bjerkås M, Forsberg J, et al. 2010. Numerical modelling of a full scale ice event. In: 20th IAHR International Symposium on Ice. Lahti, Finland: IAHR [19] Koehn D, Sachau T. 2014. Two-dimensional numerical modeling of fracturing and shear band development in glacier fronts. Journal of Structural Geology, 61: 133–142. doi: 10.1016/j.jsg.2012.11.002 [20] Liu Lu, Ji Shunying. 2018. Ice load on floating structure simulated with dilated polyhedral discrete element method in broken ice field. Applied Ocean Research, 75: 53–65. doi: 10.1016/j.apor.2018.02.022 [21] Liu Lu, Ji Shunying. 2019. Bond and fracture model in dilated polyhedral DEM and its application to simulate breakage of brittle materials. Granular Matter, 21(3): 41. doi: 10.1007/s10035-019-0896-4 [22] Lu W, Lubbad R, Løset S. 2014. Simulating ice-sloping structure interactions with the cohesive element method. Journal of Offshore Mechanics & Arctic Engineering, 136(3): 16. doi: 10.1115/1.4026959 [23] Lu G, Third J R, Müller C R. 2015. Discrete element models for non-spherical particle systems: from theoretical developments to applications. Chemical Engineering Science, 127: 425–465. doi: 10.1016/j.ces.2014.11.050 [24] Ma Gang, Zhou Wei, Chang Xiaolin, et al. 2016. A hybrid approach for modeling of breakable granular materials using combined finite-discrete element method. Granular Matter, 18: 7. doi: 10.1007/s10035-016-0615-3 [25] Ma Yue, Tripathy C S, Bassis J N. 2017. Bounds on the calving cliff height of marine terminating glaciers. Geophysical Research Letters, 44(3): 1369–1375. doi: 10.1002/2016GL071560 [26] Mercenier R, Lüthi M P, Vieli A. 2018. Calving relation for tidewater glaciers based on detailed stress field analysis. The Cryosphere, 12(2): 721–739. doi: 10.5194/tc-12-721-2018 [27] Paavilainen J, Tuhkuri J. 2012. Parameter effects on simulated ice rubbling forces on a wide sloping structure. Cold Regions Science and Technology, 81: 1–10. doi: 10.1016/j.coldregions.2012.04.005 [28] Paavilainen J, Tuhkuri J, Polojärvi A. 2011. 2D numerical simulations of ice rubble formation process against an inclined structure. Cold Regions Science and Technology, 68(1−2): 20–34. doi: 10.1016/j.coldregions.2011.05.003 [29] Pelto M S, Warren C R. 1991. Relationship between tidewater glacier calving velocity and water depth at the calving front. Annals of Glaciology, 15: 115–118. doi: 10.3189/S0260305500009617 [30] Pralong A, Funk M. 2005. Dynamic damage model of crevasse opening and application to glacier calving. Journal of Geophysical Research: Solid Earth, 110(B1): B01309. doi: 10.1029/2004JB003104 [31] Riikilä T I, Tallinen T, Åström J, et al. 2015. A discrete-element model for viscoelastic deformation and fracture of glacial ice. Computer Physics Communications, 195: 14–22. doi: 10.1016/j.cpc.2015.04.009 [32] Robel A A. 2017. Thinning sea ice weakens buttressing force of iceberg mélange and promotes calving. Nature Communications, 8(1): 14596. doi: 10.1038/ncomms14596 [33] Rothrock D A, Thorndike A S. 1984. Measuring the sea ice floe size distribution. Journal of Geophysical Research: Oceans, 89(C4): 6477–6486. doi: 10.1029/JC089iC04p06477 [34] Savage S B, Crocker G B, Sayed M, et al. 2000. Size distributions of small ice pieces calved from icebergs. Cold Regions Science and Technology, 31(2): 163–172. doi: 10.1016/S0165-232X(00)00010-0 [35] Schlemm T, Levermann A. 2018. A simple stress-based cliff-calving law. The Cryosphere, 13: 2475–2488. doi: 10.5194/tc-13-2475-2019 [36] Todd J, Christoffersen P, Zwinger T, et al. 2018. A full-stokes 3-D calving model applied to a large greenlandic glacier. Journal of Geophysical Research: Earth Surface, 123(3): 410–432. doi: 10.1002/2017JF004349 [37] van Dongen E C H, Kirchner N, van Gijzen M B, et al. 2018. Dynamically coupling full Stokes and shallow shelf approximation for marine ice sheet flow using Elmer/Ice (v8.3). Geoscientific Model Development, 11(11): 4563–4576. doi: 10.5194/gmd-11-4563-2018 [38] Zemp M, Huss M, Thibert E, et al. 2019. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature, 568(7752): 382–386. doi: 10.1038/s41586-019-1071-0 -



 下载:
下载: